Playing with Numbers Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Numbers are like the building blocks of mathematics, and exploring them is like embarking on a treasure hunt! In this exciting chapter, we dive into the world of numbers to uncover their secrets—how they can be grouped, divided, multiplied, and related to each other in fascinating ways. From simplifying expressions with brackets to finding factors, multiples, and prime numbers, this chapter is all about playing with numbers to discover their hidden patterns and properties. We’ll also learn cool tricks like the Sieve of Eratosthenes to spot prime numbers and explore how to find the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) to solve real-world problems. Get ready to have fun with numbers as we break them down and build them up in creative ways!

Simplification of Brackets
- Brackets are symbols used to group parts of an expression, such as -, (), {}, [], and <>.
- To simplify an expression with brackets, start with the innermost bracket and work outward.
Steps to simplify brackets:
- Identify the innermost bracket and solve the expression inside it first.
- Perform operations like addition, subtraction, multiplication, or division within the bracket.
- Replace the bracket with the result and move to the next bracket, repeating until all brackets are removed.
- Complete any remaining operations in the expression.
Example: Simplify: 45 - [30 - {18 + (2 × (9 ÷ 3))}].
- Start with the innermost bracket (9 ÷ 3) = 3.
- Now solve (2 × 3) = 6.
- Next, solve {18 + 6} = 24.
- Then, solve [30 - 24] = 6.
- Finally, solve 45 - 6 = 39.
- Answer: 39
Factors
- A factor is a number that divides another number completely without leaving a remainder.
- When numbers are multiplied, each number is a factor of the product.
Steps to find factors:
- Write the number as a product of two numbers in all possible ways.
- List all numbers that appear in these products.
Properties of factors:
- 1 is a factor of every number.
- Every number is a factor of itself.
- A factor divides a number exactly.
- A factor is less than or equal to the number.
- Factors of a number are finite.
Example: Find all the factors of 18.
- Write 18 as products: 1 × 18, 2 × 9, 3 × 6.
- The factors are 1, 2, 3, 6, 9, and 18.
Multiples
- A multiple is obtained by multiplying a number by a natural number (1, 2, 3, ...).
- Multiples of a number are infinite because you can keep multiplying by larger natural numbers.
Steps to find multiples:
- Multiply the number by 1, 2, 3, and so on.
- List the results as multiples.
Properties of multiples:
- A multiple is greater than or equal to the number.
- Every number is a multiple of 1 and itself.
- Multiples of a number are infinite.
Example: Find all multiples of 13 up to 100.
- Multiply 13 by natural numbers: 13 × 1 = 13, 13 × 2 = 26, 13 × 3 = 39, 13 × 4 = 52, 13 × 5 = 65, 13 × 6 = 78, 13 × 7 = 91.
- Multiples are 13, 26, 39, 52, 65, 78, 91.
Types of Numbers
Even Numbers
- Numbers divisible by 2 are even numbers.
- Example: 0, 2, 4, 6, 8, etc.
Odd Numbers
- Numbers not divisible by 2 are odd numbers.
- Example: 1, 3, 5, 7, 9, etc.
Prime Numbers
- Numbers greater than 1 with only two factors (1 and itself) are prime numbers.
- Example: 2, 3, 5, 7, 11, 13, etc.
Composite Numbers
- Numbers with more than two factors are composite numbers.
- Example: 4, 6, 8, 9, 10, etc.
Maths Info
- The smallest prime number is 2.
- The only even prime number is 2.
- 1 is neither prime nor composite.
Example
Write the prime and composite numbers less than 15.
- Prime numbers: 2, 3, 5, 7, 11, 13 (only 1 and themselves as factors).
- Composite numbers: 4, 6, 8, 9, 10, 12, 14 (more than two factors).
Sieve of Eratosthenes
A method to find prime numbers from 1 to 100.
Steps:
- Write numbers from 1 to 100 in rows of 10.
- Cross out 1 (not prime).
- Encircle 2 (smallest prime) and cross out all multiples of 2.
- Encircle 3 and cross out its multiples.
- Continue with the next uncrossed number until all numbers are either encircled (prime) or crossed out (composite, except 1).
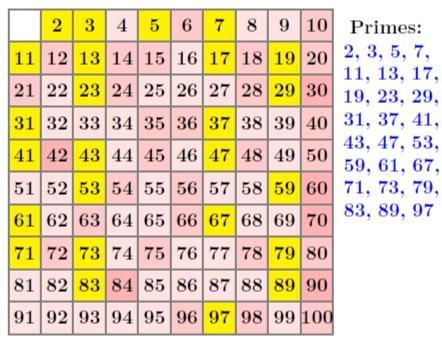
Example: Using the Sieve of Eratosthenes, numbers like 2, 3, 5, 7, 11, etc., are coloured as primes, while 4, 6, 8, 9, etc., are not coloured as composites.
Divisibility Tests
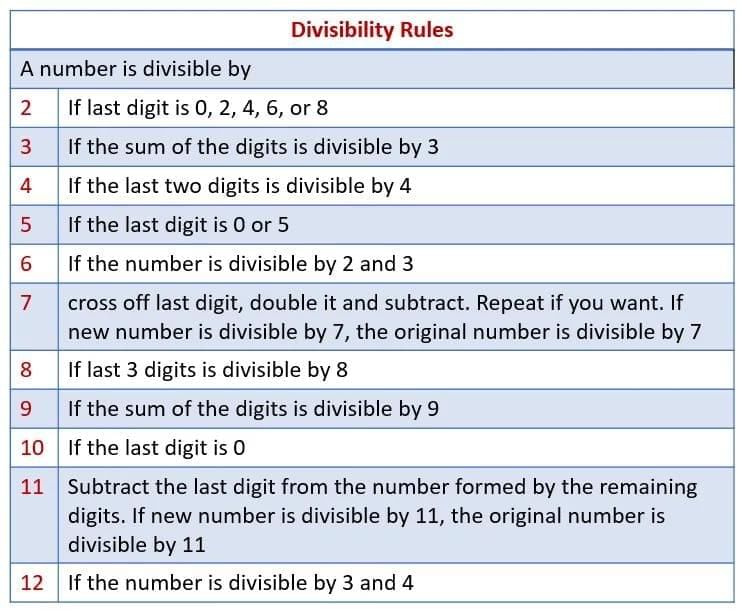
Example: is 738 divisible by 3?
Solution:
Rule for 3: Sum of digits should be divisible by 3.
Sum of digits = 7 + 3 + 8 = 18
18 ÷ 3 = 6 (exact division)
So, 738 is divisible by 3.
Example: Is 2450 divisible by 5?
Solution:
Rule for 5: Last digit should be 0 or 5.
Last digit = 0
So, 2450 is divisible by 5.
Example: Is 7324 divisible by 4?
Solution:
Rule for 4: Check last two digits.
Last two digits = 24
24 ÷ 4 = 6 (exact division)
So, 7324 is divisible by 4.
Example: Is 180 divisible by 6?
Solution:
Rule for 6: Number should be divisible by both 2 and 3.
180 ends with 0 (even) → divisible by 2.
Sum of digits = 1 + 8 + 0 = 9 → divisible by 3.
So, 180 is divisible by 6.
Example: Is 123456 divisible by 9?
Solution:
Rule for 9: Sum of digits should be divisible by 9.
Sum of digits = 1+2+3+4+5+6 = 21
21 ÷ 9 = 2.33 (not exact)
So, 123456 is not divisible by 9.
Example: Is 372 divisible by 11?
Solution:
Rule for 11: Difference between sum of digits at odd and even places.
Odd places: 3 (1st) + 2 (3rd) = 5
Even place: 7 (2nd)
Difference = 5 - 7 = -2
-2 is not divisible by 11.
So, 372 is not divisible by 11.
Common Factors
A common factor divides two or more numbers completely.
Steps to find common factors:
- List all factors of each number.
- Identify factors common to all numbers.
Example: Find common factors of 15 and 18.
- Factors of 15: 1, 3, 5, 15.
- Factors of 18: 1, 2, 3, 6, 9, 18.
- Common factors: 1, 3.
Common Multiples
A common multiple is divisible by two or more numbers.
Steps to find common multiples:
- List multiples of each number.
- Identify numbers common to all lists.
Example: Find common multiples of 15 and 18.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, …
- Multiples of 18: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, …
- Common multiples: 90, 180, …
Co-prime Numbers
- Two numbers with only 1 as their common factor are co-prime.
- Prime number pairs are always co-prime.
- Composite numbers can also be co-prime.
Example: Are 9 and 16 co-prime?
- Factors of 9: 1, 3, 9.
- Factors of 16: 1, 2, 4, 8, 16.
- Common factor: 1.
- Since only 1 is common, 9 and 16 are co-prime.
Prime Factorization
- Expressing a composite number as a product of prime factors.
- According to the Fundamental Theorem of Arithmetic, every composite number has a unique prime factorization.
Steps for prime factorization:
- Divide the number by the smallest prime factor.
- Continue dividing the quotient by prime numbers until the quotient is 1.
- Write the number as a product of these prime factors.
Example: Find the prime factorization of 1,000.
- 1,000 ÷ 2 = 500
- 500 ÷ 2 = 250
- 250 ÷ 2 = 125
- 125 ÷ 5 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
- Prime factorization: 2 × 2 × 2 × 5 × 5 × 5.
Highest Common Factor (HCF)
- The HCF is the largest number that divides two or more numbers completely.
- Also called the Greatest Common Divisor (GCD).
Methods to find HCF:
- Common Factor Method
- Prime Factorization Method
- Division Method
Common Factor Method
Steps:
- List all factors of each number.
- Identify common factors.
- Select the largest common factor as the HCF.
Example: Find the HCF of 30, 24, and 48.
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24.
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
- Common factors: 1, 2, 3, 6.
- HCF: 6.
Prime Factorization Method
Steps:
- Find prime factors of each number.
- Identify common prime factors.
- Multiply the common prime factors to get the HCF.
Example: Find the HCF of 50, 80, and 150.
- 50 = 2 × 5 × 5.
- 80 = 2 × 2 × 2 × 2 × 5.
- 150 = 2 × 3 × 5 × 5.
- Common prime factors: 2, 5.
- HCF = 2 × 5 = 10.
Division Method
Steps for two numbers:
- Divide the larger number by the smaller number.
- If the remainder is 0, the smaller number is the HCF.
- If there’s a remainder, divide the previous divisor by the remainder.
- Repeat until the remainder is 0; the last divisor is the HCF.
Steps for more than two numbers:
- Find the HCF of any two numbers.
- Find the HCF of the result and the next number.
- Continue until all numbers are processed.
Example: Find the HCF of 240 and 340.
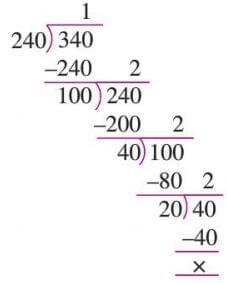
- 340 ÷ 240 = 1, remainder 100.
- 240 ÷ 100 = 2, remainder 40.
- 100 ÷ 40 = 2, remainder 20.
- 40 ÷ 20 = 2, remainder 0.
- HCF = 20.
Lowest Common Multiple (LCM)
The LCM is the smallest number divisible by two or more numbers.
Methods to find LCM:
- Common Multiple Method
- Prime Factorization Method
- Division Method
Maths Info: The LCM of prime numbers is their product.
Common Multiple Method
Steps:
- List multiples of each number.
- Identify common multiples.
- Select the smallest common multiple as the LCM.
Example: Find the LCM of 4, 5, and 20.
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 5: 5, 10, 15, 20, 25, …
- Multiples of 20: 20, 40, 60, …
- Common multiples: 20, 40, 60, …
- LCM: 20.
Prime Factorization Method
Steps:
- Find prime factors of each number.
- Take each prime factor with the highest power it appears in any number.
- Multiply these to get the LCM.
Example: Find the LCM of 16, 96, and 448.
- 16 = 24.
- 96 = 25 × 3.
- 448 = 26 × 7.
- Highest powers: 26, 3, 7.
- LCM = 26 × 3 × 7 = 64 × 3 × 7 = 1,344.
Division Method
Steps:
- Write numbers in a row, separated by commas.
- Divide by a prime number that divides at least two numbers.
- Write quotients below and carry over non-divisible numbers.
- Repeat until no two numbers share a common factor.
- Multiply all divisors and remaining quotients to get the LCM.
Example: Find the LCM of 42, 70, and 210.
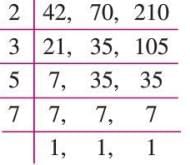
- LCM = 2 × 3 × 5 × 7 = 210.
Relation between HCF and LCM of Two Numbers
Formula: HCF × LCM = Product of the two numbers.
Derived formulas:
- HCF = (Product of the two numbers) ÷ LCM
- LCM = (Product of the two numbers) ÷ HCF
- (HCF × LCM) ÷ One number = Other number
LCM of co-prime numbers is their product since their HCF is 1.
Example: Verify the relation for 75 and 135.
- Prime factors: 75 = 3 × 5 × 5, 135 = 3 × 3 × 3 × 5.
- HCF = 3 × 5 = 15.
- LCM = 33 × 52 = 27 × 25 = 675.
- HCF × LCM = 15 × 675 = 10,125.
- Product of numbers = 75 × 135 = 10,125.
- Since 15 × 675 = 75 × 135, the relation is verified.
Solved Examples
Example 1: Check if 15 is a factor of 315.
- Divide 315 by 15: 315 ÷ 15 = 21, remainder 0.
- Since the remainder is 0, 15 is a factor of 315.
Example 2: Express 44 as the sum of two odd prime numbers.
- Try pairs of odd primes: 13 + 31 = 44.
- Answer: 44 = 13 + 31.
Example 3: Find the HCF of 250 and 930 using the division method.
- Find the HCF of 250 and 930:

Thus, the HCF of 250 and 930 = 10. Now, find the HCF of 10 and 445.
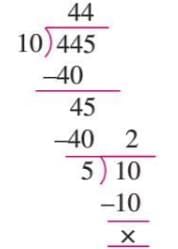
HCF of 10 and 445 is 5.
Thus, the HCF of 250, 930, and 445 is 5.
Example 4: Find the smallest number divisible by 24, 54, 25, and 75.
- Use the division method:
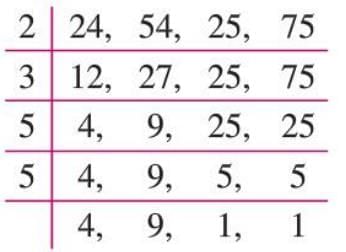
- LCM = 2 × 3 × 5 × 5 × 4 × 9 = 5,400.
|
44 videos|202 docs|24 tests
|
FAQs on Playing with Numbers Chapter Notes - Mathematics Class 6 ICSE
| 1. What is the significance of simplifying brackets in mathematical expressions? |  |
| 2. How can I find the factors and multiples of a number? |  |
| 3. What are co-prime numbers and how can they be identified? |  |
| 4. What is the Sieve of Eratosthenes, and how does it work? |  |
| 5. How can I perform divisibility tests for various numbers? |  |
















