Fractions Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Imagine you have a delicious chocolate bar, and you want to share it with your friends. If you break it into equal pieces, each piece is a fraction of the whole bar! Fractions are all about dividing things into parts and understanding how those parts relate to the whole. Whether it's sharing a pizza, measuring ingredients for a cake, or even figuring out how much of a book you've read, fractions are everywhere in our daily lives. In this chapter, we'll dive into the exciting world of fractions, learning how to work with them, compare them, and even use them to solve fun problems. Get ready to slice up some knowledge!

Fraction as Division
- A fraction shows division, where the numerator is divided by the denominator.
- Every fraction can be written as a division, and every division can be written as a fraction.
- Formula: a/b = a ÷ b
- Steps to Understand:
- Take a whole object and divide it into equal parts.
- The number of parts you take out of the total parts forms a fraction.
- This fraction represents the division of the parts by the total parts.
- Example: Two wholes are divided into 6 equal parts. Each part is 2 ÷ 6 = 2/6. So, 2/6 represents the fraction of one part.
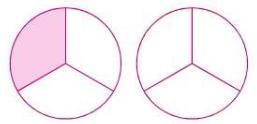
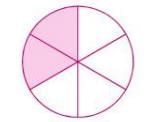
Types of Fractions
Proper Fractions
- Fractions where the numerator is less than the denominator.
- They represent a value less than 1.
- Steps to Identify:
- Check the numerator and denominator.
- If the numerator < denominator, it’s a proper fraction.
- Example: 6/19 is a proper fraction because 6 < 19.
Improper Fractions
- Fractions where the numerator is greater than or equal to the denominator.
- They represent a value equal to or more than 1.
- Steps to Identify:
- Compare the numerator and denominator.
- If numerator ≥ denominator, it’s an improper fraction.
- Example: 9/8 is an improper fraction because 9 > 8.
Mixed Fractions
- Consist of a whole number and a proper fraction combined.
- The whole number is called the whole part, and the fraction is the fractional part.
- Steps to Understand:
- Identify the whole number.
- Identify the proper fraction attached to it.
- Example: 56/7 is a mixed fraction with 5 as the whole part and 6/7 as the fractional part.
Equivalent Fractions
- Fractions that represent the same value but look different.
- Obtained by multiplying or dividing both numerator and denominator by the same positive number.
- Steps to Find:
- Choose a fraction.
- Multiply or divide both numerator and denominator by the same number.
- The new fraction is equivalent to the original.
- Example: To find an equivalent fraction of 1/2 with a numerator of 2, 4 and 8. The fractions 1/2, 2/4, 4/8 and 5/10 are equivalent fractions.

Like and Unlike Fractions
- Like Fractions: Fractions with the same denominator.
- Unlike Fractions: Fractions with different denominators.
- Steps to Differentiate:
- Look at the denominators of the fractions.
- If they are the same, they are like fractions; if different, they are unlike fractions.
- Example: 21/25 and 14/25 are like fractions (same denominator 25), while 7/8 and 7/17 are unlike fractions (different denominators 8 and 17).
Reducing a Fraction to Its Lowest Terms
A fraction is in its simplest form if the numerator and denominator have no common factor except 1.
Two methods to reduce fractions:
- Prime Factorization Method:
- Write numerator and denominator as products of prime factors.
- Cancel common factors.
- The result is the fraction in lowest terms.
- Example: For 18/48, prime factors are
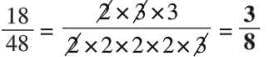
- HCF Method:
- Find the Highest Common Factor (HCF) of numerator and denominator.
- Divide both numerator and denominator by the HCF.
- Example: For 36/144, the HCF is 36. Divide both by 36: 36/144 = (36 ÷ 36)/(144 ÷ 36) = 1/4.
Conversion of Fractions
Conversion of Mixed Fractions into Improper Fractions
- Converts a mixed fraction into an improper fraction using a formula.
- Formula:
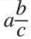 = (a × c + b)/c
= (a × c + b)/c - Steps:
- Multiply the whole number (a) by the denominator (c).
- Add the numerator (b) to the result.
- Place the sum over the original denominator (c).
- Example: Convert
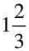 : (1 × 3 + 2)/3 = (3 + 2)/3 = 5/3.
: (1 × 3 + 2)/3 = (3 + 2)/3 = 5/3.
Conversion of Improper Fractions into Mixed Fractions
- Converts an improper fraction into a mixed fraction by division.
- Formula: Improper fraction = QuotientRemainder/Denominator
- Steps:
- Divide the numerator by the denominator to get the quotient and remainder.
- Write the quotient as the whole number.
- Place the remainder over the original denominator as the fractional part.
- Example: Convert 9/4: 9 ÷ 4 gives quotient 2 and remainder 1, so 9/4 =
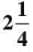 .
.
Conversion of Unlike Fractions into Like Fractions
- Converts unlike fractions into like fractions using the LCM method.
- Steps:
- Find the Least Common Multiple (LCM) of the denominators.
- Divide the LCM by each fraction’s denominator to get the quotient.
- Multiply both numerator and denominator of each fraction by its quotient.
- Example: Convert 5/7 and 7/8 into like fractions.
LCM of 7 and 8 is 56.
For 5/7: (5 × 8)/(7 × 8) = 40/56.
For 7/8: (7 × 7)/(8 × 7) = 49/56.
Representation of Fractions on the Number Line
- Fractions can be shown as points on a number line.
- Steps to Represent a Fraction:
- Mark 0 and 1 on the number line.
- Divide the segment between 0 and 1 into equal parts equal to the denominator.
- Count the parts equal to the numerator to locate the fraction.
- For Mixed Fractions:
- Locate the whole number part on the number line.
- Divide the segment to the next whole number into parts equal to the denominator.
- Mark the fractional part.
- For Improper Fractions: Convert to a mixed fraction first, then follow the steps for mixed fractions.
- Example: To represent 1/5, 3/5, and 9/5:
Divide 0 to 1 into 5 equal parts. The first mark is 1/5, the third is 3/5. For 9/5 = 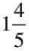 , divide 1 to 2 into 5 parts; the fourth mark is 9/5.
, divide 1 to 2 into 5 parts; the fourth mark is 9/5.

Comparison of Fractions
Comparison of Like Fractions
- Compare fractions with the same denominator by comparing numerators.
- Rules:
- a/c > b/c if a > b
- a/c < b/c if a < b
- a/c = b/c if a = b
- Steps:
- Ensure the denominators are the same.
- Compare the numerators directly.
- Example: Arrange 2/13, 5/13, 9/13, 7/13 in ascending order. Numerators are 2, 5, 9, and 7. So, 2/13 < 5/13 < 7/13 < 9/13.
Comparison of Unlike Fractions
- Convert unlike fractions to like fractions, then compare.
- Steps (LCM Method):
- Find the LCM of the denominators.
- Convert each fraction to have the LCM as the denominator.
- Compare the numerators.
- Alternate Method (Same Numerator):
- Find the LCM of the numerators.
- Convert fractions to have the same numerator using the LCM.
- The fraction with the smallest denominator is the largest.
- Example (LCM Method): Compare 12/15, 9/5, 7/16, 11/20.
LCM of denominators 15, 5, 16, 20 is 240.
Convert: 12/15 = 192/240, 9/5 = 432/240, 7/16 = 105/240, 11/20 = 132/240.
Since 432 > 192 > 132 > 105, order is 9/5 > 12/15 > 11/20 > 7/16.
- Example (Same Numerator): Compare 1/16, 5/4, 2/3, 8/9.
LCM of numerators 1, 5, 2, 8 is 40.
Convert: 1/16 = 40/640, 5/4 = 40/32, 2/3 = 40/60, 8/9 = 40/45.
Since 32 < 45 < 60 < 640, order is 5/4 > 8/9 > 2/3 > 1/16.
Inserting a Fraction between Two Fractions
- Find a fraction between two given fractions a/b and c/d where a/b < c/d.
- Formula: (a + c)/(b + d)
- Steps:
- Add the numerators to get the new numerator.
- Add the denominators to get the new denominator.
- Simplify the resulting fraction if needed.
- Example: Insert a fraction between 2/5 and 6/5.
(2 + 6)/(5 + 5) = 8/10 = 4/5.
So, 2/5 < 4/5 < 6/5.
Fundamental Operations on Fractions
Addition and Subtraction of Like Fractions
- Add or subtract the numerators and keep the denominator the same.
- Reduce the result to the lowest terms if needed.
- Steps:
- Check if denominators are the same.
- Add or subtract the numerators.
- Write the result over the common denominator.
- Simplify if possible.
- Example: Evaluate 3/5 + 7/5
= (3 + 7)/5 = 10/5
= 2.
Addition and Subtraction of Unlike Fractions or Mixed Fractions
- Convert unlike fractions to like fractions, then add or subtract.
- For mixed fractions, convert to improper fractions first, or add/subtract whole and fractional parts separately.
- Steps (Improper Fraction Method):
- Convert mixed fractions to improper fractions.
- Find the LCM of the denominators.
- Convert fractions to have the LCM as the denominator.
- Add or subtract numerators, keeping the denominator.
- Simplify the result.
- Alternate Method (Separate Parts):
- Add or subtract the whole number parts.
- Convert fractional parts to like fractions and add or subtract.
- Combine the results and simplify.
- Example (Improper Fraction): Evaluate
 . Convert:
. Convert: 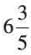 = 33/5,
= 33/5, 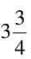 = 15/4. LCM of 5 and 4 is 20. Convert: 33/5 = 132/20, 15/4 = 75/20. Subtract: 132/20 - 75/20 = 57/20 =
= 15/4. LCM of 5 and 4 is 20. Convert: 33/5 = 132/20, 15/4 = 75/20. Subtract: 132/20 - 75/20 = 57/20 = 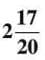 .
. - Example (Alternate Method):
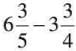 = (6 - 3) + (3/5 - 3/4). Whole part: 6 - 3 = 3. Fractional part: LCM of 5 and 4 is 20, so 3/5 = 12/20, 3/4 = 15/20. Subtract: 12/20 - 15/20 = -3/20. Combine: 3 - 3/20 = 2 + (1 - 3/20) =
= (6 - 3) + (3/5 - 3/4). Whole part: 6 - 3 = 3. Fractional part: LCM of 5 and 4 is 20, so 3/5 = 12/20, 3/4 = 15/20. Subtract: 12/20 - 15/20 = -3/20. Combine: 3 - 3/20 = 2 + (1 - 3/20) =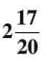 .
.
Multiplication of Fractions
- Multiply numerators to get the new numerator and denominators to get the new denominator.
- Convert mixed fractions to improper fractions first.
- Simplify by canceling common factors before multiplying, if possible.
- Steps:
- Convert any mixed fractions to improper fractions.
- Multiply the numerators together.
- Multiply the denominators together.
- Simplify the resulting fraction.
- Alternate Method (Canceling):
- Factorize numerators and denominators.
- Cancel common factors.
- Multiply the remaining terms.
- Example: Multiply
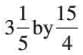 .
.
Convert: 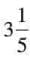 = 16/5.
= 16/5.
Then: 16/5 × 15/4 = (16 × 15)/(5 × 4) = 240/20 = 12.
Alternately: (16 × 15)/(5 × 4) = (4 × 15)/5 = 12.
Reciprocals
- The reciprocal of a fraction x/y is y/x.
- For a whole number x, the reciprocal is 1/x.
- The product of a fraction and its reciprocal is 1.
- Steps to Find:
- Swap the numerator and denominator.
- For mixed fractions, convert to improper fractions first, then swap.
- Example: Find the reciprocal of
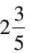 .
.
Convert: 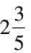 = 13/5.
= 13/5.
Reciprocal: 5/13.
Division of Fractions
- Multiply the first fraction by the reciprocal of the second fraction.
- Steps:
- Convert mixed fractions to improper fractions.
- Find the reciprocal of the divisor (second fraction).
- Multiply the first fraction by this reciprocal.
- Simplify the result.
- Example: Divide
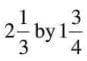 .
.
Convert: 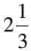 = 7/3,
= 7/3, 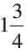 = 7/4.
= 7/4.
The reciprocal of 7/4 is 4/7.
Multiply: 7/3 × 4/7 = (7 × 4)/(3 × 7) = 4/3 = 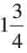 .
.
Operation 'of'
- The word 'of' between fractions means multiplication.
- Solve 'of' operations before other multiplications or divisions in an expression.
- Steps:
- Identify the 'of' operation.
- Multiply the fractions or numbers involved.
- Simplify the result.
- Example: Evaluate 4/5 of 10/11.
- 4/5 × 10/11 = (4 × 10)/(5 × 11) = 40/55 = 8/11.
Combination of Fundamental Operations
- Simplify expressions with multiple operations using BODMAS (Bracket, Of, Division, Multiplication, Addition, Subtraction).
- Steps:
- Solve inside the brackets first.
- Perform the 'of' operations (multiplication).
- Do division and multiplication from left to right.
- Do addition and subtraction from left to right.
- Example: Simplify 4/5 of 10/11 ÷ 9/11 + (2/3 ÷ 3/4).
First, brackets: 2/3 ÷ 3/4 = 2/3 × 4/3 = 8/9.
Then, 'of': 4/5 × 10/11 = 40/55 = 8/11.
Next, division: 8/11 ÷ 9/11 = 8/11 × 11/9 = 8/9.
Finally, add: 8/9 + 8/9 = 16/9 = 1 (7/9).
Word Problems
- Use fractions to solve real-life problems by identifying the whole and the part.
- Steps to Solve:
- Identify the total quantity (whole).
- Determine the fraction representing the part.
- Multiply the fraction by the whole to find the part, or divide to find the whole.
- Simplify and interpret the result.
- Example: Tia read 1/4 of a book on the first day and 2/5 of the remaining book on the second day. If 90 pages are left, find the total pages.
Fraction left after first day: 1 - 1/4 = 3/4.
Second day: 2/5 × 3/4 = 6/20 = 3/10.
Total read: 1/4 + 3/10 = 5/20 + 6/20 = 11/20.
Fraction left: 1 - 11/20 = 9/20.
Since 9/20 of total = 90, total pages = 90 ÷ 9/20 = 90 × 20/9 = 200 pages.
|
44 videos|201 docs|24 tests
|
FAQs on Fractions Chapter Notes - Mathematics Class 6 ICSE
| 1. What is a fraction and how does it represent division? |  |
| 2. What are like and unlike fractions? |  |
| 3. How can a fraction be reduced to its lowest terms? |  |
| 4. How can fractions be represented on a number line? |  |
| 5. What is the process for comparing fractions? |  |
















