Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Chapter Notes: Speed, Distance, and Time
Speed, Distance, and Time Chapter Notes | Mathematics Class 6 ICSE PDF Download
| Table of contents |
|
| Introduction |
|
| Speed |
|
| Units of Speed |
|
| Conversion of Units of Speed |
|
| Solved Examples |
|
Introduction
Imagine you're on a thrilling bike ride, zooming through the streets, or watching a speedy train whiz by! How fast are you going? How far will you travel? How long will it take? These exciting questions are answered by understanding speed, distance, and time. This chapter is like a roadmap to help you figure out how these three ideas work together. Whether it's a car racing down the highway or an athlete sprinting on a track, you'll learn how to calculate their speed, the distance they cover, or the time they take. Get ready to dive into a fun and practical world of motion!
Speed
- Speed is how fast an object moves, measured by the distance it covers in a specific amount of time.
- It tells us how quickly or slowly something travels from one place to another.
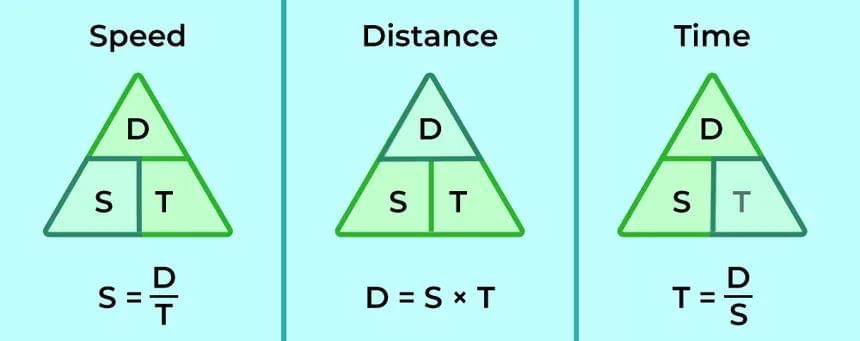
- Formula: Speed = Distance ÷ Time
- From this, we can derive:
- Distance = Speed × Time
- Time = Distance ÷ Speed
- If an object covers the same distance in equal time intervals, its speed is uniform.
- If the distances covered in equal time intervals vary, the speed is variable.
Example: A motorbike travels 120 km in 2 hours.
Step-by-step:
Step-by-step:
- Use the formula: Speed = Distance ÷ Time
- Distance = 120 km, Time = 2 hours
- Speed = 120 km ÷ 2 hours = 60 km/h
- So, the motorbike's speed is 60 km/h.
Units of Speed
- Speed is expressed in units based on distance and time.
- When distance is in kilometres (km) and time is in hours (h), speed is in kilometres per hour (km/h).
- When distance is in meters (m) and time is in seconds (s), speed is in meters per second (m/s).
Example: A car covers 33 km in 30 minutes. Find its speed in km/h.
Step-by-step:
Step-by-step:
- Convert time to hours: 30 minutes = 30 ÷ 60 = 0.5 hours
- Use the formula: Speed = Distance ÷ Time
- Distance = 33 km, Time = 0.5 hours
- Speed = 33 km ÷ 0.5 hours = 33 × 2 = 66 km/h
- So, the car's speed is 66 km/h.
Conversion of Units of Speed
Speed units can be converted to match the required format.
To convert km/h to m/s: Multiply by 5/18.
- Reason: 1 km = 1,000 m, 1 hour = 3,600 s, so 1 km/h = 1,000 m ÷ 3,600 s = 5/18 m/s
To convert km/h to cm/s: Multiply by 250/9.
- Reason: 1 km = 100,000 cm, 1 hour = 3,600 s, so 1 km/h = 100,000 cm ÷ 3,600 s = 250/9 cm/s
To convert m/s to km/h: Multiply by 18/5.
- Reason: 1 m/s = (1 m ÷ 1,000) km ÷ (1 s ÷ 3,600) h = 3,600 ÷ 1,000 = 18/5 km/h
To convert cm/s to km/h: Multiply by 9/250.
- Reason: 1 cm/s = (1 cm ÷ 100,000) km ÷ (1 s ÷ 3,600) h = 3,600 ÷ 100,000 = 9/250 km/h
Example: Convert 90 km/h to m/s.
Step-by-step:
Step-by-step:
- Use the conversion factor: Multiply by 5/18
- Speed = 90 × 5/18 = (90 × 5) ÷ 18 = 450 ÷ 18 = 25 m/s
- So, 90 km/h = 25 m/s.
Solved Examples
Example 1: A train travels at 125 km/h for 3 hours. Find the distance covered.
Step-by-step:
Step-by-step:
- Use the formula: Distance = Speed × Time
- Speed = 125 km/h, Time = 3 hours
- Distance = 125 × 3 = 375 km
- So, the train covers 375 km.
Example 2: A motorbike travels 56 km at a speed of 42 km/h. Find the time taken.
Step-by-step:
Step-by-step:
- Use the formula: Time = Distance ÷ Speed
- Distance = 56 km, Speed = 42 km/h
- Time = 56 ÷ 42 = 4/3 hours = 1 hour 20 minutes
- So, the time taken is 1 hour 20 minutes.
Example 3: Anant runs 250 meters in 50 seconds. Find:
(a) his speed
(b) distance covered in 10 seconds
(c) time taken to cover 1/2 km
Step-by-step:
(a) Speed = Distance ÷ Time = 250 m ÷ 50 s = 5 m/s
(b) Distance = Speed × Time = 5 m/s × 10 s = 50 m
(c) Distance = 1/2 km = 500 m, Time = Distance ÷ Speed = 500 m ÷ 5 m/s = 100 s
So, speed = 5 m/s, distance = 50 m, time = 100 s.
(a) his speed
(b) distance covered in 10 seconds
(c) time taken to cover 1/2 km
Step-by-step:
(a) Speed = Distance ÷ Time = 250 m ÷ 50 s = 5 m/s
(b) Distance = Speed × Time = 5 m/s × 10 s = 50 m
(c) Distance = 1/2 km = 500 m, Time = Distance ÷ Speed = 500 m ÷ 5 m/s = 100 s
So, speed = 5 m/s, distance = 50 m, time = 100 s.
Example 4: A motorist travels 50 km at 40 km/h and 70 km at 60 km/h. Find:
(a) total time taken
(b) average speed
Step-by-step:
(a) total time taken
(b) average speed
Step-by-step:
(a) Time for 50 km = 50 ÷ 40 = 5/4 hours
- Time for 70 km = 70 ÷ 60 = 7/6 hours
- Total time = 5/4 + 7/6 = (15 + 14)/12 = 29/12 hours
(b) Average speed = Total distance ÷ Total time = (50 + 70) ÷ (29/12) = 120 × 12/29 = 49 19/29 km/h
- So, total time = 29/12 hours, average speed = 49 19/29 km/h.
Example 5: Two athletes X and Y run from the same point at 10 km/h and 12 km/h for 3 hours. Find the distance between them if they run:
(a) in the same direction
(b) in opposite directions
Step-by-step:
(a) in the same direction
(b) in opposite directions
Step-by-step:
(a) Distance by X = 10 × 3 = 30 km, Distance by Y = 12 × 3 = 36 km
- Distance between them (same direction) = 36 - 30 = 6 km
(b) Distance between them (opposite directions) = 30 + 36 = 66 km
- So, same direction = 6 km, opposite directions = 66 km.
Example 6: An aeroplane covers 1,500 km in 2.5 hours. Find its speed in:
(a) m/s
(b) km/min
Step-by-step:
(a) m/s
(b) km/min
Step-by-step:
(a) Speed = 1,500 km ÷ 2.5 h = 600 km/h
- Convert to m/s: 600 × 5/18 = 166 2/3 m/s
(b) Speed = 600 km/h ÷ 60 min = 10 km/min
- So, speed = 166 2/3 m/s, 10 km/min.
Example 7: A 200 m long train travels at 90 km/h. Find the time to pass:
(a) a pole
(b) a 325 m long platform
Step-by-step:
(a) a pole
(b) a 325 m long platform
Step-by-step:
Convert speed: 90 km/h = 90 × 5/18 = 25 m/s
(a) Distance = 200 m, Time = 200 ÷ 25 = 8 s
(b) Distance = 200 + 325 = 525 m, Time = 525 ÷ 25 = 21 s
So, the time to pass the pole = 8 s, platform = 21 s.
The document Speed, Distance, and Time Chapter Notes | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|202 docs|24 tests
|
FAQs on Speed, Distance, and Time Chapter Notes - Mathematics Class 6 ICSE
| 1. What is speed and how is it defined in physics? |  |
Ans. Speed is defined as the distance traveled by an object in a given amount of time. In physics, speed is typically measured in units such as meters per second (m/s) or kilometers per hour (km/h). It represents how fast an object is moving regardless of its direction.
| 2. What are the common units of speed used in different contexts? | |
Ans. Common units of speed include meters per second (m/s), kilometers per hour (km/h), and miles per hour (mph). Meters per second is often used in scientific contexts, while kilometers per hour and miles per hour are frequently used in everyday scenarios, such as driving.
| 3. How can we convert speed from one unit to another? | |
Ans. To convert speed from one unit to another, you can use conversion factors. For example, to convert from kilometers per hour (km/h) to meters per second (m/s), you can multiply by 5/18. Conversely, to convert from meters per second to kilometers per hour, you multiply by 18/5. This allows for easy interchangeability between units.
| 4. Can you provide a simple example of calculating speed using distance and time? | |
Ans. Certainly! If a car travels a distance of 150 kilometers in 3 hours, the speed can be calculated using the formula: Speed = Distance ÷ Time. Thus, Speed = 150 km ÷ 3 h = 50 km/h. Therefore, the car's speed is 50 kilometers per hour.
| 5. What is the relationship between speed, distance, and time in a formula? | |
Ans. The relationship between speed, distance, and time is described by the formula: Speed = Distance ÷ Time. This means that if you know any two of these variables, you can easily calculate the third. For example, if you have the speed and time, you can find the distance by rearranging the formula to Distance = Speed × Time.
About this Document
4.71/5
Rating
Oct 02, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Speed, Distance, and Time for Class 6 2025 is part of Mathematics Class 6 ICSE preparation.
The notes and questions for Chapter Notes: Speed, Distance, and Time have been prepared according to the Class 6 exam syllabus. Information about Chapter Notes: Speed, Distance, and Time covers topics
like Introduction, Speed, Units of Speed, Conversion of Units of Speed, Solved Examples and Chapter Notes: Speed, Distance, and Time Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Speed, Distance, and Time.
Introduction of Chapter Notes: Speed, Distance, and Time in English is available as part of our Mathematics Class 6 ICSE
for Class 6 & Chapter Notes: Speed, Distance, and Time in Hindi for Mathematics Class 6 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Speed, Distance, and Time Chapter Notes | Mathematics Class 6 ICSE
Description
Full syllabus notes, lecture & questions for Speed, Distance, and Time Chapter Notes | Mathematics Class 6 ICSE - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 6 ICSE | Best notes, free PDF download
Information about Chapter Notes: Speed, Distance, and Time
In this doc you can find the meaning of Chapter Notes: Speed, Distance, and Time defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Speed, Distance, and Time theory, EduRev gives you an ample number of questions to practice Chapter Notes: Speed, Distance, and Time tests, examples and also practice Class 6
tests
Related Searches
Important questions
,Extra Questions
,mock tests for examination
,Previous Year Questions with Solutions
,MCQs
,and Time Chapter Notes | Mathematics Class 6 ICSE
,Speed
,Sample Paper
,past year papers
,video lectures
,Distance
,Speed
,practice quizzes
,Objective type Questions
,study material
,Free
,ppt
,Exam
,Viva Questions
,Summary
,shortcuts and tricks
,and Time Chapter Notes | Mathematics Class 6 ICSE
,Distance
,and Time Chapter Notes | Mathematics Class 6 ICSE
,Speed
,Distance
,Semester Notes
;
Additional Information about Chapter Notes: Speed, Distance, and Time for Class 6 Preparation
Chapter Notes: Speed, Distance, and Time Free PDF Download
The Chapter Notes: Speed, Distance, and Time is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Speed, Distance, and Time now and kickstart your journey towards success in the Class 6 exam.
Importance of Chapter Notes: Speed, Distance, and Time
The importance of Chapter Notes: Speed, Distance, and Time cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Speed, Distance, and Time
Chapter Notes: Speed, Distance, and Time Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Speed, Distance, and Time.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Speed, Distance, and Time Notes on EduRev are your ultimate resource for success.
Chapter Notes: Speed, Distance, and Time Class 6 Questions
The "Chapter Notes: Speed, Distance, and Time Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Speed, Distance, and Time on the App
Students of Class 6 can study Chapter Notes: Speed, Distance, and Time alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Speed, Distance, and Time,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Speed, Distance, and Time is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily