Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Chapter Notes: Angles
Angles Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Angles are all around us, shaping the way we see and understand the world! From the sharp corner of a book to the wide sweep of a clock's hands, angles help us measure and describe directions and rotations. This chapter takes you on an exciting journey to explore angles, their types, how they’re named, and how we measure or even create them using simple tools. Get ready to dive into the fascinating world of angles, where lines meet to form shapes and patterns that spark curiosity!
Angle
- An angle is formed when two rays share the same starting point.
- The rays are called the arms or sides of the angle.
- The common starting point is called the vertex.
Example: Rays OA and OB start at point O. They form an angle with O as the vertex and OA, OB as the arms.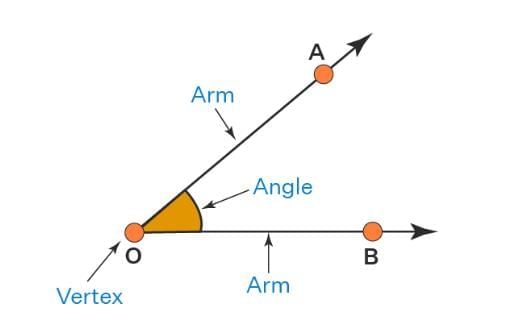
Naming of an Angle
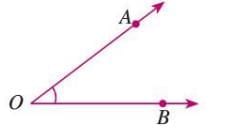
- An angle is denoted by the symbol ∠.
- It can be named using three letters, with the middle letter as the vertex (e.g., ∠AOB or ∠BOA).
- It can also be named using just the vertex (e.g., ∠O).
- Angles can be labeled with numbers (e.g., ∠1, ∠2) or small letters (e.g., ∠a, ∠b).
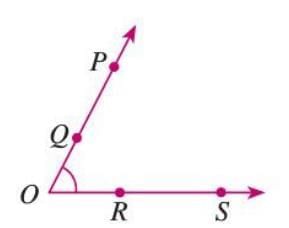
Example: In a figure, ∠O can also be written as ∠POS, ∠POR, ∠QOR, or ∠QOS, depending on the points on the rays.
Points to Remember:
- In a three-letter name like ∠ABC, the middle letter (B) is always the vertex.
- An angle can have multiple names based on points along its arms.
Interior and Exterior of an Angle
- The area between the two arms of an angle is called its interior.
- The area outside the arms is called the exterior.
- The arms themselves form the boundary of the angle.
- Any point in a plane is either inside, outside, or on the boundary of the angle.
Example: In ∠AOB, the shaded region between arms OA and OB is the interior, the white region outside is the exterior, point P is inside, point Q is outside, and points A, R, O, B, S are on the boundary.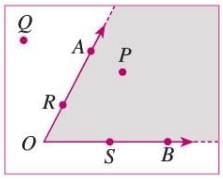
Points to Remember:
- The interior and exterior extend endlessly as the rays go on infinitely.
- The arms separate the interior from the exterior.
Magnitude of an Angle
- The size of an angle is its magnitude, measured by how much one arm rotates around the vertex to meet the other arm.
- The unit of measurement is degrees, denoted by °.
Example: In ∠PQR, the magnitude is the rotation needed for arm QR to align with arm QP.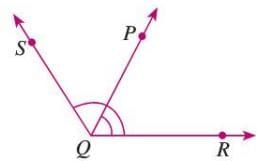
Types of Angles
Angles are classified based on their magnitude.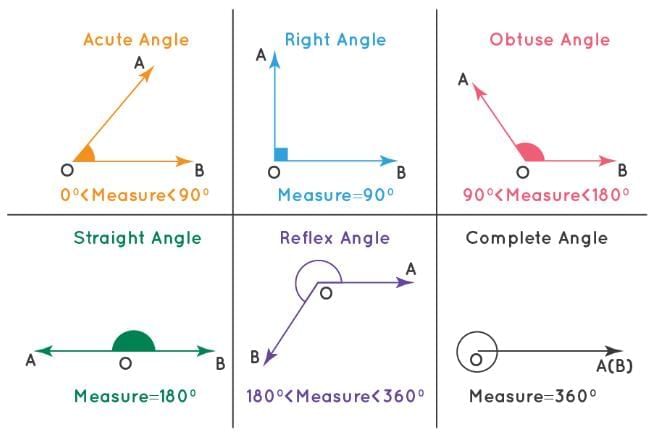
Acute Angle
- An angle measuring more than 0° but less than 90°.
Example: Angles like 15°, 30°, or 45° are acute angles.
Right Angle
- An angle measuring exactly 90°.
Example: An angle of 90° is a right angle, like the corner of a square.
Obtuse Angle
- An angle measuring more than 90° but less than 180°.
Example: Angles like 96°, 118°, or 175° are obtuse angles.
Straight Angle
- An angle measuring exactly 180°.
Example: An angle of 180° forms a straight line.
Reflex Angle
- An angle measuring more than 180° but less than 360°.
Example: Angles like 188°, 220°, or 350° are reflex angles.
Points to Remember:
- Lines, rays, or segments forming a right angle are perpendicular.
- The sum of angles around a point is always 360°.
- Formula: ∠AOB + ∠BOC + ∠COD + ∠DOA = 360°.
Some Special Angles
Zero Angle
- An angle where the ray doesn’t rotate, so the magnitude is 0°.
Example: If a ray’s initial and final positions are the same without rotation, it forms a 0° angle.
Complete Angle
- An angle formed by one full rotation of a ray, measuring 360°.
Example: If ray OA rotates fully and returns to its starting position, it forms a 360° complete angle.
Special Pairs of Angles
Congruent Angles
- Angles with the same magnitude are congruent.
Example: If ∠ABC = 30° and ∠MNO = 30°, they are congruent angles.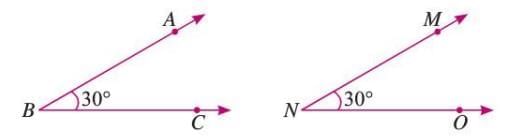
Vertically Opposite Angles
- Angles formed by two intersecting lines with no common arm.
- They are always equal.
Example: If two lines intersect, ∠m = ∠n and ∠x = ∠y are vertically opposite angles.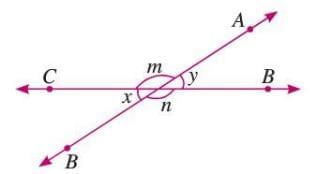
Complementary Angles
- Two angles whose measures add up to 90°.
- Formula: ∠A + ∠B = 90°.
Example: If ∠ABC = 60° and ∠PQR = 30°, then 60° + 30° = 90°, so they are complementary.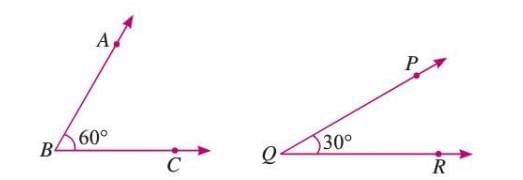
Supplementary Angles
- Two angles whose measures add up to 180°.
- Formula: ∠A + ∠B = 180°.
Example: If ∠ABC = 120° and ∠PQR = 60°, then 120° + 60° = 180°, so they are supplementary.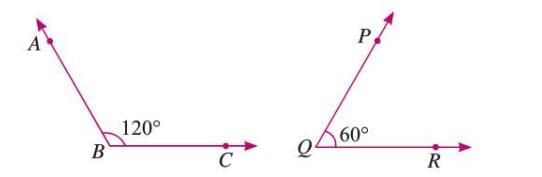
Adjacent Angles
- Two angles sharing a common arm and vertex, lying on opposite sides of the common arm.
Example: ∠AOB and ∠BOC are adjacent angles with OB as the common arm and O as the vertex.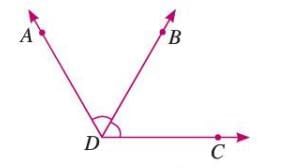
Linear Pair
- Two adjacent angles that are supplementary (sum to 180°).
- Formula: ∠A + ∠B = 180° (where ∠A and ∠B are adjacent).
Example: ∠AOC and ∠BOC are adjacent and sum to 180°, forming a linear pair.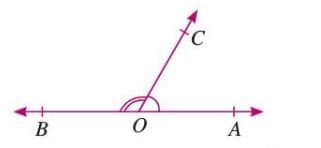
Measurement of a Line Segment
- A line segment’s length can be measured using two methods:
By Ruler
- Place the ruler’s 0 mark at one end of the segment.
- Align the ruler along the segment.
- Read the mark where the other end of the segment falls.
- Units are usually centimeters (cm) or millimeters (mm).
Example: For line segment AB, align the ruler with 0 at A, and read the mark at B. If it’s 4 cm, then AB = 4 cm.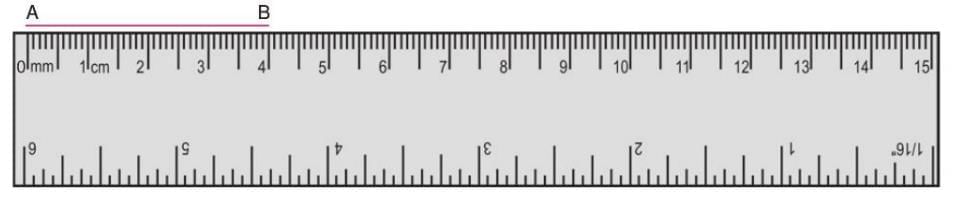
By Divider and Ruler
- Place one end of the divider at point A and adjust it to reach point B.
- Keep the divider’s opening fixed and place it on the ruler with one end at 0.
- Read the ruler mark where the other end of the divider falls.
Example: For line segment AB, set the divider from A to B, then place it on a ruler. If the ruler shows 4 cm, then AB = 4 cm.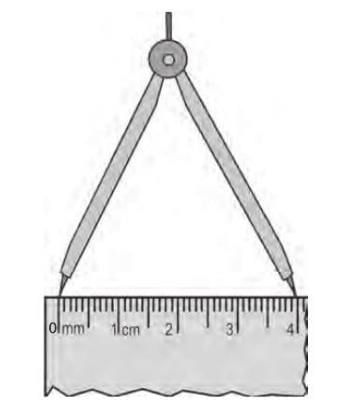
Why Divider is Better: Using a divider and ruler reduces errors from angular viewing, unlike using a ruler alone.
Measurement of an Angle
- Angles are measured in degrees (°).
- One complete rotation around a point is 360°.
- 1° is divided into 60 minutes (′), and 1 minute is divided into 60 seconds (″).
Formulas:
- 1 complete rotation = 360°
- 1° = 60′
- 1′ = 60″
Example: Find the angle that is 10°15′30″ smaller than 120°10′50″.
Solution:
- Subtract: 120°10′50″ − 10°15′30″
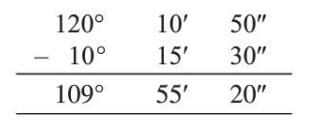
- Degrees: 120° − 10° = 110°
- Minutes: 10′ − 15′ = −5′ (borrow 1° = 60′)
- Degrees become: 110° − 1° = 109°, Minutes: 60′ + 10′ − 15′ = 55′
- Seconds: 50″ − 30″ = 20″
- Result: 109°55′20″
Use of Protractor to Measure an Angle
- A protractor is a tool for measuring and constructing angles.
- It has a circular scale marked from 0° to 180°.
- Inner scale measures angles in the anticlockwise direction.
- Outer scale measures angles in the clockwise direction.
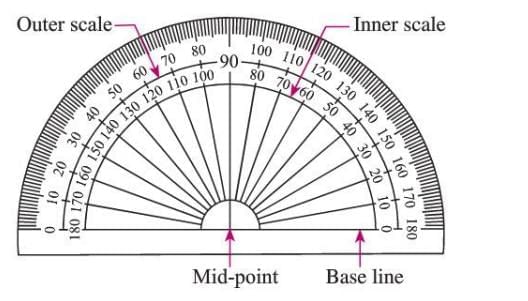
Steps to Measure:
- Place the protractor’s midpoint on the angle’s vertex.
- Align the base line with one arm (ray).
- Read the degree mark where the other arm falls on the appropriate scale.
- Use the inner scale for angles opening to the right, outer scale for angles opening to the left.
Example: To measure ∠AOB, place the protractor’s midpoint on O.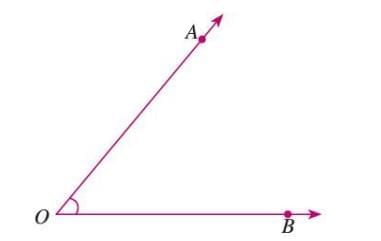
Align the base with ray OB, and read the inner scale where ray OA falls. If it’s 50°, then ∠AOB = 50°.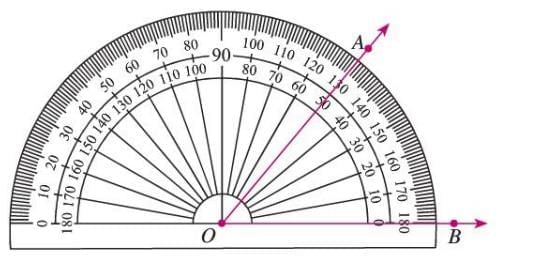
Solved Example: Measure ∠PQR, where the arc is on the outer side (reflex angle).
Solution:
- Place the protractor’s midpoint on Q, base on ray QR.
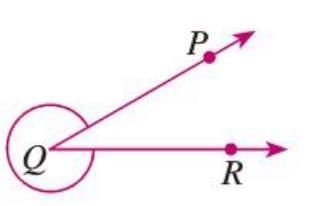
- Use the outer scale (since the arc is outer) to measure ∠PQR = 30°.
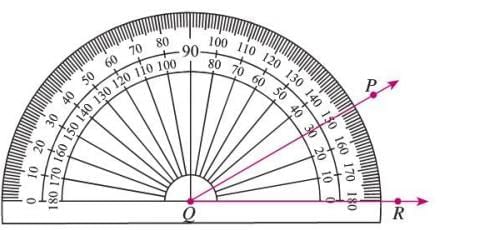
- For reflex angle: 360° − 30° = 330°.
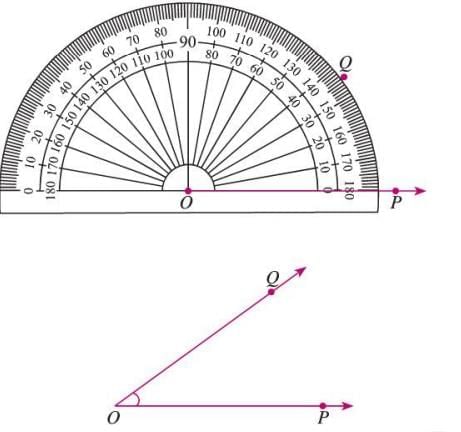
Use of Protractor to Construct an Angle
Steps to Construct:
- Draw a ray (e.g., OP) with starting point O.
- Place the protractor’s midpoint on O, align the base with ray OP.
- Use the inner scale (for angles opening right) and mark the desired degree (e.g., 36°).
- Remove the protractor and draw a ray from O to the marked point (Q).
- The angle formed (e.g., ∠POQ) is the required angle.
- For reflex angles (>180°), construct the smaller angle (360° − desired angle) and mark the outer arc.
The document Angles Chapter Notes | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|201 docs|24 tests
|
FAQs on Angles Chapter Notes - Mathematics Class 6 ICSE
| 1. What is an angle and how is it formed? |  |
Ans. An angle is formed when two rays originate from the same endpoint, known as the vertex. The rays are called the sides of the angle. Angles are measured in degrees, and they can represent the amount of rotation from one ray to the other.
| 2. How do you name an angle? | |
Ans. Angles are typically named using three points: one point on each ray and the vertex point in the middle. For example, if the rays are named A and B, and the vertex is point C, the angle can be named as ∠ABC or ∠C.
| 3. What are the different types of angles? | |
Ans. There are several types of angles based on their measurements: acute angles (less than 90 degrees), right angles (exactly 90 degrees), obtuse angles (greater than 90 degrees but less than 180 degrees), straight angles (exactly 180 degrees), reflex angles (greater than 180 degrees but less than 360 degrees), and full angles (exactly 360 degrees).
| 4. What is the difference between interior and exterior angles? | |
Ans. Interior angles are the angles formed inside a shape or between the sides of an angle. In contrast, exterior angles are formed outside of a shape or angle. For example, when two lines intersect, the angles on the inside are the interior angles, while the angles formed on the outside are the exterior angles.
| 5. How do you measure an angle? | |
Ans. Angles are measured using a protractor. To measure an angle, you place the protractor's center point on the vertex of the angle, align one side of the angle with the baseline of the protractor, and then read the degree measurement where the other side intersects the scale.
About this Document
4.72/5
Rating
Oct 02, 2025
Last updated
Document Description: Chapter Notes: Angles for Class 6 2025 is part of Mathematics Class 6 ICSE preparation.
The notes and questions for Chapter Notes: Angles have been prepared according to the Class 6 exam syllabus. Information about Chapter Notes: Angles covers topics
like Introduction, Angle, Naming of an Angle, Interior and Exterior of an Angle, Magnitude of an Angle, Types of Angles, Some Special Angles, Special Pairs of Angles, Measurement of a Line Segment, Measurement of an Angle, Use of Protractor to Measure an Angle, Use of Protractor to Construct an Angle and Chapter Notes: Angles Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Angles.
Introduction of Chapter Notes: Angles in English is available as part of our Mathematics Class 6 ICSE
for Class 6 & Chapter Notes: Angles in Hindi for Mathematics Class 6 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Angles Chapter Notes | Mathematics Class 6 ICSE
Description
Full syllabus notes, lecture & questions for Angles Chapter Notes | Mathematics Class 6 ICSE - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 6 ICSE | Best notes, free PDF download
Information about Chapter Notes: Angles
In this doc you can find the meaning of Chapter Notes: Angles defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Angles theory, EduRev gives you an ample number of questions to practice Chapter Notes: Angles tests, examples and also practice Class 6
tests
Related Searches
Summary
,Semester Notes
,ppt
,Angles Chapter Notes | Mathematics Class 6 ICSE
,Extra Questions
,mock tests for examination
,Sample Paper
,video lectures
,Angles Chapter Notes | Mathematics Class 6 ICSE
,Free
,Viva Questions
,Exam
,Important questions
,Objective type Questions
,MCQs
,shortcuts and tricks
,practice quizzes
,study material
,Angles Chapter Notes | Mathematics Class 6 ICSE
,past year papers
,Previous Year Questions with Solutions
;
Additional Information about Chapter Notes: Angles for Class 6 Preparation
Chapter Notes: Angles Free PDF Download
The Chapter Notes: Angles is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Angles now and kickstart your journey towards success in the Class 6 exam.
Importance of Chapter Notes: Angles
The importance of Chapter Notes: Angles cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Angles
Chapter Notes: Angles Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Angles.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Angles Notes on EduRev are your ultimate resource for success.
Chapter Notes: Angles Class 6 Questions
The "Chapter Notes: Angles Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Angles on the App
Students of Class 6 can study Chapter Notes: Angles alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Angles,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Angles is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup