Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Chapter Notes: Numbers
Numbers Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Numbers are the heart of mathematics, acting like magic keys that unlock the ability to count, measure, compare, and organise the world around us! From tallying the number of friends in a classroom to checking the weight of your favourite snacks, numbers make everyday tasks fun and meaningful. They help us label things like vehicle number plates or estimate crowds at events, making life more orderly and exciting. Let’s dive into the fascinating world of numbers and explore how they work in the Hindu-Arabic system, their values, and how we use them in various ways!

Numeral
- Definition: A numeral is a symbol or group of symbols used to represent a number.
- In the Hindu-Arabic system, numerals are formed using digits like 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- Examples include single-digit numerals, such as 5, or multi-digit numerals, like 123 or 4,567.
- Example: The numeral 735 represents the number seven hundred thirty-five using the digits 7, 3, and 5.
Hindu-Arabic System of Numeration
- Definition: This is a decimal system using ten digits (0 to 9) to form numerals, based on place value.
- Origin: Developed by Hindu mathematicians, enhanced by Arabs, and later introduced to Europe.
- Key Feature: Uses base-10, where each position represents a power of 10.
- Steps of the system:
- Ten 'ones' = 1 ten (10 × 1 = 10).
- Ten 'tens '= 1 hundred (10 × 10 = 100).
- Ten 'hundreds' = 1 thousand (10 × 100 = 1,000).
- Also called the denary or base-10 system.
- Example: In the Hindu-Arabic system, the numeral 123 is formed using digits 1, 2, and 3, where 1 is in the hundreds place, 2 in the tens place, and 3 in the ones place.
Face Value
- Definition: The face value of a digit is the value of the digit itself, regardless of its position in the numeral.
- Also known as the true value.
- Key Point: Face value remains constant no matter where the digit appears.
- Example: In the numerals 900 and 56,097, the face value of the digit 9 is always 9.
Place Value
- Definition: The place value of a digit is found by multiplying its face value by the value of its position in the numeral.
- Also called the local value.
- Steps to find place value:
- Identify the digit’s position (e.g., ones, tens, hundreds).
- Multiply the digit’s face value by the place’s value (e.g., 1, 10, 100).
- Formula: Place value = Face value × Value of the place.
- Example: In the numeral 986:
- Digit 6 is in the ones place, so place value = 6 × 1 = 6.
- Digit 8 is in the tens place, so place value = 8 × 10 = 80.
- Digit 9 is in the hundreds place, so place value = 9 × 100 = 900.
Example: Find the place value of the two 7s in 7,12,657 and their sum.
- First 7 (ones place): Place value = 7 × 1 = 7.
- Second 7 (lakhs place): Place value = 7 × 1,00,000 = 7,00,000.
- Sum = 7 + 7,00,000 = 7,00,007.
Points to Remember
- Face value of a digit is always the same, regardless of its position.
- Place value changes based on the digit’s position in the numeral.
- The digit 0 has the same face value and place value (0) in any position.
- For a digit in the ones place, face value equals place value.
Indian Place Value Chart
- A system used in India to organise large numbers with commas separating thousands, lakhs, crores, etc.
- Structure: Commas are placed after the first three digits from the right, then after every two digits.
- Place values:

- Example: For the number 75698027: Insert commas: 7,56,98,027.
- Number name: Seven crore fifty-six lakh ninety-eight thousand twenty-seven.
International Place Value Chart
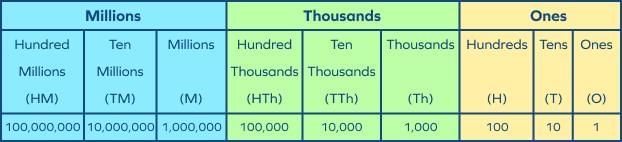
- Definition: A system used globally where commas separate thousands, millions, billions, etc.
- Structure: Commas are placed after every three digits from the right.
- Example: For the number 75698027:
- Insert commas: 75,698,027.
- Number name: Seventy-five million six hundred ninety-eight thousand twenty-seven.
Expanded Form of a Number
- Definition: Writing a number as the sum of the place values of its digits.
- Steps:
- Identify each digit and its place value.
- Multiply each digit by its place value.
- Write the number as the sum of these products.
- Example: For the number 95,021:
- Expanded form: 9 × 10,000 + 5 × 1,000 + 0 × 100 + 2 × 10 + 1 × 1.
Comparison of Numbers
- Definition: Determining which of two numbers is larger.
- Rules:
- Rule 1: A number with more digits is always larger.
- Rule 2: If numbers have the same number of digits, compare digits from the leftmost side. The number with the larger digit in the first differing position is larger.
- Example: Arrange 31,22,567, 34,21,657, 3,43,56,210, 3,44,59,610, 4,44,02,057in descending order.
- Step 1: Identify digits:
- 31,22,567 and 34,21,657 (7 digits).
- 3,43,56,210 and 3,44,59,610 (8 digits).
- 4,44,02,057 (8 digits).
- Step 2: Compare 8-digit numbers:
- 4,44,02,057 (starts with 4) is larger than 3,43,56,210 and 3,44,59,610 (start with 3).
- Compare 3,43,56,210 and 3,44,59,610: At the ten lakhs place, 4 > 3, so 3,44,59,610 > 3,43,56,210.
- Step 3: Compare 7-digit numbers:
- 31,22,567 vs. 34,21,657: At the ten lakhs place, 3 = 3, but at the lakhs place, 1 < 4, so 34,21,657 > 31,22,567.
- Result: 4,44,02,057 > 3,44,59,610 > 3,43,56,210 > 34,21,657 > 31,22,567.
Forming Numbers
- Definition: Creating numbers by arranging given digits, with or without repetition, and in a specific order if required.
- Types:
- With repetition: Digits can be used multiple times.
- Without repetition: Each digit is used only once.
- Example: Using digits 3 and 7 at least once, form all possible 3-digit numberswith repetition:
- Possible numbers: 337, 373, 377, 733, 737, 773.
Forming the Smallest and the Greatest Number
- Smallest Number:
- Place the smallest non-zero digit in the leftmost position.
- Arrange remaining digits in ascending order.
- Note: Zero cannot be the leftmost digit for multi-digit numbers.
- Greatest Number:
- Place the largest digit in the leftmost position.
- Arrange remaining digits in descending order.
- Example: Form the smallest and greatest 6-digit numbers using digits 8, 9, 1, 0, 4, 6without repetition:
- Smallest: Start with 1 (smallest non-zero), then 0, 4, 6, 8, 9 in ascending order: 1,04,689.
- Greatest: Start with 9, then 8, 6, 4, 1, 0 in descending order: 9,86,410.
- Solved Example: Form the smallest and greatest 6-digit numbers:
- Smallest: Start with 1, followed by five 0s: 1,00,000.
- Greatest: Use 9 in all six places: 9,99,999.
Operations on Large Numbers
- Definition: Performing addition, subtraction, multiplication, and division on large numbers.
- Example: A bookstore sold books worth ₹3,85,891 in the first week and ₹4,00,768 in the second week. Find the total sale and which week had greater sales.
- Total sale = 3,85,891 + 4,00,768 = 7,86,659.
- Compare: 4,00,768 > 3,85,891 (leftmost digit 4 > 3).
- Difference = 4,00,768 - 3,85,891 = 14,877.
- Result: Total sale is ₹7,86,659; second week had greater sales by ₹14,877.
- Solved Example: A machine manufactures 3,215 screws daily. How many screws in January (31 days)?
- Screws = 3,215 × 31 = 99,665.
- Solved Example: To stitch a shirt, 2 m 15 cm (215 cm) cloth is needed. From 40 m (4,000 cm), how many shirts can be stitched, and how much cloth remains?
- Number of shirts = 4,000 ÷ 215 = 18 (quotient).
- Remainder = 130 cm (1 m 30 cm).
- Result: 18 shirts, 1 m 30 cm cloth remains.
Estimation
- Definition: Approximating a number to make calculations easier, often to the nearest tens, hundreds, or thousands.
- Also called rounding off.
- Purpose: Provides a general idea when exact numbers are not needed.
Estimation or Rounding Off the Numbers to the Nearest Tens
- Steps:
- Check the digit in the ones place.
- If 0–4, replace it with 0, keep other digits unchanged.
- If 5–9, replace it with 0 and add 1 to the tens place digit.
- Example: Estimate 46,785to the nearest tens:
- Ones place digit = 5.
- Since 5 ≥ 5, replace 5 with 0 and add 1 to tens place (8 + 1 = 9).
- Result: 46,790.
Estimation or Rounding Off the Numbers to the Nearest Hundreds
- Steps:
- Check the digit in the tens place.
- If 0–4, replace tens and ones digits with 0, keep other digits unchanged.
- If 5–9, replace tens and ones digits with 0 and add 1 to the hundreds place digit.
- Example: Estimate 46,785to the nearest hundreds:
- Tens place digit = 8.
- Since 8 > 5, replace tens and ones digits with 0, add 1 to hundreds place (7 + 1 = 8).
- Result: 46,800.
Estimation or Rounding Off the Numbers to the Nearest Thousands
- Steps:
- Check the digit in the hundreds place.
- If 0–4, replace hundreds, tens, and ones digits with 0, keep other digits unchanged.
- If 5–9, replace hundreds, tens, and ones digits with 0 and add 1 to the thousands place digit.
- Example: Estimate 3,621to the nearest thousands:
- Hundreds place digit = 6.
- Since 6 > 5, replace hundreds, tens, and ones digits with 0, add 1 to thousands place (3 + 1 = 4).
- Result: 4,000.
Estimation in Sum or Difference
- Definition: Rounding numbers before adding or subtracting to get an approximate result.
- Choose the place (tens, hundreds, thousands) based on required accuracy.
- Example: Estimate 730 + 998to the nearest hundreds:
- 730 rounds to 700.
- 998 rounds to 1,000.
- Estimated sum = 700 + 1,000 = 1,700.
- Solved Example: Estimate 439 + 334 + 4,317to the nearest hundreds and tens:
- Nearest hundreds:
- 439 → 400, 334 → 300, 4,317 → 4,300.
- Sum = 400 + 300 + 4,300 = 5,000.
- Nearest tens:
- 439 → 440, 334 → 330, 4,317 → 4,320.
- Sum = 440 + 330 + 4,320 = 5,090.
Estimation in Product or Quotient
- Definition: Rounding numbers before multiplying or dividing to get an approximate result.
- General Rule: Round each number to its greatest place value for quick and reasonable estimates.
- Example: Estimate 9,250 × 29:
- 9,250 rounds to 9,000 (nearest thousands).
- 29 rounds to 30 (nearest tens).
- Estimated product = 9,000 × 30 = 2,70,000.
- Solved Example: Estimate 477 ÷ 19:
- 477 rounds to 500 (nearest hundreds).
- 19 rounds to 20 (nearest tens).
- Estimated quotient = 500 ÷ 20 = 25.
The document Numbers Chapter Notes | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|201 docs|24 tests
|
FAQs on Numbers Chapter Notes - Mathematics Class 6 ICSE
| 1. What is the Hindu-Arabic system of numeration? |  |
Ans. The Hindu-Arabic system of numeration is the most widely used numeral system in the world. It consists of ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This system is positional, meaning the value of a digit depends on its position within a number. For example, in the number 345, the digit 3 represents 300, the digit 4 represents 40, and the digit 5 represents 5.
| 2. What is the difference between face value and place value? |  |
Ans. Face value refers to the value of a digit itself, regardless of its position in the number. For example, in the number 678, the face value of 7 is 7. Place value, on the other hand, is the value of a digit based on its position in the number. In the same example, the place value of 7 is 70, as it is in the tens place.
| 3. How do the Indian and International place value charts differ? |  |
Ans. The Indian place value chart groups numbers in lakhs and crores, while the International place value chart uses thousands and millions. In the Indian system, the first three digits from the right are grouped as ones, tens, and hundreds, followed by lakhs (100,000) and crores (10,000,000). In the International system, the first three digits are grouped as ones, tens, and hundreds, followed by thousands (1,000) and millions (1,000,000).
| 4. What is the expanded form of a number? |  |
Ans. The expanded form of a number expresses it as the sum of the values of its digits based on their place value. For example, the expanded form of 456 is 400 + 50 + 6. This helps to understand the contribution of each digit to the overall value of the number.
| 5. How can numbers be compared effectively? |  |
Ans. Numbers can be compared by looking at their digits from left to right, starting with the highest place value. The number with the larger digit in the highest place value is greater. If the digits are the same, we move to the next place value until a difference is found. For example, to compare 482 and 479, we see that both have 4 in the hundreds place, then 8 in the tens place (greater in 482), making 482 the larger number.
Related Searches
















