Symmetry Chapter Notes | Mathematics Class 6 ICSE PDF Download
Introduction
Imagine folding a piece of paper in half and finding that both sides match perfectly, like a butterfly's wings or a heart shape. This fascinating concept is called symmetry, and it’s all around us in nature, art, and even the letters we write! In this chapter, we’ll explore how shapes can be divided into identical halves, learn about lines that act like mirrors, and discover how to create symmetric figures. Symmetry is like a magical balance in shapes that makes them visually appealing and mathematically interesting. Let’s dive into the world of symmetry and uncover its secrets step by step!
Symmetry
- Symmetry refers to shapes or objects where one half is a mirror image of the other half.
- These shapes are called symmetric figures, and their halves are identical in size and shape.
- Shapes that do not have identical halves are called nonsymmetric figures.
- A figure is symmetric if it can be folded along a line, and both halves overlap perfectly.
- Example: A heart shape is symmetric because folding it vertically through its centre makes both halves match exactly.
Line of Symmetry
- A line of symmetry is a line that divides a figure into two mirror-image halves.
- When folded along this line, the two halves of the figure overlap completely.
- This line is also called the axis of symmetry.
- Different shapes have different numbers of lines of symmetry based on their structure.
- Example: A square has four lines of symmetry—two along the midpoints of opposite sides and two along its diagonals.
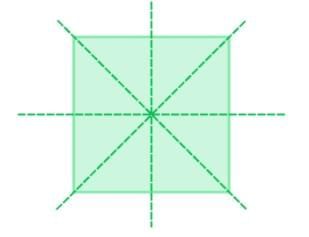
Number of Lines of Symmetry for Common Shapes: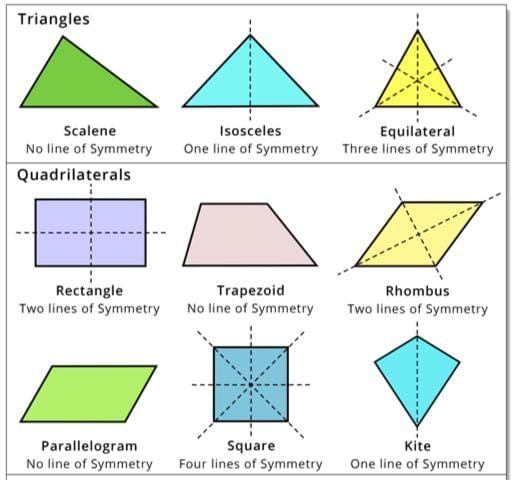
- Isosceles triangle: 1 line of symmetry (angle bisector of the vertex angle).
- Equilateral triangle: 3 lines of symmetry (angle bisectors, which are also perpendicular bisectors of the sides).
- Rectangle: 2 lines of symmetry (perpendicular bisectors of opposite sides).
- Square: 4 lines of symmetry (perpendicular bisectors of sides and diagonals).
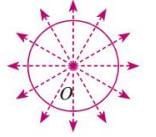
- Circle: Infinite lines of symmetry (any line passing through the center).
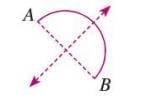
- Arc: 1 line of symmetry (perpendicular bisector of the line joining its endpoints).
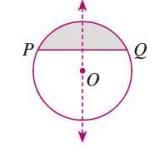
- Segment: 1 line of symmetry (perpendicular bisector of the chord).
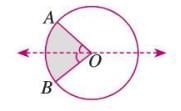
- Sector: 1 line of symmetry (angle bisector of the radii forming the sector).
- Arrowhead: 1 line of symmetry (along the central axis).
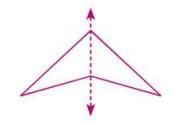
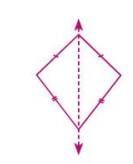
- Kite-shaped figure: 1 line of symmetry (along the diagonal connecting the vertices of unequal angles).
- Scalene triangle: 0 lines of symmetry (no equal sides or angles).
Reflection and Symmetry
- Reflection symmetry occurs when an object and its mirror image are symmetric with respect to a line (the mirror line).
- The mirror line acts as the line of symmetry, and the reflected image is a mirror image of the original.
- The reflected image is congruent to the original, meaning all lengths and angles remain the same.
- However, the image is laterally inverted, meaning left and right are swapped.
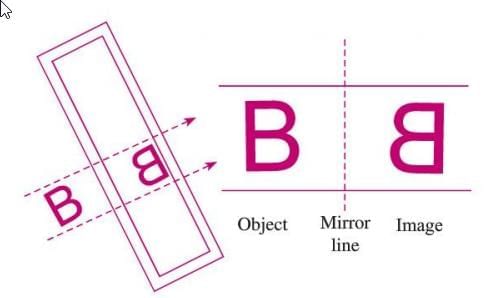
- Steps to Understand Reflection Symmetry:
- Place an object in front of a mirror.
- Observe the mirror image, which is symmetric to the object with respect to the mirror line.
- Fold a paper along the mirror line to see the object and its image overlap.
To Construct a Point Symmetric to a Given Point with Respect to a Line
This construction finds a point C that is symmetric to a given point A with respect to a line PQ.
Steps for Construction:
- Step 1: From point A, draw a line AB perpendicular to line PQ.
- Step 2: Extend line AB beyond point B.
- Step 3: With point B as the center and radius AB, draw an arc to intersect the extended line at point C.
- Step 4: Point C is symmetric to point A with respect to line PQ.
Example: Given a point A and a line PQ, construct point C such that C is the reflection of A over PQ.
- Draw line AB perpendicular to PQ from point A, intersecting PQ at B.
- Extend AB and measure distance AB.
- Draw an arc with center B and radius AB to find point C.
- Point C is symmetric to A because PQ is the perpendicular bisector of segment AC.
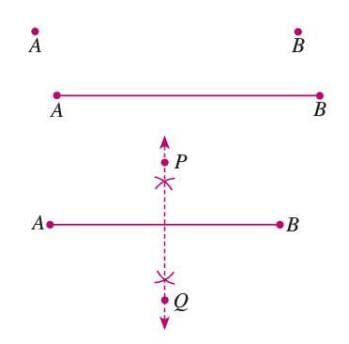
To Construct a Line with Respect to Which Two Given Points are Symmetric
This construction finds a line PQ such that two given points A and B are symmetric with respect to it.
Steps for Construction:
- Step 1: Draw a line segment joining points A and B.
- Step 2: Construct the perpendicular bisector PQ of segment AB.
- Step 3: Line PQ is the line of symmetry, as points A and B are reflections of each other over PQ.
Solved Example: Construct the line of symmetry for letters ' K' and 'Y'.
For letter 'K'. It has one horizontal line of symmetry.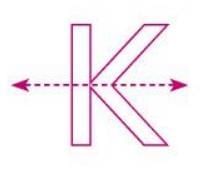
For letter 'Y'. It has a single line of vertical symmetry.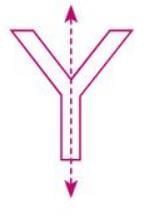
|
44 videos|202 docs|24 tests
|
FAQs on Symmetry Chapter Notes - Mathematics Class 6 ICSE
| 1. What is symmetry, and why is it important in mathematics? |  |
| 2. How do you define reflection symmetry? |  |
| 3. Can you explain how to construct a point symmetric to a given point with respect to a line? |  |
| 4. What steps are involved in constructing a line with respect to which two given points are symmetric? |  |
| 5. How can symmetry be observed in everyday life? |  |















