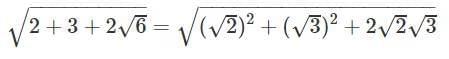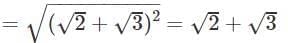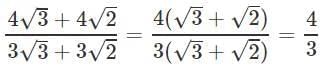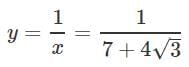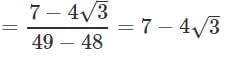Important Questions: Number System | Mathematics (Maths) Class 9 PDF Download

Q1: $\mathrm{Show}\mathrm{ that }0.3333\dots =0.3¯\mathrm{can}\mathrm{ be}\mathrm{ expressed}\mathrm{ in}\mathrm{ the }\mathrm{form}p/q,\mathrm{where}\mathrm{ p}\mathrm{ and}\mathrm{ q }\mathrm{are}\mathrm{ integers}\mathrm{ and}\mathrm{ q}\ne 0.$

Sol:

Let x = 0.3333…. 

Multiply with 10,

10x = 3.3333…

Now, 3.3333… = 3 + x (as we assumed x = 0.3333…)

Thus, 10x = 3 + x

10x – x = 3

9x = 3

x = 1/3

Therefore, 0.3333… = 1/3. Here, 1/3 is in the form of p/q and q ≠ 0.

Q2. If 'a' and 'b' are rational numbers and:

3 + √83 − √8 = a + b√8

Find the value of 'a' and 'b':

Solution:
Rationalizing the fraction, we get:

3 + √83 − √8 = (3 + √8) × (3 + √8)(3 − √8) × (3 + √8)

= (3 + √8)²3² − (√8)²

= 9 + 8 + 6√89 − 8 = 17 + 6√81

= 17 + 6√8

Now:

3 + √83 − √8 = a + b√8

Equating a and b both sides
⇒ a + b√8 = 17 +6√8
⇒ a = 17and b = 6

Q3.Simplify the following expressions:

​(√3 – √3)²

Solution: (√3 – √3)² 
= 3 + 3 − 2×√3×√3
= 6 − 6
= 0

Q4. Find two rational numbers between 0.1 and 0.3.

Sol:  Express $0.1$ and $0.3$ as rational numbers with the same denominator:

$0.1=\frac{1}{10}, 0.3=\frac{3}{10}$

Now, the rational numbers between $\frac{1}{10}$ and $\frac{3}{10}$ can be written with a larger denominator to find numbers in between.
Let us express them with a denominator of $100$100:

$0.1=\frac{10}{\mathrm{100 }},0.3=\frac{30}{\mathrm{100 }}\mathrm{ .}$

The rational numbers between $\frac{10}{100}$ and $\frac{30}{100}$ are:

$\frac{11}{100},\frac{12}{100},\frac{13}{100},\dots ,\frac{29}{100}.$

any two:

$\frac{12}{100},\frac{25}{100}.$$<br>$

Q5. Find (64)-1/3

As, 64 = 4 x 4 x 4 = 4³

∴ (64)-1/3 = 1(64)1/3 = 1(43)1/3
= 14^3×1/3 = 14
Thus, (64)-1/3 = 14

Q6. Find a rational number lying between 15  and  12

Rational numbers between   12 and  15 are infinite. Some of them are  310 ,   410 ,   45100 ,  35100  .Step-by-step explanation:As per the question, We need to find rational numbers lying between   15  and  12  As we know,

• Rational Numbers are numbers that can be expressed in the form of p/q where q is not equal to zero.
• Now, we know that  15 = 0.2 and 12  = 0.5
• So, numbers between 0.2 and 0.5 are infinite. Some of them are 0.3,0.4,0.45,,0.35 etc.
• And these may be written as  310 ,   410 ,   45100 ,  35100  etc.

Hence, Rational numbers between 15  and  12 are infinite. Some of them are 310 ,   410 ,   45100 ,  35100

Q7. Find the value of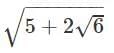 

Ans.

Q8. find the value of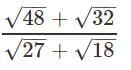  

Ans. 

​Q9. if x = 2 and y = 4, what is value of (x/y)^x-y + (y/x)^y-x

Ans. (2/4)^-2 + (4/2)^4-2 = 2² + 2² = 8

Q10. If xy = 1 and x = 7 + 4√3, what is the value of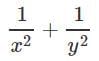  

Ans. 
x = 7 + 4√3

1/x = y and y = 1/x,
so,
= (7 - 4√3)² + (7 + 4√3)² 
= 49-48 - 56√3 + 49 + 48 + 56√3
= 194

​