Integers Chapter Notes | Mathematics Class 6 (Maharashtra Board) PDF Download
| Table of contents |
|
| Introduction |
|
| Integers on a Number Line |
|
| Comparison of Integers |
|
| Integer Operations |
|
Introduction
Integers include positive numbers, negative numbers, and zero. 'Integer' is a Latin word which means 'whole' or 'intact'. This means integers do not include fractions or decimals. Let us learn more about integers, the definition of integers, meaning of integers, and the properties of integers.
What are Integers?
Integers include all whole numbers and negative numbers. This means if we include negative numbers along with whole numbers, we form a set of integers.
or
An integer is a number with no decimal or fractional part and it includes negative and positive numbers, including zero. A few examples of integers are: -5, 0, 1, 5, 8, 97, and 3,043. A set of integers, which is represented as Z, includes:
- Positive Numbers: A number is positive if it is greater than zero. Example: 1, 2, 3, . . .
- Negative Numbers: A number is negative if it is less than zero. Example: -1, -2, -3, . . .
- Zero is defined as neither a negative number nor a positive number. It is a whole number.
Set of Integers
The set of integers is represented by the letter Z and it is written as shown below:
Z = {... -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, ...}
Observe the figure given below to understand the definition of integers.
Integers on a Number Line
A number line is a visual representation of numbers on a straight line. This line is used for the comparison of numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally. Just like other numbers, the set of integers can also be represented on a number line.
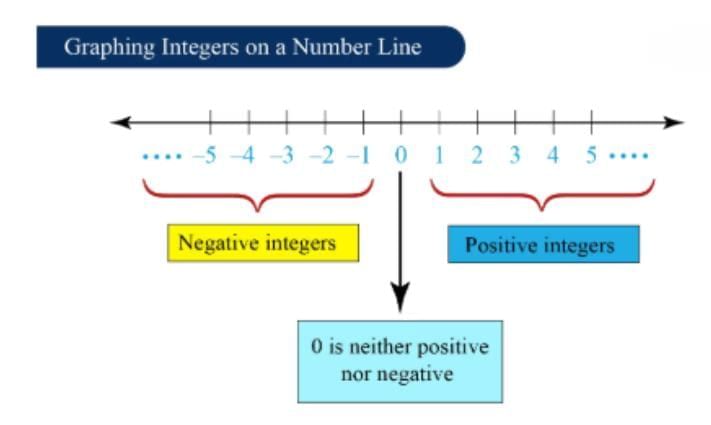
Graphing Integers on a Number Line
Positive and negative integers can be visually represented on a number line. Integers on number line help in performing arithmetic operations. The basic points to keep in mind while placing integers on a number line are as follows:
- The number on the right side is always greater than the number on the left side.
- Positive numbers are placed on the right side of 0, because they are greater than 0.
- Negative numbers are placed on the left side of 0, because they are smaller than 0.
- Zero, which is not positive or negative, is usually kept in the middle.
Comparison of Integers
When comparing counting numbers, we follow the rule that the number to the right on the number line is greater than the number to the left. Since counting numbers are a subset of integers, this rule also applies to all integers. Therefore, for integers as well, the integer positioned to the right on the number line is greater than the one on the left.
Now, see the number line above from which we can make the following observations :
- +5 > +4, since +5 is to the right of +4 on the number line.
- +1 > 0, since +1 is to the right of 0 on the number line.
- 0 > –1, since 0 is to the right of –1 on the number line.
- –1 > –3, since –1 is to the right of –3 on the number line.
From the number line, we can have the following facts :
(i) 0 is less than every positive integer.
(ii) 0 is greater than every negative integer.
(iii) Every negative integer is less than every positive integer.
Arranging Integers in Ascending/ Descending Order
Look at the number line with all integers marked on it; O being the point centrally located, represents the number 0.
The above marking of the number line should not be taken as to mean that –4 and 4 are the end points. Arrows on both sides indicate that there are endless points on both the sides.
In ascending order, we write ... –4 < –3 < –2 < –1 < 0 < 1 < 2 < 3 < 4 < ...
In descending order, we have ... 4 > 3 > 2 > 1 > 0 > –1 > –2 > –3 > –4 > ...
Absolute Value of an Integer
The absolute value of an integer is its numerical value regardless of its sign.We denote it by | | . To write the absolute value of an integer, we omit its sign.
For example,
(a) absolute value of –2 = | –2| = 2
(b) absolute value of –7 = | –7| = 7
(c) absolute value of +3 = | +3| = 3
(d) absolute value of 0 = | 0 | = 0.
Integer Operations
There are some rules for performing these operations of integers. Before we start learning these methods of integer operations, we need to remember a few things.
- If there is no sign in front of a number, it means that the number is positive. For example, 5 means +5.
- The absolute value of an integer is a positive number, i.e., |−2| = 2 and |2| = 2.
(i)Addition of Integers
Adding integers is the process of finding the sum of two or more integers where the value might increase or decrease depending on the integer being positive or negative. The different rules and the possible cases for the addition of integers are given in the following section.
While adding two integers, we use the following rules:
- When both integers have the same signs: Add the absolute values of integers, and give the same sign as that of the given integers to the result.
- When one integer is positive and the other is negative: Find the difference of the absolute values of the numbers and then give the sign of the larger of these numbers to the result.
Example 1: Add the given integers: 2 + (-5)
Ans:
Here, the absolute values of 2 and (-5) are 2 and 5 respectively.
Their difference (larger number - smaller number) is 5 - 2 = 3
Now, among 2 and 5, 5 is the larger number and its original sign “-”.
Hence, the result gets a negative sign, "-”.
Therefore, 2 + (-5) = -3
Example 2: Add the given integers: (-2) + 5
Ans:
Here, the absolute values of (-2) and 5 are 2 and 5 respectively. Their difference (larger number - smaller number) is 5 - 2 = 3. Now, among 2 and 5, 5 is the larger number and its original sign “+”. Hence, the result will be a positive value. Therefore,(-2) + 5 = 3
We can also solve the above problem using a number line. The rules for the addition of integers on the number line are as follows.
- Always start from 0.
- Move to the right side, if the second number is positive.
- Move to the left side, if the second number is negative.
Example 3: Find the value of 5 + (-10) using a number line.
Ans:
In the given problem, the first number is 5 which is positive. So, we start from 0 and move 5 units to the right side.
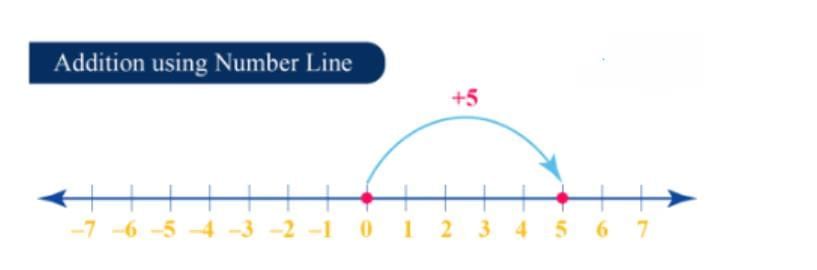
The next number in the given problem is -10, which is negative. We move 10 units to the left side from 5.
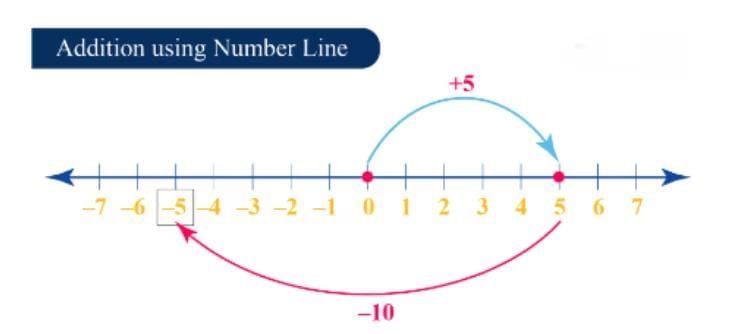
Finally, we reach at -5. Therefore, the value of 5 + (-10) = -5
(ii) Subtraction of Integers
Subtracting Integers is the process of finding the difference between two or more integers where the final value might increase or decrease depending on the integer being positive or negative. The different rules and the possible cases for the subtraction of integers are given in the following section.
Rules of Integers in Subtraction
In order to carry out the subtraction of two integers, we use the following rules:
- Convert the operation into an addition problem by changing the sign of the subtrahend.
- Apply the same rules of addition of integers and solve the problem thus obtained in the above step.
Example 4: Subtract the given integers: 7 - 10
Ans: 7 - 10 can be written as (+ 7) - (+)10
- Convert the given expression into an addition problem and change the sign of the subtrahend, so, we get: 7 + (-10)
- Now, the rules for this operation will be the same as for the addition of two integers.
- Here, the absolute values of 7 and (-10) are 7 and 10 respectively.
- Their difference (larger number - smaller number) is 10 - 7 = 3.
- Now, among 7 and 10, 10 is the larger number and its original sign “-”.
- Hence, the result gets a negative sign, "-”.
- Therefore, 7 - 10 = -3
(iii) Multiplication of Integers
For the multiplication of integers, we use the following rules given in the table. The different rules and the possible cases for the multiplication of integers are given in the following section.
Rules of Integers in Multiplication
In order to carry out the multiplication of two integers, we use the following rules:
Example 5 : Multiply (-6) × 3
Ans: Using the rules of multiplication of integers, when we multiply a positive and negative integer, the product has a negative sign.
Therefore, (-6) × 3 = -18
(iv) Division of Integers
Division of integers means equal grouping or dividing an integer into a specific number of groups. For the divison of integers, we use the rules given in the following table. The different rules and the possible cases for the division of integers are given in the following section
Rules of Integers in Division
In order to carry out the division of two integers, we use the following rules.
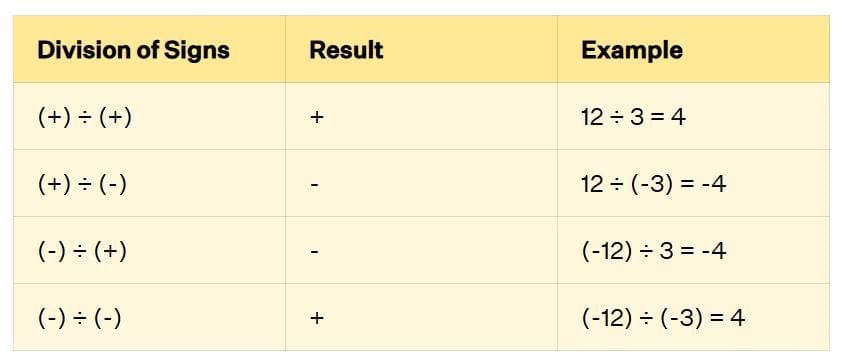
Example 6: Divide (-15) ÷ 3
Ans: Using the rules of division of integers, when we divide a negative integer by a positive integer, the quotient has a negative sign.
Therefore, (-15) ÷ 3 = -5
|
30 videos|112 docs|15 tests
|
FAQs on Integers Chapter Notes - Mathematics Class 6 (Maharashtra Board)
| 1. What are integers and how are they represented on a number line? |  |
| 2. How do we compare integers, and what symbols are used for comparison? | |
| 3. What are the basic operations that can be performed on integers? | |
| 4. Can you explain the rules for adding and subtracting integers? | |
| 5. How can we multiply and divide integers, and what should we consider regarding their signs? | |
Free
,Objective type Questions
,practice quizzes
,Integers Chapter Notes | Mathematics Class 6 (Maharashtra Board)
,Integers Chapter Notes | Mathematics Class 6 (Maharashtra Board)
,study material
,ppt
,Previous Year Questions with Solutions
,Integers Chapter Notes | Mathematics Class 6 (Maharashtra Board)
,shortcuts and tricks
,Summary
,past year papers
,Viva Questions
,Important questions
,mock tests for examination
,Extra Questions
,MCQs
,Exam
,Sample Paper
,Semester Notes
,video lectures
;
Chapter Notes: Integers Free PDF Download
Importance of Chapter Notes: Integers
Chapter Notes: Integers
Chapter Notes: Integers Class 6 Questions
Study Chapter Notes: Integers on the App
|
© EduRev
|
Education Revolution
|
|
