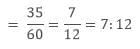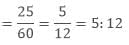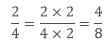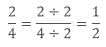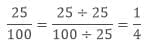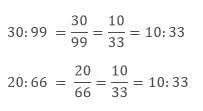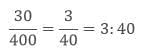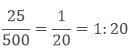Ratio & Proportion Chapter Notes | Mathematics for GCSE/IGCSE - Class 10 PDF Download
| Table of contents |

|
| Ratios |

|
| Equivalent Ratios |

|
| Proportions |

|
| Unitary Method |

|
In this chapter we will be learning about two different things that is ratio and proportion , both of which are applicable in our day to day life.

Ratios
What are Ratios?
- A Ratio is a way to compare two or more quantities.
- It shows how much of one thing there is compared to another.
- Ratios help us understand relationships between different items or groups.
How to Write Ratios
1. Colon Form:
- A ratio can be written using a colon ' : '
- For example, if there are 4 cats and 2 dogs,
the ratio of cats to dogs is written as 4:2.
2. Fraction Form:
- The same ratio can also be expressed as a fraction.
- So, 4:2 can be written as 4/2, which simplifies to 2/1.
Example 1: If there are 35 boys and 25 girls in a class, then what is the ratio of
1. Number of boys to total students
2. Number of girls to total students.
Sol:
In the ratio, we want the total number of students.
Total number of students = Number of boys + Number of girls
35 + 25 = 601. Ratio of number of boys to total number of students
2. The ratio of the number of girls to the total number of students
EduRev Tip:
- The units must be the same to compare two quantities.
If we have to compare two quantities with different units then we need to convert them in the same unit. then only they can be compared using ratio.
Example 2: What is the ratio of the height of Raman and Radha if the height of Raman is 175 cm and Radha is 1.35 m?
Sol: In this case we will first convert the heights into same unit (cm) and then will proceed.
- The unit of the height of Raman and Radha is not same so convert them in the same unit.
- Height of Radha is 1.35 m = 1.35 × 100 cm = 135 cm
- The ratio of the height of Raman and Radha
Equivalent Ratios
- If we multiply or divide both the numerator and denominator by the same number then we get the equivalent ratio.
- There could be so many equivalent ratios of the same ratio.
- In the case of equivalent ratios only their value changes but they represent the same portion of the quantity.
Example: Find two equivalent ratios of 2/4.
Sol:
- To get the equivalent ratio we multiply both the numerator and denominator with 2.
- To get another equivalent ratio we divide both the numerator and denominator with 2.
- From the above figure, we can see that in all the equivalent ratios only the number of equal parts is changing but all the ratios are representing the half part of the circle only.
Lowest Form of the Ratio
- If there is no common factor of numerator and denominator except one then it is the lowest form of the ratio.
- Example: 3/8 , 2/7 etc.
Example 1: Find the lowest form of the ratio 25: 100.
Sol: Firstly write the ratio into fractional form i.e 25/100
- The common factor of 25 and 100 is 25, so divide both the numerator and denominator with 25.
- Hence the lowest ratio of 25: 100 is 1: 4.
Proportions
What are Proportions?
- A proportion is an equation that states that two ratios are equal.
- It shows how two quantities relate to each other.
How to write Proportions?
A proportion can be written as: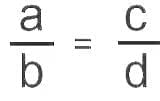
- We write it as a: b : : c: d or a: b = c: d and reads as “a is to b as c is to d”.
- If the two ratios are not equal then these are not in proportion.
Example 1: If a man runs at a speed of 20 km in 2 hours then with the same speed would he be able to cross 40 km in 4 hours?
Sol: We can use simple comparison to solve this question
- Here the ratio of the distances given is 20/40 = 1/2 = 1: 2
- And the ratio of the time taken by them is also 2/4 = 1/2 = 1: 2
- Hence the four numbers are in proportion.
- We can write them in proportion as 20: 40 : : 2: 4
- And reads as “20 is to 40 as 2 is to 4”.
Extreme Terms and Middle Terms of Proportion
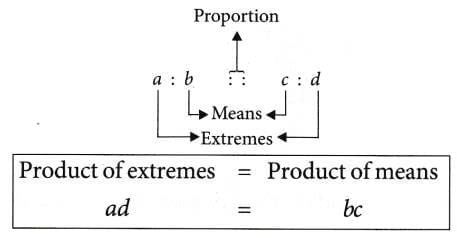
- The first and the fourth term in the proportion are called extreme terms
- The second and third terms are called the Middle or the Mean Terms.
- In this statement of proportion, the four terms which we have written in order are called the Respective Terms.
Example 1: Check whether the terms 30 , 99 ; 20 ,66 are in proportion or not.
Sol: Yes, the given terms are in proportion
- To check the numbers are in proportion or not we have to equate the ratios.
- As both the ratios are equal so the four terms are in proportion.
- 30: 99 :: 20: 66
Example 2: Find the ratio 30 cm to 4 m is proportional to 25 cm to 5 m or not?
Sol: No, the ratios are not in proportion.
- As the unit is different so we have to convert them into the same unit.
- 4 m = 4 × 100 cm = 400 cm
- The ratio of 30 cm to 400 cm is
- 5 m = 5 × 100 cm = 500 cm
- Ratio of 25 cm to 500 cm is
- Here the two ratios are not equal so these ratios are not in proportion.
- 3: 40 ≠ 1: 20
Did You Know:
- If you have to see if two ratios are equal, you can just cross-multiply.
- For example, If you have to check the ratios 2:3 and 4:6
- Cross-multiply:
- 2×6=12
- 3×4=12
- Since both products are equal, we say that 2:3 is proportional to 4:6
Unitary Method
If we find the value of one unit then calculate the value of the required number of units then Unitary method is used.
Example 1: If the cost of 3 books is 320 Rs. then what will be the cost of 6 books?

Sol:
- Cost of 3 books = Rs. 320
- Cost of 1 book = 320/3 Rs.
- Cost of 6 books = (320/3) × 6 = 640 Rs.
- Hence, the cost of 6 books is Rs. 640.
Example 2: If the cost of 20 toys is Rs. 4000 then how many toys can be purchased for Rs. 6000?
Sol:
- In Rs. 4000, the number of toys can be purchased = 20
- In Rs. 1, the number of toys can be purchased = Rs. 20/4000
- Therefore, in Rs. 6000, the number of toys can be purchased = (20/4000) × 6000 = 30
- Hence, 30 toys can be purchased by Rs. 6000.
|
85 videos|394 docs|60 tests
|
FAQs on Ratio & Proportion Chapter Notes - Mathematics for GCSE/IGCSE - Class 10
| 1. What is a ratio, and how is it expressed? |  |
| 2. What are equivalent ratios? |  |
| 3. How do you determine if two ratios are in proportion? |  |
| 4. What is the unitary method, and how is it used in solving problems? |  |
| 5. Can you give an example of using ratios in everyday life? |  |