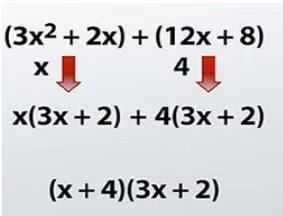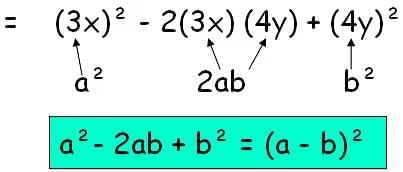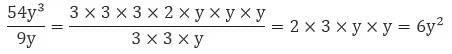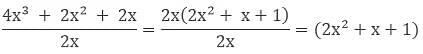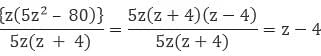Factorisation of Algebraic expressions Chapter Notes | Mathematics Class 8 (Maharashtra Board) PDF Download
| Table of contents |

|
| Introduction |

|
| What is Factorisation? |

|
| Division of Algebraic Expressions |

|
| Division of Algebraic Expressions Continued (Polynomial ÷ Polynomial) |

|
Introduction
Factors of Natural Numbers
Factors are the pair of natural numbers which give the resultant number.
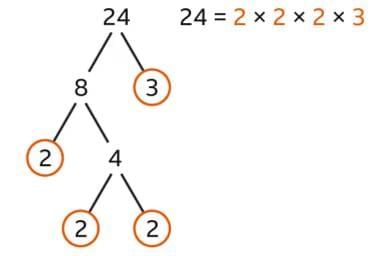
Example: Number 24 can be reduced to its factors as follows
24 = 12 × 2 = 6 × 4 = 8 × 3 = 2 × 2 × 2 × 3 = 24 × 1
Hence, 1, 2, 3, 4, 6, 8, 12 and 24 are the factors of 24.
Prime Factor Form
If we write the factors of a number in such a way that all the factors are prime numbers then it is said to be a prime factor form.
Example
The prime factor form of 24 is
24 = 2 × 2 × 2 × 3.
Here, 2 and 3 are prime numbers (or prime factors of the number 24).
Factors of Algebraic Expressions
Like any natural number, an algebraic expression is also the product of its factors. In the case of algebraic expression, it is said to be an irreducible form instead of prime factor form.
Example
7pq = 7 × p × q =7p × q = 7q × p = 7 × pq
These are the factors of 7pq but the irreducible form of it is
7pq = 7 × p × q
Example
2x (5 + x)
Here the irreducible factors are
2x (5 + x) = 2 × x × (5 + x)
What is Factorisation?
The factors of an algebraic expression could be anything like numbers, variables and expressions.
As we have seen above that the factors of algebraic expression can be seen easily but in some case like 2y + 4, x2 + 5x etc. the factors are not visible, so we need to decompose the expression to find its factors.
1. Method of Common Factors
In this method, we have to write the irreducible factors of all the terms
Then find the common factors amongst all the irreducible factors.
The required factor form is the product of the common term we had chosen and the leftover terms.
Example
2. Factorisation by Regrouping Terms
Sometimes it happens that there is no common term in the expressions then
We have to make the groups of the terms.
Then choose the common factor among these groups.
Find the common binomial factor and it will give the required factors.
Example: Factorise 3x2 + 2x + 12x + 8
Sol: First, we have to make the groups then find the common factor from both the groups.
Now the common binomial factor i.e. (3x + 2) has to be taken out to get the two factors of the expression.
3. Factorisation Using Identities
Remember some identities to factorise the expression
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(a + b) (a – b) = a2 – b2
We can see the different identities from the same expression.
(2x + 3)2 = (2x)2+ 2(2x) (3) + (3)2
⇒ 4x2 + 12x + 9
(2x - 3)2 = (2x)2 – 2(2x)(3) + (3)2
⇒ 4x2 -12x + 9
(2x + 3) (2x - 3) = (2x)2 – (3)2
⇒ 4x2 - 9
Example 1: Factorise x – (2x – 1)2 using identity.
Sol: This is using the identity (a + b) (a – b) = a2 – b2
x2- (2x - 1)2 = [(x + (2x - 1))] [x – (2x-1))]
= (x + 2x - 1) (x – 2x + 1)
= (3x – 1) (- x + 1)
Example 2: Factorize 9x² - 24xy + 16y² using identity.
Sol:
1. First, write the first and last terms as squares.
9x² - 24xy + 16y²
= (3x)2 – 24xy + (4y)2
2. Now split the middle term.
= (3x)2 – 2(3x) (4y) + (4y)2
3. Now check it with the identities
4. This is (3x – 4y)2
5. Hence the factors are (3x – 4y) (3x – 4y).
Example : Factorise x2 + 10x + 25 using identity.
Sol:
x2 + 10x + 25
= (x)2 + 2(5) (x) + (5)2
We will use the identity (a + b) 2 = a2 + 2ab + b2 here.
Therefore,x2 + 10x + 25 = (x + 5)2
4. Factors of the form ( x + a) ( x + b)
(x + a) (x + b) = x2 + (a + b) x + ab.
Example: Factorise x2 + 3x + 2.
Sol: If we compare it with the identity (x + a) (x + b) = x2 + (a + b) x +ab
We get to know that (a + b) = 3 and ab = 2.
This is possible when a = 1 and b = 2.
Substitute these values into the identity,
x2 + (1 + 2) x + 1 × 2
(x + 1) (x + 2)
Division of Algebraic Expressions
Division is the inverse operation of multiplication.
1. Division of a Monomial by another Monomial
Write the irreducible factors of both the monomials
Cancel out the common factors.
The balance is the answer to the division.
Example: Solve 54y3 ÷ 9y
Sol: Write the irreducible factors of the monomials
54y3 = 3 × 3 × 3 × 2 × y × y × y
9y = 3 × 3 × y
2. Division of a Polynomial by a Monomial
Write the irreducible form of the polynomial and monomial both.
Take out the common factor from the polynomial.
Cancel out the common factor if possible.
The balance will be the required answer.
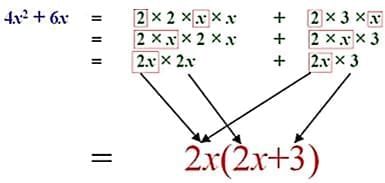
Example: Solve 4x3 + 2x2 + 2x ÷ 2x.
Sol: Write the irreducible form of all the terms of polynomial
4x3 + 2x2 + 2x
= 4(x) (x) (x) + 2(x) (x) + 2x
Take out the common factor i.e.2x
= 2x (2x2 + x + 1)
Division of Algebraic Expressions Continued (Polynomial ÷ Polynomial)
In the case of polynomials we need to reduce them and find their factors by using identities or by finding common terms or any other form of factorization. Then cancel out the common factors and the remainder will be the required answer.
Example: Solve z (5z2 – 80) ÷ 5z (z + 4)
Sol: Find the factors of the polynomial
= z (5z2 – 80)
= z [(5 × z2) – (5 × 16)]
= z × 5 × (z2 – 16)
= 5z × (z + 4) (z – 4) [using the identity a2 – b2 = (a + b) (a – b)]
Some Common Errors
While adding the terms with same variable students left the term with no coefficient but the variable with no coefficient means 1.
2x + x + 3 = 3x + 3 not 2x +3
We will consider x as 1x while adding the like terms.
If we multiply the expressions enclosed in the bracket then remember to multiply all the terms.
2(3y + 9) = 6y + 18 not 6y + 9
We have to multiply both the terms with the constant.
If we are substituting any negative value for the variables then remember to use the brackets otherwise it will change the operation and the answer too.
If x = – 5
Then 2x = 2(-5) = -10
Not, 2 – 5 = - 3
While squaring of the monomial we have to square both the number and the variable.
(4x)2 = 16x2 not 4x2
We have to square both the numerical coefficient and the variable.
While squaring a binomial always use the correct formulas.
(2x + 3)2 ≠ 4x2+ 9 But (2x + 3)2 = 4x2 + 12x + 9
While dividing a polynomial by a monomial remember to divide each term of the polynomial in the numerator by the monomial in the denominator.
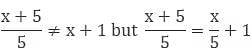
|
20 videos|110 docs|12 tests
|
FAQs on Factorisation of Algebraic expressions Chapter Notes - Mathematics Class 8 (Maharashtra Board)
| 1. What is the definition of factorisation in algebra? |  |
| 2. Why is factorisation important in solving algebraic equations? |  |
| 3. What are the common methods used for factorising algebraic expressions? |  |
| 4. How do you divide algebraic expressions, particularly polynomials? |  |
| 5. What is the significance of understanding division of algebraic expressions in advanced mathematics? |  |