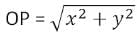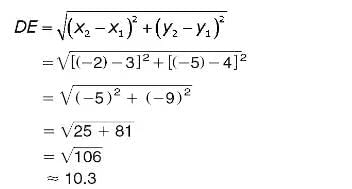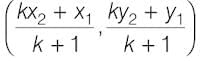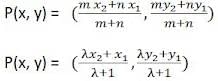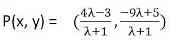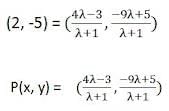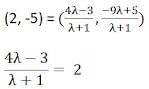Co-ordinate Geometry Chapter Notes | Mathematics Class 10 (Maharashtra SSC Board) PDF Download
| Table of contents |

|
| What is a Coordinate System? |

|
| Distance Formula |

|
| Section Formula |

|
| Mid -Point Formula |

|
| Some Solved Questions |

|
What is a Coordinate System?
A Coordinate System is a mathematical framework used to determine the position or location of points in space. It provides a way to describe the position of objects or points using numerical values called coordinates.
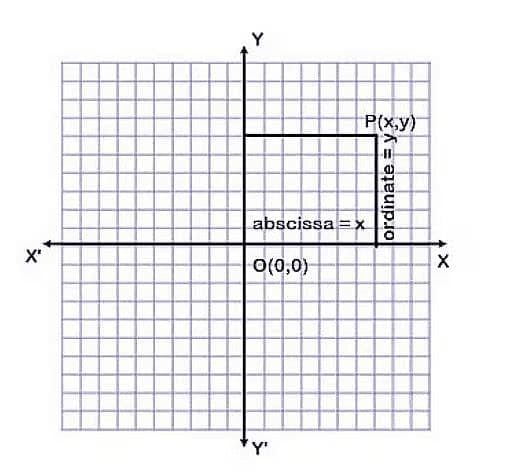
- As shown in the figure, the line XOX′ is known as the X-axis, and YOY′is known as the Y-axis.
- The point O is called the origin. For any point P (x y), the ordered pair(x,y) is called the coordinate of point P.
- The distance of a point from the Y-axis is called its abscissa and the distance of a point from the X-axis is called its ordinate.
Distance between Two Points Using Pythagoras' Theorem
Let P(x1, y1) and Q(x2, y2) be any two points on the cartesian plane.
Draw lines parallel to the axes through P and Q to meet at T.
ΔPTQ is right-angled at T.
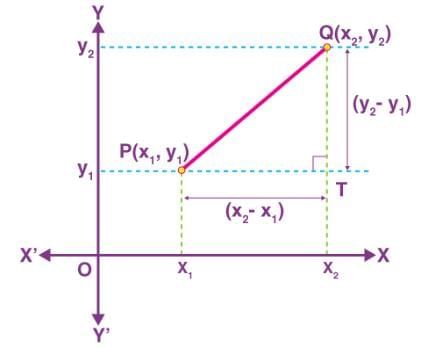
By Pythagoras Theorem,
PQ2 = PT2 + QT2
= (x2 – x1)2 + (y2 – y1)2
PQ = √[x2 – x1)2 + (y2 – y1)2]
Distance Formula
Distance between any two points (x1, y1) and (x2, y2) is given by
d = √[x2 – x1)2+(y2 – y1)2]
Where d is the distance between the points (x1,y1) and (x2,y2).
Note:The distance of any point P(x,y) from the origin O(0,0) is given by:
Example 1: Find the distance between the points D and E, in the given figure.
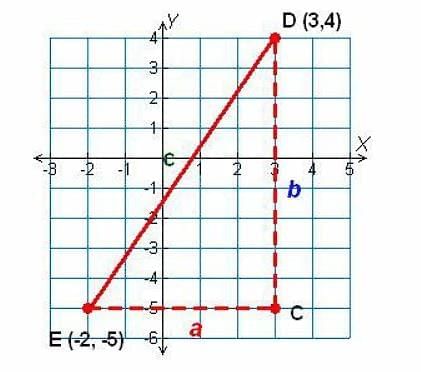
Solution:
Example 2: What is the distance between two points (2, 3) and (-4, 5) using the distance formula?
Sol: The distance formula is used to calculate the distance between two points in a coordinate plane. It is given as:
d = √[(x2 - x1)² + (y2 - y1)²]
Using this formula, we can find the distance between the points (2, 3) and (-4, 5) as follows:
d = √[(-4 - 2)² + (5 - 3)²]
d = √[(-6)² + (2)²]
d = √[36 + 4]
d = √40
d = 6.32 (approx.)
Therefore, the distance between the points (2, 3) and (-4, 5)is approximately 6.32 units.
Section Formula
Let P (x,y) be a point on the line segment joining A(x1, y1) and B(x2, y2) such that it divides AB internally in the ratio m:n. The coordinates of the point P are given by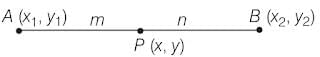
 This is known as the Section Formula.
This is known as the Section Formula.
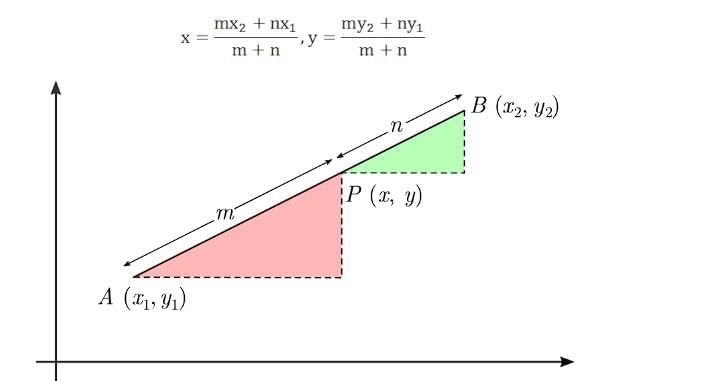
Note:
(i) If the point P divides the line segment joining A(x1, y1) and B(x2, y2) internally in the ratio k:1, its coordinates are given by:
Example 2: In what ratio does the point (2,- 5) divide the line segment joining the points A(-3, 5) and B(4, -9)?
Sol: Let the ratio be λ : 1
We have put m = λ and n = 1
or
But, coordinates of point is given as p(2,-5)
But, coordinates of point is given as p(2,-5)
4λ - 3 = 2(λ + 1)
⇒ 4λ = 2λ + 2 + 3⇒ 2λ = 5
⇒ λ = 5/2The required ratio is 5:2.
Mid -Point Formula
The mid-point of the line joining A(x1, y1) and B(x2, y2) is given as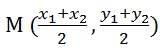
Example 3:Suppose we have two points A(2, 4) and B(6, 8). We want to find the midpoint of the line segment AB.
Sol:Using the midpoint formula:Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
= ((2 + 6) / 2, (4 + 8) / 2)
= (8 / 2, 12 / 2)
= (4, 6)
Therefore, the midpoint of the line segment AB is M(4, 6).
Some Solved Questions
Q1: Find the distance between the points (3, 5) and (-2, -1) using the distance formula.
Sol:
Using the distance formula:
d = √[(x2 - x1)² + (y2 - y1)²]
Substituting the coordinates:
d = √[(-2 - 3)² + (-1 - 5)²]
d = √[(-5)² + (-6)²]
d = √[25 + 36]
d = √61
Therefore, the distance between the points (3, 5) and (-2, -1) is √61 units.
Q2: Find the coordinates of the midpoint of the line segment joining the points (-3, 2) and (5, -4).
Sol:
Using the midpoint formula:
Midpoint = ((x1 + x2) / 2, (y1 + y2) / 2)
Substituting the coordinates:
Midpoint = ((-3 + 5) / 2, (2 + (-4)) / 2)
Midpoint = (2 / 2, -2 / 2)
Midpoint = (1, -1)
Therefore, the midpoint of the line segment joining (-3, 2) and (5, -4) is (1, -1).
|
26 videos|208 docs|38 tests
|
FAQs on Co-ordinate Geometry Chapter Notes - Mathematics Class 10 (Maharashtra SSC Board)
| 1. What is a coordinate system and why is it important in geometry? |  |
| 2. How is the distance formula derived and what does it calculate? |  |
| 3. What is the section formula and how is it applied in coordinate geometry? |  |
| 4. Can you explain the mid-point formula and its significance? |  |
| 5. What are some common applications of coordinate geometry in real life? |  |