Integers, Rational Numbers, and the Coordinate Plane Chapter Notes | Preparation for EmSAT Grade 6 PDF Download
| Table of contents |

|
| Introduction |

|
| Integers |

|
| Rational numbers |

|
| Comparing rational numbers |

|
| Coordinate Plane |

|
Introduction
Integers, rational numbers, and the coordinate plane are foundational concepts in mathematics. Integers include positive and negative whole numbers and zero, represented on a number line for comparison and ordering. Rational numbers, expressible as fractions of integers, include integers, fractions, and decimals, while irrational numbers cannot be written as fractions. Comparing and ordering rational numbers often involves number lines or converting to common forms. The coordinate plane, formed by intersecting x- and y-axes, allows plotting points using ordered pairs, enabling visualization of numerical relationships.
Integers
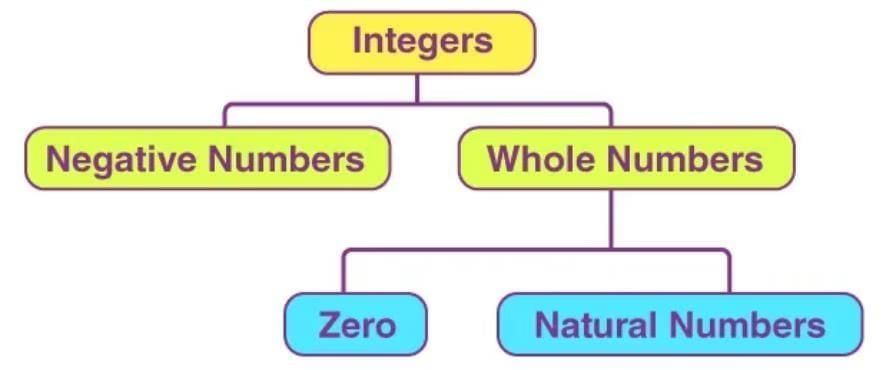
- Integers include all whole numbers (0, 1, 2, 3, …), negative numbers (…, -3, -2, -1), and zero.
- Negative integers are numbers less than zero (e.g., -1, -2, -3).
- Positive integers are numbers greater than zero (e.g., 1, 2, 3).
- Zero is an integer that is neither positive nor negative.
- Example: The numbers …, -4, -3, -2, -1, 0, 1, 2, 3, 4, … are all integers.
Representation of Integers on a Number Line

- Draw a horizontal line and mark a point labelled ‘O’ as zero.
- Mark points at equal intervals to the right of zero as 1, 2, 3, …
- Mark points at equal intervals to the left of zero as -1, -2, -3, …
- Each integer corresponds to a point on the line, with negative numbers to the left and positive numbers to the right.
- Opposites, like 1 and -1, are equidistant from zero in opposite directions.
Ordering of Integers
- On a number line, numbers increase from left to right.
- Positive integers are greater than negative integers (e.g., 5 > -3).
- Zero is greater than all negative integers but less than all positive integers.
- The further a number is to the right of zero, the larger its value.
- The further a number is to the left of zero, the smaller its value.
- To compare integers, place them on a number line and observe their positions.
- Example: Temperatures in Amritsar (-2°C), Shimla (-4°C), and Chandigarh (0°C) are ordered as -4°C < -2°C < 0°C, showing Shimla is coldest and Chandigarh is warmest.

Absolute Value of an Integer
- The absolute value of an integer is its numerical value without its sign, denoted by |n|.
- For a positive integer, the absolute value is the number itself (e.g., |5| = 5).
- For a negative integer, the absolute value is its positive counterpart (e.g., |-5| = 5).
- The absolute value of zero is zero (|0| = 0).
- Formula: |n| = n if n ≥ 0; |n| = -n if n < 0.
- Example: Evaluate |-33|, -|990|, |-111|, |0|.
- |-33| = 33
- -|990| = -990 (since |990| = 990)
- |-111| = 111
- |0| = 0
Rational numbers
What are rational numbers?
- A rational number is any number that can be made by dividing two integers. Remember that integers can be positive, negative, or zero, but they cannot have fractional or decimal parts.
- All rational numbers can be written in the form p/q where p and q are integers and q is not zero.
- 2/3 is a rational number.
- – 5 is a rational number because it can be written as – 5/1.
- 4.75 is a rational number because it can be written as 19/4.
- – 0.36 is a rational number because it can be written as – 9/25.
- 1.18 is a rational number because it can be written as 13/11.
- Integers, fractions, terminating decimals, and repeating decimals are all rational numbers.
What are irrational numbers?
Any number that is not rational is irrational. An irrational number cannot be made by dividing two integers. Irrational numbers that are written as decimals never terminate and never repeat.
- √2 is an irrational number because it cannot be written as a fraction. √2 is 1.41421356237…
- 𝜋 is an irrational number because it cannot be written as a fraction. 𝜋 is 3.14159265358…
Comparing rational numbers
Rational numbers can be written as fractions or decimals. For example, the following numbers are all rational: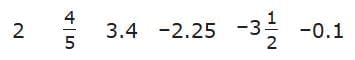 Look at each rational number on a number line. Notice that the negative numbers are to the left of zero and the positive numbers are to the right of zero. The farther right you go, the greater the value.
Look at each rational number on a number line. Notice that the negative numbers are to the left of zero and the positive numbers are to the right of zero. The farther right you go, the greater the value.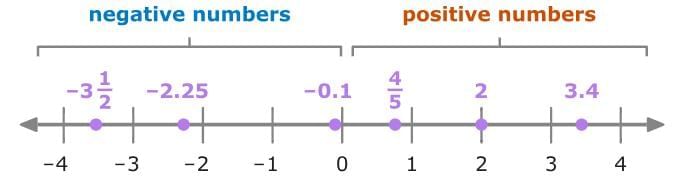
How do you compare rational numbers?
- When you compare rational numbers, it often helps to use a number line.
- It can also help to write both numbers in the same form. You can write them both as fractions or as decimals. If the numbers are fractions, you can write them to have a common denominator to make them easier to compare.
- For Example: Compare 0.2 and – 0.4.
Since 0.2 is positive and – 0.4 is negative, 0.2 is greater than – 0.4. The number 0.2 is farther right on the number line. So, 0.2 > –0.4.
So, 0.2 > –0.4.
How do you order rational numbers?
- You can order rational numbers using what you know about comparing rational numbers.
- For Example: Put these rational numbers in order from least to greatest:
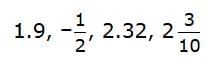 First, find the smallest number. Since negative numbers are always less than positive numbers,
First, find the smallest number. Since negative numbers are always less than positive numbers, 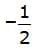 is the smallest number.
is the smallest number.
Now, you are left with three positive numbers. Look at the whole number parts. Since 1 is less than 2, 1.9 comes next.
Last, look at the remaining numbers. To compare 2.32 and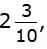 write both numbers in the same form. Write
write both numbers in the same form. Write 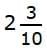 as a decimal.
as a decimal.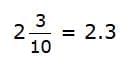 Since 2.3 is less than 2.32,
Since 2.3 is less than 2.32, 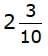 comes next.
comes next.
That leaves 2.32 as the largest number.
So, these are the rational numbers in order from least to greatest: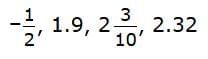
Coordinate Plane
A coordinate plane is a grid formed by two number lines. The horizontal number line is called the x-axis. The vertical number line is called the y-axis. The two axes meet at the origin. The origin is at zero on both number lines.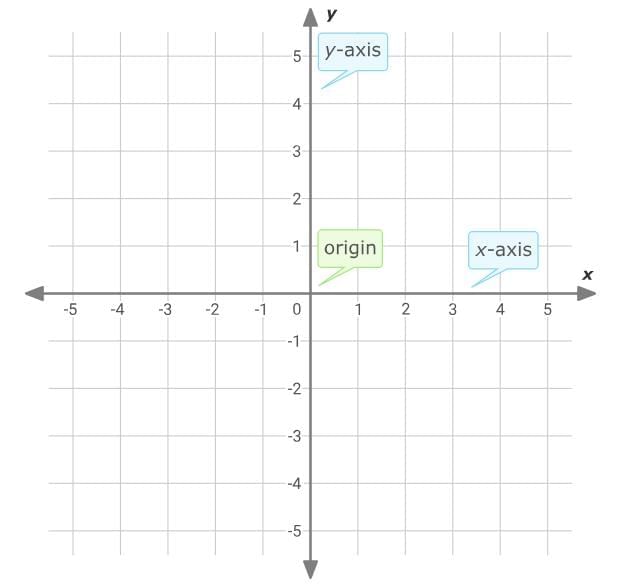 The axes divide the coordinate plane into four quadrants. The quadrants are named using Roman numerals.
The axes divide the coordinate plane into four quadrants. The quadrants are named using Roman numerals.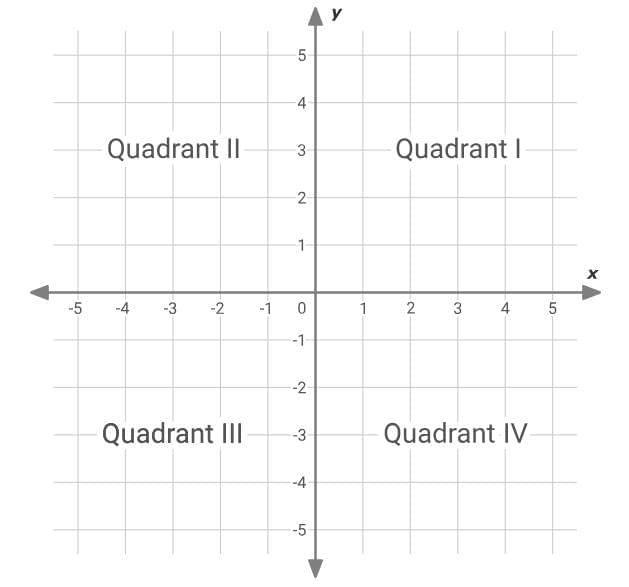
How do you plot a point on the coordinate plane?
- Each location on the coordinate plane is represented by an ordered pair. An ordered pair has two numbers written in the form (x,y). The first number is the x-coordinate. It tells you the location of the point on the x-axis. The second number is the y-coordinate. It tells you the location of the point on the y-axis.
- To plot a point on the coordinate plane, follow these steps:
- Start at the origin.
- Move left or right to find the x-coordinate on the x-axis.
- Move up or down to find the y-coordinate on the y-axis. Plot a point at this location.
- For Example: Let's try it for (4, 2).
Start at the origin. Then, find the x-coordinate on the x-axis. Since the x-coordinate in (4, 2) is 4, move to the right 4 spaces.
Then, find the x-coordinate on the x-axis. Since the x-coordinate in (4, 2) is 4, move to the right 4 spaces.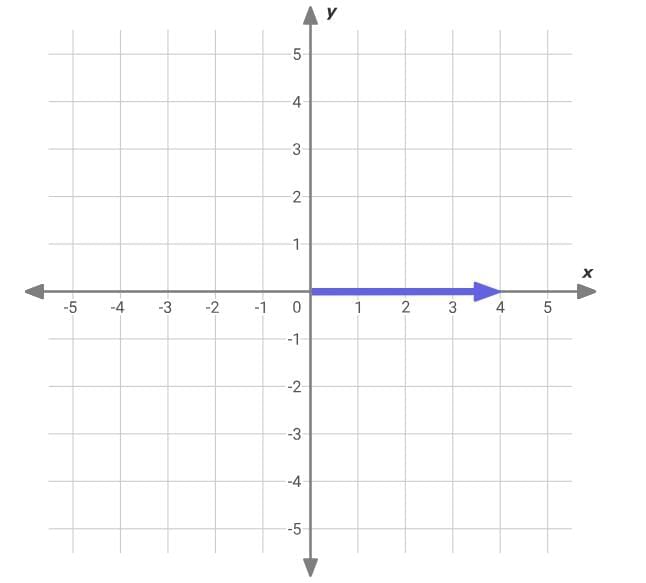 Now, find the y-coordinate on the y-axis. Since the y-coordinate in (4, 2) is 2, move up 2 spaces. Plot a point at this location.
Now, find the y-coordinate on the y-axis. Since the y-coordinate in (4, 2) is 2, move up 2 spaces. Plot a point at this location.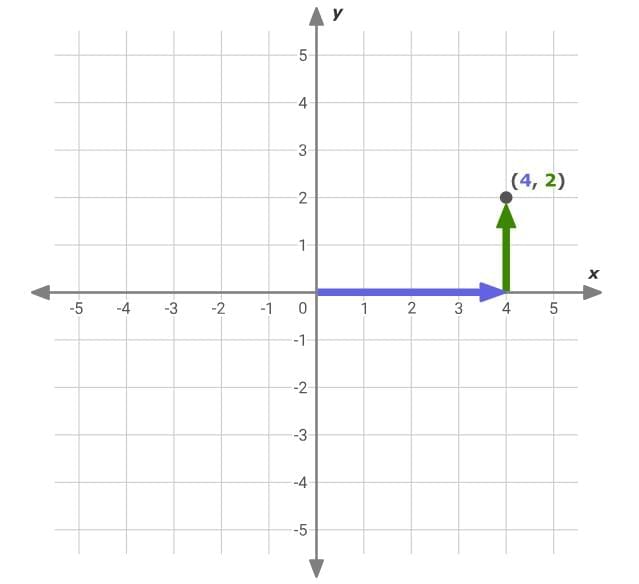
|
237 docs|47 tests
|
FAQs on Integers, Rational Numbers, and the Coordinate Plane Chapter Notes - Preparation for EmSAT Grade 6
| 1. What are integers, and how do they differ from rational numbers? |  |
| 2. How can I compare rational numbers effectively? |  |
| 3. What is the coordinate plane, and what are its components? |  |
| 4. How do I plot points on the coordinate plane? |  |
| 5. Why is understanding rational numbers important in real life? |  |



















