Grade 6 Exam > Grade 6 Notes > Mathematics for Grade 6 > Chapter Notes: Powers and Exponents
Powers and Exponents Chapter Notes | Mathematics for Grade 6 PDF Download
Introduction
Exponents are a simple way to show repeated multiplication of a number. For example, in 5³, the exponent 3 means you multiply 5 three times. Powers of 10, like 100 or 0.01, use exponents to represent numbers with zeros or decimal places. The exponent tells you how many zeros or decimal places there are. This guide explains exponents, including positive and negative powers of 10, with clear examples to make them easy to understand.
Exponents
What is an exponent?
- An exponent is a number that shows repeated multiplication.
- For Example: In 53, the exponent is 3. This tells you to multiply three 5s.
53 = 5 × 5 × 5
In 53, 3 is the exponent, and 5 is the base.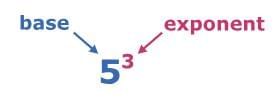
Exponents with powers of 10
- Powers of 10 are numbers like 10, 100, and 1,000. They have a 1 followed by one or more zeros. Powers of 10 can always be written with an exponent.
- Look at the table. Do you see a pattern in the number of zeros and the exponent?
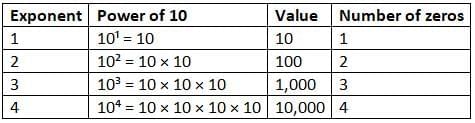 The exponent matches the number of zeros! You can use that pattern to write powers of 10.
The exponent matches the number of zeros! You can use that pattern to write powers of 10. - For Example: How would you write 1,000,000 as a power of 10?
There are 6 zeros, so the exponent will be 6.
1,000,000 = 106
You can go the other direction, too. Let's try it with 1012. There will be 12 zeros.
1012 = 1,000,000,000,000
That's a trillion!
Powers of 10
What are powers of 10?
- Powers of 10 are numbers like 10, 100, and 1,000. Powers of 10 can always be written with an exponent.
- Look at the table. Do you see a pattern in the number of zeros and the exponent?
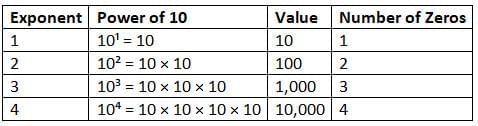 The exponent matches the number of zeros! You can use that pattern to write powers of 10.
The exponent matches the number of zeros! You can use that pattern to write powers of 10. - For Example: Let's try it with 1,000,000.
There are 5 zeros, so the exponent is 5.
100,000 = 105
You can use the pattern to evaluate powers of 10, too. Let's try it with 108. There will be 8 zeros.
108 = 100,000,000
You can check the answer by using repeated multiplication.
Did you know?
1 is a power of 10? It is 100!
Powers of 10 with negative exponents
- You can also have powers of ten with negative exponents. For example, 0.01 is a power of 10. You can write it as 10–2.
- You can write a negative exponent as a positive exponent under a numerator of 1. So, 10–2 is the same as
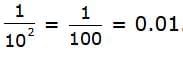 .
. - Look at the table. Do you see a pattern in the number of decimal places and the exponent?
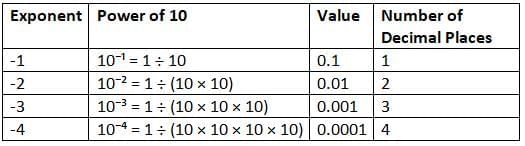 The exponent matches the number of decimal places! You can use that pattern to write powers of 10 with negative exponents.
The exponent matches the number of decimal places! You can use that pattern to write powers of 10 with negative exponents. - For Example: Let's try it with 10–6.
The exponent is –6. There will be 6 decimal places.
10–6 = 0.000001
You can use the pattern in the other direction, too. Let's try it with 0.0000001.
There are 7 decimal places. The exponent will be –7.
0.0000001 = 10–7
Tip: Remember, for a positive exponent, count the number of zeros. For a negative exponent, count the number of decimal places.
The document Powers and Exponents Chapter Notes | Mathematics for Grade 6 is a part of the Grade 6 Course Mathematics for Grade 6.
All you need of Grade 6 at this link: Grade 6
|
36 videos|76 docs|14 tests
|
FAQs on Powers and Exponents Chapter Notes - Mathematics for Grade 6
| 1. What are exponents, and how are they used in mathematics? |  |
Ans. Exponents are a way to express repeated multiplication of a number by itself. For example, 2³ means 2 multiplied by itself three times, which equals 8. Exponents are used in various mathematical operations, including simplifying expressions and solving equations.
| 2. What are the powers of 10, and why are they important? |  |
Ans. Powers of 10 are expressions where 10 is raised to an exponent, such as 10² (which equals 100) or 10⁻¹ (which equals 0.1). They are important in scientific notation, where large or small numbers can be expressed succinctly, making them easier to read and work with in calculations.
| 3. How do you simplify expressions that involve exponents? |  |
Ans. To simplify expressions with exponents, you can use the laws of exponents, such as multiplying powers (aᵐ × aⁿ = aᵐ⁺ⁿ), dividing powers (aᵐ ÷ aⁿ = aᵐ⁻ⁿ), and raising a power to a power ( (aᵐ)ⁿ = aᵐⁿ). Following these rules helps to reduce complex expressions to simpler forms.
| 4. Can you provide examples of how to convert numbers into scientific notation using powers of 10? |  |
Ans. To convert a number into scientific notation, you express it as a product of a number between 1 and 10 and a power of 10. For example, the number 5000 can be written as 5 × 10⁴, while 0.0045 can be expressed as 4.5 × 10⁻³. This format is useful for managing very large or very small numbers.
| 5. What are some real-life applications of exponents and powers of 10? |  |
Ans. Exponents and powers of 10 have many real-life applications. They are used in fields such as science and engineering to express large quantities, such as the speed of light (approximately 3 × 10⁸ meters per second) or the size of atoms (on the order of 10⁻¹⁰ meters). They also appear in finance for calculating compound interest and in computer science for measuring data storage.
Related Searches




















