Grade 6 Exam > Grade 6 Notes > Mathematics for Grade 6 > Chapter Notes: Distributive Property
Distributive Property Chapter Notes | Mathematics for Grade 6 PDF Download
| Table of contents |

|
| Introduction |

|
| What is the distributive property? |

|
| The distributive property with variables |

|
| Using the distributive property to multiply large numbers |

|
Introduction
The distributive property is a math rule that helps you multiply a number by a sum or difference inside parentheses. Instead of solving inside the parentheses first, you multiply the number outside by each term inside and then add or subtract the results. It works for numbers, variables, and even large numbers, making calculations easier. This guide explains the distributive property with clear examples to show how it simplifies multiplication in different situations.
What is the distributive property?
- Let's say you want to find 5(6 + 8). You could use the order of operations to solve by adding the numbers in parentheses first.
- 5(6 + 8)
- 5(14)
- 70
- Or you could use the distributive property. Multiply the number outside of the parentheses by each number inside of the parentheses. Then add those products.
Look at the steps below:- 5(6 + 8)
- 5(6) + 5(8)
- 30 + 40
- 70
- So, 5(6 + 8) = 70!
- The distributive property works with subtraction in the parentheses, too.
- 8(10 – 4)
- 8(10) – 8(4)
- 80 – 32
- 48
- Check your work with the order of operations:
- 8(10 – 4)
- 8(6)
- 48
- So, 8(10 – 4) = 48!
The distributive property with variables
- The distributive property is useful when simplifying expressions with variables. When using variables, you may not be able to do the operation inside the parentheses first.
- For Example: 8(y + 4z)
The y and 4z cannot be combined. They are not like terms.
8(y) + 8(4z)
8y + 32z
Remember to multiply, or distribute, the 8 to each term inside the parentheses.
So, 8(y + 4z) = 8y + 32z!
Using the distributive property to multiply large numbers
- You can use the distributive property to help multiply large numbers.
- For Example: Let's try it with 6×57. First, split 57 up into smaller pieces.
6 × 57
6 × (50 + 7)
Then use the distributive property to solve!
6(50 + 7)
6(50) + 6(7)
300 + 42
342
You can use area models to see why this works. The model below shows 6 × 57. You can also show 6 × 57 as 6 × (50 + 7).
You can also show 6 × 57 as 6 × (50 + 7).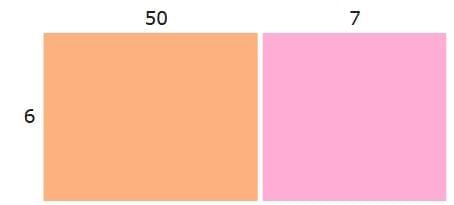 Multiply the 6 by 50 and by 7.
Multiply the 6 by 50 and by 7.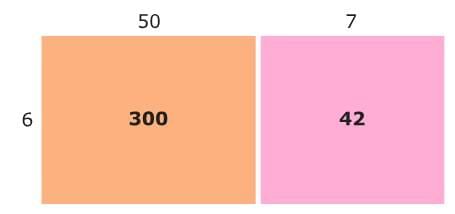 Then add to find the total area.
Then add to find the total area.
300 + 42 = 342
So, 6 × 57 = 342!
The document Distributive Property Chapter Notes | Mathematics for Grade 6 is a part of the Grade 6 Course Mathematics for Grade 6.
All you need of Grade 6 at this link: Grade 6
|
36 videos|76 docs|14 tests
|
FAQs on Distributive Property Chapter Notes - Mathematics for Grade 6
| 1. What is the distributive property in mathematics? |  |
Ans. The distributive property is a fundamental principle in mathematics that states that multiplying a number by a sum is the same as multiplying each addend by the number and then adding the products. It can be expressed as a(b + c) = ab + ac.
| 2. How can the distributive property be used with variables? |  |
Ans. The distributive property can be applied to expressions involving variables in the same way as with numbers. For example, if you have 3(x + 4), you can use the distributive property to rewrite it as 3x + 12, multiplying each term inside the parentheses by 3.
| 3. Can you provide an example of using the distributive property to multiply large numbers? |  |
Ans. Certainly! For instance, to multiply 23 by 5, you can break 23 into 20 + 3. Using the distributive property, you calculate 5(20 + 3) = 5 × 20 + 5 × 3 = 100 + 15 = 115. This method can help simplify calculations with larger numbers.
| 4. Why is the distributive property important in solving equations? |  |
Ans. The distributive property is important in solving equations because it allows for the simplification of expressions, making it easier to isolate variables. By distributing, you can combine like terms and rearrange equations to find solutions more efficiently.
| 5. How can I practice using the distributive property effectively? |  |
Ans. To practice the distributive property, you can work on exercises that involve both numbers and variables. Start with simple problems, then gradually increase the complexity. Additionally, solving real-world problems that require multiplication and addition can enhance your understanding and application of the property.
Related Searches















