Volume and Surface Area Chapter Notes | Mathematics for Grade 6 PDF Download
| Table of contents |

|
| Introduction |

|
| What is surface area? |

|
| Surface area formulas |

|
| Volume of prisms |

|
| Nets |

|
Introduction
Surface area measures the total area of a 3D shape’s faces, while volume measures the space inside it, both using specific formulas for shapes like cubes, prisms, and spheres. Surface area is found by adding the areas of all faces, and volume is often calculated as base area times height. Nets are 2D patterns that fold into 3D shapes, helping visualize and calculate surface area. This guide explains these concepts with simple examples for common 3D shapes.
What is surface area?
- Surface area is the total area of the faces of a three-dimensional shape. Surface area is measured in square units.
- To calculate surface area of a three-dimensional shape, follow these steps:
- Identify all of the two-dimensional faces of the three-dimensional shape.
- Find the area of each face.
- Add the areas together.
Surface area of a cube
Let's try it! Calculate the surface area of the cube.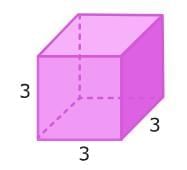 First, identify the shape of each face. You can use nets to help. A cube has six identical square faces.
First, identify the shape of each face. You can use nets to help. A cube has six identical square faces.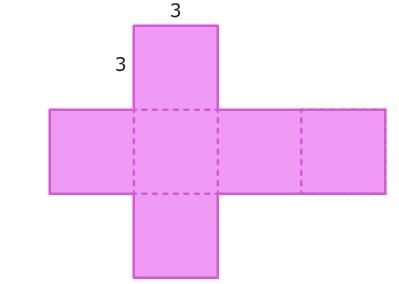 Then, find the area of each face. These faces are squares, so you can multiply the length times the width to find each area.
Then, find the area of each face. These faces are squares, so you can multiply the length times the width to find each area.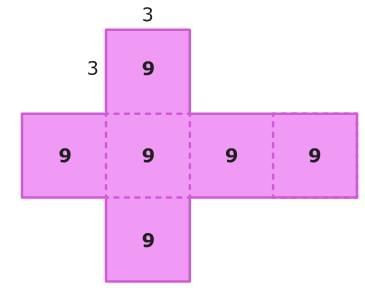
Since 3 x 3 = 9, each square has an area of 9 square units.
Last, add the areas together.
9 + 9 + 9 + 9 + 9 + 9 = 54
So, the surface area of the cube is 54 square units.
Surface area of a rectangular prism
You can use the same steps to calculate the surface area of a rectangular prism. Let's try it.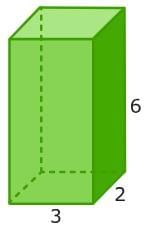 First, identify the shape of each face. A rectangular prism has six rectangular faces that come in pairs.
First, identify the shape of each face. A rectangular prism has six rectangular faces that come in pairs. Then, find the area of each face. These faces are all rectangles, so you can multiply the length times the width to find each area.
Then, find the area of each face. These faces are all rectangles, so you can multiply the length times the width to find each area.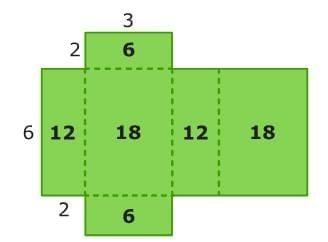
Last, add the areas together.
6 + 6 + 12 + 12 + 18 + 18 = 72
So, the surface area of the rectangular prism is 72 square units.
Surface area of a square pyramid
Follow the steps to find the surface area of a square pyramid. Let's try it.
First, identify the shape of each face. A square pyramid has one square face and four identical triangular faces.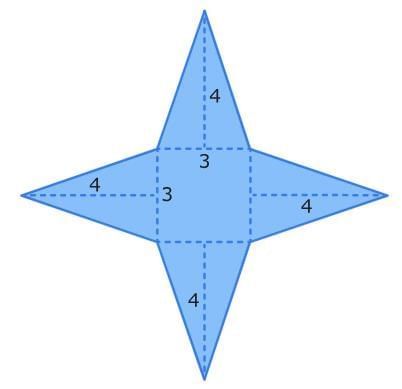
Then, find the area of each face. To find the area of a triangle, multiply 1/2 times the base times the height.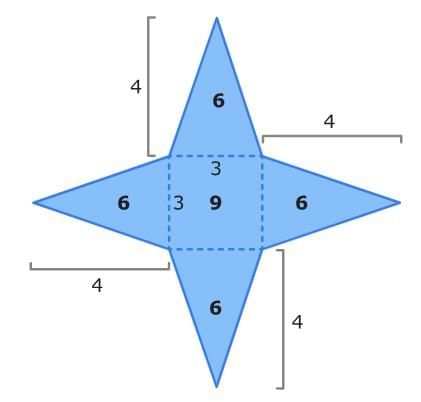
The square has an area of 9 square units. Since 1/2 x 3 x 4 = 6, each triangle has an area of 6 square units.
Last, add the areas together.
9 + 6 + 6 + 6 + 6 = 33
So, the surface area of the square pyramid is 33 square units.
Surface area formulas
Surface area is the combined area of all the faces of a 3D shape and is measured in square units. You can calculate the surface area of 3D figures by using specific formulas. Keep reading to find out more.
What are the surface area formulas?
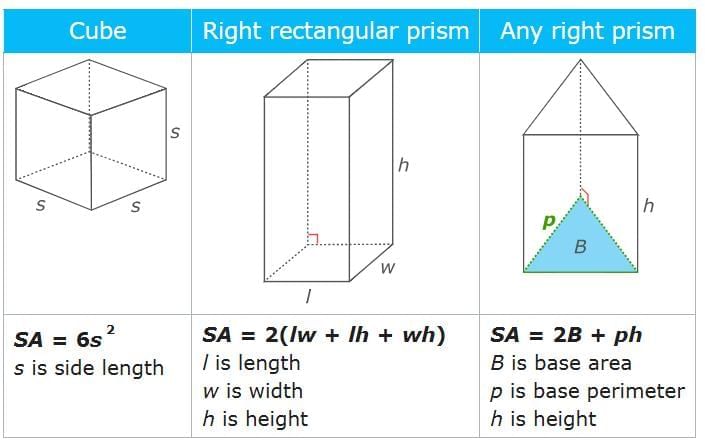
Calculating surface area
Let's find the surface area of some three-dimensional figures:
Cube
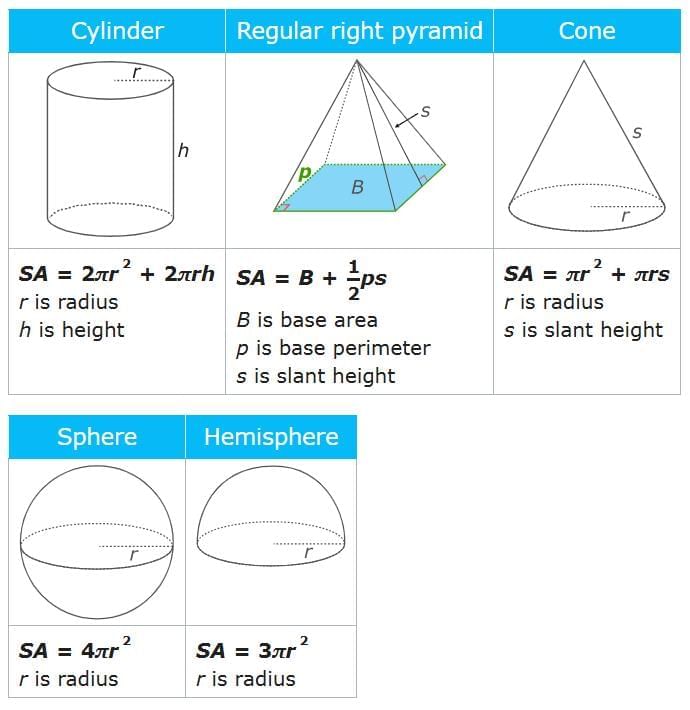
Find the surface area of the cube.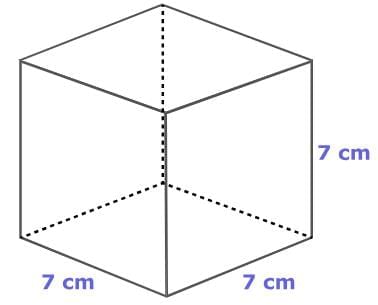 Cubes have six identical square faces. To find the surface area of a cube, calculate the area of one square face and then multiply it by 6.
Cubes have six identical square faces. To find the surface area of a cube, calculate the area of one square face and then multiply it by 6.
SA = 6s2
= 6 x 72
= 6 x 7 x 7
= 6 x 49
= 294
So, the surface area of the cube is 294 square centimeters.
Right rectangular prism
Find the surface area of the rectangular prism.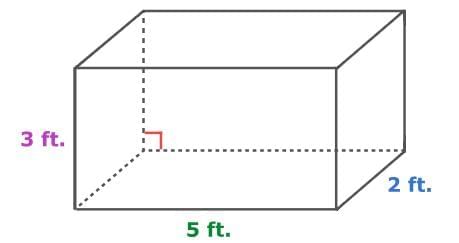
Right rectangular prisms have six faces, made up of three pairs of opposite faces that are the same. To find the surface area, add the areas of one face from each pair, then multiply the total by 2.
SA = 2(lw + lh + wh)
= 2 [(5 x 2) + (5 x 3) + (2 x 3)]
= 2(10 + 15 + 6)
= 2 x 31
= 62
So, the surface area of the prism is 62 square feet.
Right triangular prism
Find the surface area of the triangular prism.
Right prisms have two identical bases connected by rectangular faces. To find their surface area, add the area of the two bases to the area of the rectangular sides.
If the bases are triangles, you can find the area of one triangle by multiplying ½ by the base and height of the triangle. Then, multiply that result by 2 for both bases. To find the area of the rectangular faces, multiply the perimeter of the triangular base by the height of the prism.
SA = 2B + ph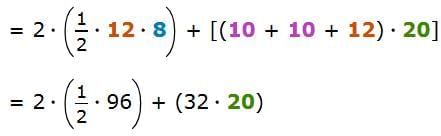
= 248 + 640
= 96 + 640
= 736
So, the surface area of the prism is 736 square inches.
Cylinder
Find the surface area of the cylinder.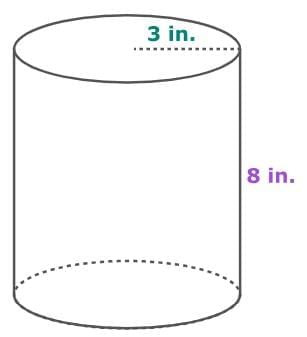
Cylinders have two identical circular bases and one curved surface. To find the surface area of a cylinder, add the area of the circular bases to the area of the curved surface. Start by finding the area of one circular base by multiplying π by the radius squared. Then multiply that result by 2 to get the area of both bases. For the curved surface area, multiply the circumference of the base by the height of the cylinder. The circumference is found by multiplying 2 × π × radius. Use 3.14 as an approximate value for π, and use the symbol ≈ to show "approximately equal to."
SA = 2πr² + 2πrh
= (2π × 3²) + (2π × 3 × 8)
= (2π × 9) + (2π × 24)
= 18π + 48π
= (18 + 48)π
= 66π
≈ 66 × 3.14
≈ 207.24
So, the surface area of the cylinder is approximately 207.24 square inches.
Regular right pyramid
Find the surface area of the pyramid.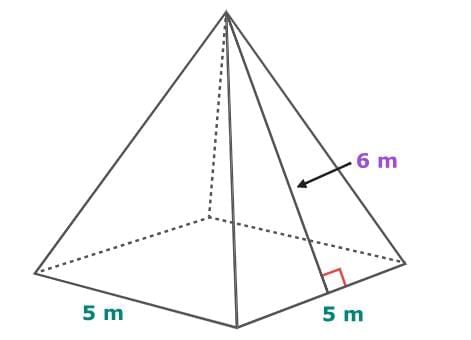
A regular right pyramid has a base and triangular faces that come together at a single point called the vertex. To find its surface area, add the area of the base to the area of the triangular faces. If the base is a square, find its area by multiplying the length by the width. To find the total area of the triangular faces, multiply ½ by the perimeter of the base and the slant height.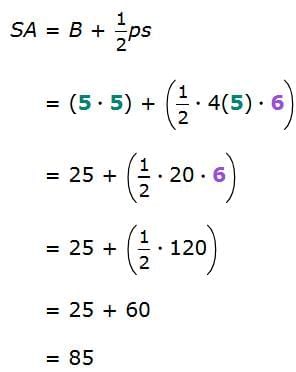
The surface area of the pyramid is 85 square meters.
Cone
Find the surface area of the cone.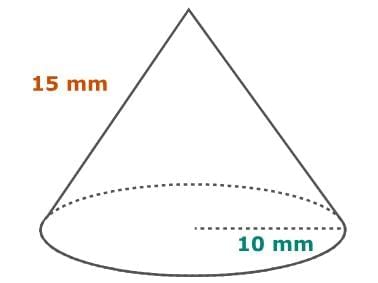 Cones have one circular base and a curved surface. To find the surface area of a cone, add the area of the circular base to the area of the curved surface. To get the area of the base, multiply π by the radius squared. For the curved surface area, multiply π by the radius and the slant height. Use 3.14 as an approximate value for π.
Cones have one circular base and a curved surface. To find the surface area of a cone, add the area of the circular base to the area of the curved surface. To get the area of the base, multiply π by the radius squared. For the curved surface area, multiply π by the radius and the slant height. Use 3.14 as an approximate value for π.
SA = πr² + πrs
= (π × 10²) + (π × 10 × 15)
= (π × 100) + (π × 150)
= π(100 + 150)
= π × 250
≈ 3.14 × 250
≈ 785
So, the surface area of the cone is approximately 785 square millimeters.
Sphere
Find the surface area of the sphere.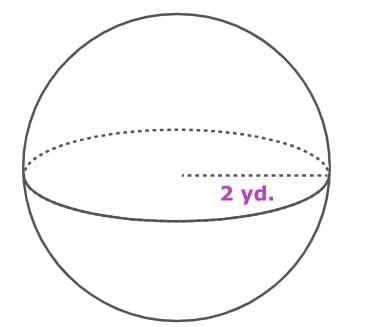
A sphere has a single curved surface. To find its surface area, multiply 4 by π and the square of the radius. Use 3.14 as an approximate value for π.
SA = 4πr²
= 4π × 2²
= 4π × 4
= 16π
≈ 16 × 3.14
≈ 50.24
So, the surface area of the sphere is approximately 50.24 square yards.
Hemisphere
Find the surface area of the hemisphere.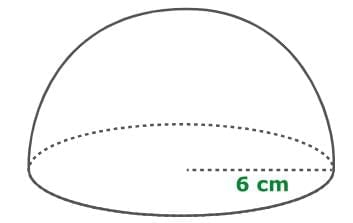
A hemisphere is half of a sphere and has both a curved surface and a flat circular face. To find its surface area, multiply 3 by π and the square of the radius. This comes from adding half the surface area of a full sphere (2πr²) and the area of the circular base (πr²). Use 3.14 as an approximation for π.
SA = 3πr²
= 3π × 6²
= 3π × 36
= 108π
≈ 108 × 3.14
≈ 339.12
So, the surface area of the hemisphere is approximately 339.12 square centimeters.
Volume of prisms
A prism is a three-dimensional figure with flat faces and two identical ends. The two identical ends are called bases. Look at the examples of prisms below:
You can find the volume of a prism by multiplying the area of the base times the height. In the formula below, B is the area of the base and h is height.
V = Bh
Read on to find out how to use this formula to find the volumes of some common three-dimensional figures.
Volume of rectangular prisms
What is volume?
Volume is the amount of space an object takes up. Volume is measured in cubic units. A unit cube has a volume of one cubic unit, or one unit cubed. You can write units cubed as units3.
For Example: Look at the rectangular prism below: The figure is made up of 6 unit cubes.
The figure is made up of 6 unit cubes.
So, the figure has a volume of 6 cubic units or 6 units3.
Formula for volume of a rectangular prism
The formula for the volume of a rectangular prism is length times width times height.
Volume = l × w × h
For Example: The length of this rectangular prism is 4 units. The width of this rectangular prism is 3 units. The height of this rectangular prism is 2 units.
V = 4 × 3 × 2
V = 12 × 2
V = 24
So, the volume of the rectangular prism is 24 cubic units or 24 units3.
Why does this work?
To understand why the formula for the volume of a rectangular prism works, think about layers of cubes.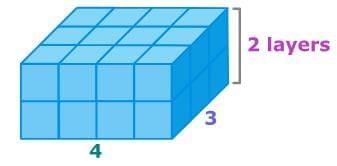
First, multiply the length times the width to find the number of cubes in the bottom layer.
4 × 3 = 12
Now, multiply the number of cubes in one layer by the number of layers to find the total number of cubes in the rectangular prism.
12 × 2 = 24
There are 24 unit cubes, so the volume is 24 cubic units or 24 units3.
Volume of a cube
Find the volume of the cube.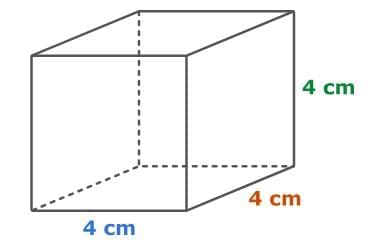 Cubes have square bases. To find the area of the base, multiply the length by the width. Then, to find the volume of the cube, multiply the base area by the height.
Cubes have square bases. To find the area of the base, multiply the length by the width. Then, to find the volume of the cube, multiply the base area by the height.
V = Bh
= (4 × 4) × 4
= 16 × 4
= 64
So, the volume of the cube is 64 cubic centimeters.
Volume of a triangular prism
Find the volume of the triangular prism.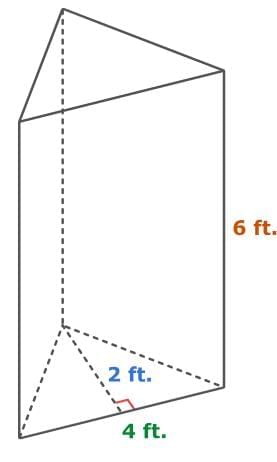
The prism has triangular bases. To find the area of one triangular base, multiply ½ by the base of the triangle and its height. Then, to find the volume of the prism, multiply that base area by the height (or length) of the prism.
V = Bh
= ½ × 4 × 2 × 6
= 4 × 6
= 24
So, the volume of the triangular prism is 24 cubic feet.
Nets
What is a net?
A net is a two-dimensional pattern that can be folded to make a three-dimensional shape.
Nets of common shapes
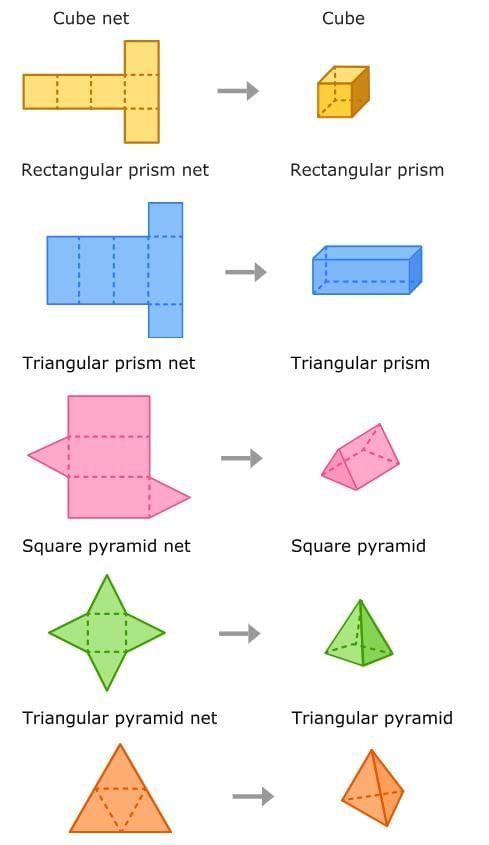 Each three-dimensional shape has multiple nets. A cube, for example, can be made from any of these eleven nets.
Each three-dimensional shape has multiple nets. A cube, for example, can be made from any of these eleven nets.
Nets and surface area
Nets display all the faces of a 3D shape laid out flat. This makes it easy to find the surface area. Simply calculate the area of each face in the net and then add them all together.
Let's try it! Find the surface area of the triangular prism below: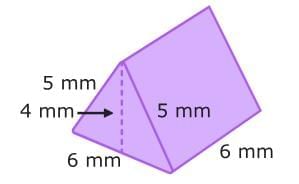 First, create the net of the triangular prism.
First, create the net of the triangular prism.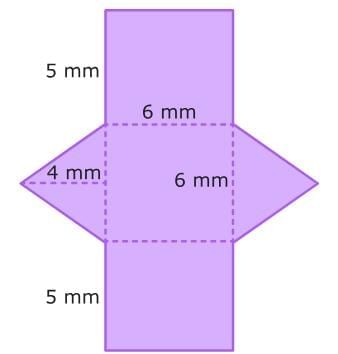 Next, calculate the area of each shape in the net. For rectangles, multiply the length by the width. For triangles, multiply ½ by the base and the height.
Next, calculate the area of each shape in the net. For rectangles, multiply the length by the width. For triangles, multiply ½ by the base and the height.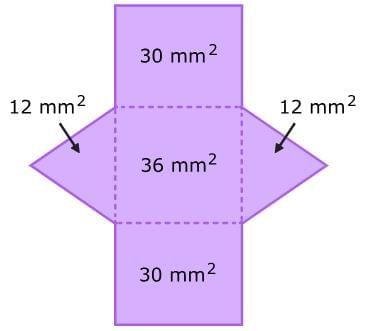
Last, add the areas together.
12 + 12 + 30 + 30 + 36 = 120
So, the surface area of the triangular prism is 120 square millimeters!
|
36 videos|63 docs|14 tests
|
FAQs on Volume and Surface Area Chapter Notes - Mathematics for Grade 6
| 1. What is surface area, and why is it important in geometry? |  |
| 2. What are the common formulas used to calculate the surface area of geometric shapes? |  |
| 3. How do you calculate the volume of prisms, and what is the formula? |  |
| 4. What are nets in geometry, and how do they relate to surface area? |  |
| 5. Can surface area and volume formulas change based on dimensions? |  |



















