GMAT Exam > GMAT Notes > Data Insights for GMAT > Sample Previous Year Questions: Data Sufficiency
Sample Previous Year Questions: Data Sufficiency | Data Insights for GMAT PDF Download
Q1. If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?
1. m > a
2. a + b + c + d = 0
A. Statement (1) ALONE is sufficient, but statement (2) is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) is not sufficient.
C. EACH statement ALONE is sufficient.
D. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
Sol:
Evaluating Statement (1) ALONE: m > a
If a = b = c = d, the average m will be the same as a.
Since m > a, all the elements in the set cannot be the same, and therefore, s > 0.Statement 1 ALONE is sufficient.
Eliminate choices B, C and E. Choices narrow down to A or D.
Evaluating Statement (2) ALONE: a + b + c + d = 0Example: When a = b = c = d = 0, s = 0
Counter Example: When a = -4, b = 0, c = 0, and d = 4, s > 0Statement 2 ALONE is NOT sufficient.
Eliminate choice D.Statement 1 ALONE is sufficient. Choice A is the answer.
Q2. Is x³ > x²?
1. x > 0
2. x < 1
A. Statement (1) ALONE is sufficient, but statement (2) is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) is not sufficient.
C. EACH statement ALONE is sufficient.
D. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
Sol:
Evaluate Statement (1) ALONE
Statement 1: x > 0We know that x is a positive number.
Interval 1: If 0 < x < 1, then x³ < x²
For example, (0.5)³ = 0.125, which is lesser than (0.5)² = 0.25
The answer to the question is NO.Interval 2: If x > 1, then x³ > x²
For example, 2³ = 8 which is greater than 2² = 4
The answer to the question is YES.We do NOT have a DEFINITE answer using statement 1.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C, or E.Evaluate Statement (2) ALONE
Statement 2: x < 1Interval 1: For positive values of x, i.e., 0 < x < 1, we know x³ < x²
The answer to the question is NO.Interval 2: For negative values of x, x³ will be a negative number and x² will be a positive number.
Hence, x³ < x²
The answer to the question is NO.Lastly, what is the answer if x = 0?
When x = 0, x³ = x²
The answer to the question is NO.Hence, if we know that x < 1, we can conclude that x³ is NOT GREATER THAN x².
We have a DEFINITE answer, even if it is NO.Statement 2 ALONE is sufficient. Eliminate choices C and E.
Choice B is the answer.
Q3. If x and y are positive integers, is y odd?
1. x is odd.
2. xy is odd.
A. Statement (1) ALONE is sufficient, but statement (2) is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) is not sufficient.
C. EACH statement ALONE is sufficient.
D. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
Sol:
Evaluate Statement (1) ALONEStatement (1): x is odd.
The statement provides no information about y.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C or E.
Evaluate Statement (2) ALONE
Statement (2): xy is odd.
Given that x and y are integers and that the product xy is odd, both x and y have to be odd (product of two odd integers is odd).
We can answer the question with a definite YES.
Eliminate choices C and E.
Statement 2 ALONE is sufficient. Choice B is the answer.
Q4. Is IaI > a?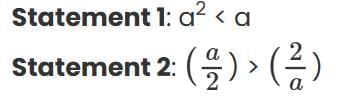
A. Statement (1) ALONE is sufficient, but statement (2) is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) is not sufficient.
C. EACH statement ALONE is sufficient.
D. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
Sol:
Statement 1: a² < aThis inequality holds good only when 0 < a < 1.
i.e., we can conclude that a is positive.
Hence, we can answer the question, “whether ‘a’ is negative” with a definite NO.
Statement 1 ALONE is sufficient.
Eliminate choices B, C, and E. Choices narrow down to A or D.Step 3: Evaluate Statement 2 ALONE
Statement 2: (a/2) > (2/a)
‘a’ is an unknown and can therefore, take both positive and negative values.
We have to evaluate two possibilities from the information given in statement (2).Possibility 1: a > 0
If a > 0, then (a/2) > (2/a) => a² > 4
i.e., a² - 4 > 0 and a > 0
or (a + 2)(a - 2) > 0 and a > 0Rule: If (x - a)(x - b) > 0, x will not lie between ‘a’ and ‘b’.
So, ‘a’ will not lie between -2 and 2. i.e., {a > 2 or a < -2} and a > 0In possibility 1, only positive values of ‘a’ are possible.
∴ the values of ‘a’ that will satisfy the inequality are a > 0 and a > 2
a > 0 and a > 2 implies that a > 2
Possibility 1 therefore, answers the question with a NO.Possibility 2: a < 0
If a < 0, then (a/2) > (2/a) => a² < 4 (the sign of the inequality changes when multiplied with a negative number on both sides)
i.e., a² - 4 < 0 and a < 0
or (a + 2)(a - 2) < 0 and a < 0Rule: If (x - a)(x - b) < 0, x will lie between ‘a’ and ‘b’.
or -2 < a < 2 and a < 0In possibility 2, only negative values of ‘a’ are possible
∴ the range of values that ‘a’ can take narrows down to -2 < a < 0Statement (2) leaves us with both the possibilities: ‘a’ could be positive or ‘a’ could be negative.
We are not able to find a conclusive answer to the question using statement 2.
Statement 2 alone is NOT sufficient.
Eliminate answer option D.
Q5. How many of the numbers x, y, and z are positive if each of these numbers is less than 10?
1. x + y + z = 20
2. x + y = 14
A. Statement (1) ALONE is sufficient, but statement (2) is not sufficient.
B. Statement (2) ALONE is sufficient, but statement (1) is not sufficient.
C. EACH statement ALONE is sufficient.
D. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
E. Statements (1) and (2) TOGETHER are not sufficient.
Sol:
Evaluate Statement (1) ALONE: x + y + z = 20From the question stem we know that each number is less than 10.
So, x < 10, y < 10 and z < 10.
Therefore, the maximum sum of any two of these numbers, say x + y < 20.However, statement 1 states x + y + z = 20.
Unless the third number, z in this case, is also positive x + y + z cannot be 20.
Hence, we can conclude that all 3 numbers x, y and z are positive.Statement 1 ALONE is sufficient.
Eliminate choices B, C, and E. Choices narrow down to A or D.Evaluate Statement (2) ALONE: x + y = 14
As each of x and y is less than 10, both x and y have to be positive for the sum to be 14.
However, z could also be positive or z could be negative.So, there could be either 2 or 3 positive numbers among the three numbers.
We are not able to find a unique answer from the information in statement 2.Statement 2 ALONE is NOT sufficient.
Eliminate choice D.Statement 1 ALONE is sufficient. Choice A is the answer.
Q6. When a positive integer x is divided by a divisor d, the remainder is 24. What is d?
1 . When 2x is divided by d, the remainder is 23.
2. When 3x is divided by d, the remainder is 22.
Sol:
Evaluate Statement (1) ALONE: When 2x is divided by d, the remainder is 23.The question stem tells us that when x is divided by d, the remainder is 24. So if you double x, you’d expect 2 × 24 = 48 as the “would-be” remainder when 2x is divided by d—except statement (1) says the remainder is actually 23. From that we know:
1. d < 48
2. d ≥ 25 (since remainder 24 on x÷d means d > 24)
3. 48 divided by d leaves remainder 23
In equation form: 48 = n·d + 23 ⇒ n·d = 25 ⇒ possible d values are 1, 5, or 25. But since d ≥ 25, only d = 25 works.
Therefore statement (1) alone identifies d uniquely. Statement (1) ALONE is sufficient.
Evaluate Statement (2) ALONE: When 3x is divided by d, the remainder is 22.
If x leaves remainder 24 on division by d, then 3x would “normally” leave remainder 3×24 = 72. But statement (2) says the actual remainder is 22. Therefore:
1. d < 72
2. 72 divided by d leaves remainder 22
So 72 = n·d + 22 ⇒ n·d = 50 ⇒ possible d values are 1, 2, 5, 10, 25, or 50. But from the stem we know d > 24, so only 25 or 50 remain. That’s two possibilities, so we can’t pin down d.
Statement (2) ALONE is not sufficient.
Conclusion: Statement (1) alone suffices; statement (2) does not
Q7. Is the two-digit positive integer P a prime number?
1. (P + 2) and (P – 2) are prime.
2. (P – 4) and (P + 4) are prime.
Sol:
Evaluate Statement (1) ALONE: (P + 2) and (P – 2) are prime.Inference: (P – 2), P and (P + 2) are three consecutive odd integers.
Why?
• Both (P – 2) and (P + 2) are prime, so they must be odd.
• These three numbers differ by 2, so they form an arithmetic sequence of odd integers.
• Among any three consecutive odd integers, one is a multiple of 3.
• If (P – 2) and (P + 2) are prime (i.e. not divisible by 3), the middle number P must be the one divisible by 3.
• A two-digit multiple of 3 cannot be prime.
• The only exception would be the sequence 3, 5, 7—but P must be two-digit, so that case is excluded.Conclusion: Statement (1) alone is sufficient to answer the question.
Evaluate Statement (2) ALONE: (P – 4) and (P + 4) are prime.
Why this works:
For any integer N, the remainders of N – 1, N, and N + 1 on division by 3 are the same cycle: r, r + 1, r + 2 (mod 3).
If (P – 4) is prime, it is not divisible by 3, so its remainder on division by 3 is either 1 or 2. The same remainder applies to (P – 1).
Likewise, if (P + 4) is prime, it too leaves remainder 1 or 2 mod 3, which is the same remainder that P + 1 would leave.
Thus neither (P – 1) nor (P + 1) is divisible by 3.
Among three consecutive integers (P – 1), P, and (P + 1), exactly one must be a multiple of 3. Since the neighbors are not, P itself must be divisible by 3.
P cannot be 3 (it’s two-digit), so it must be a larger multiple of 3 and therefore not prime.
Conclusion: Statement (2) alone is sufficient to answer the question.
Final Answer: Each statement alone suffices. Choice D.
The document Sample Previous Year Questions: Data Sufficiency | Data Insights for GMAT is a part of the GMAT Course Data Insights for GMAT.
All you need of GMAT at this link: GMAT
|
24 videos|28 docs|21 tests
|
FAQs on Sample Previous Year Questions: Data Sufficiency - Data Insights for GMAT
| 1. What is data sufficiency in the context of the GMAT exam? |  |
Ans. Data sufficiency is a specific question type on the GMAT that tests a candidate's ability to determine whether the information provided in the question and the statements can adequately answer the question posed. It assesses analytical reasoning and critical thinking skills, requiring test-takers to evaluate the relevance and sufficiency of data rather than perform extensive calculations.
| 2. How should one approach solving data sufficiency questions on the GMAT? |  |
Ans. To solve data sufficiency questions, candidates should first read the question carefully to understand what is being asked. Then, they should evaluate each statement provided independently to see if it can answer the question. After analyzing the statements, candidates must consider how the statements might work together, if at all, to provide enough information to arrive at a definitive answer.
| 3. What are the answer choices for data sufficiency questions on the GMAT? |  |
Ans. The answer choices for data sufficiency questions are standardized and include:
1) Statement (1) alone is sufficient, but statement (2) alone is not sufficient.
2) Statement (2) alone is sufficient, but statement (1) alone is not sufficient.
3) Both statements together are sufficient, but neither statement alone is sufficient.
4) Each statement alone is sufficient.
5) Statements (1) and (2) together are not sufficient.
| 4. Are there any common pitfalls to avoid when answering data sufficiency questions? |  |
Ans. Yes, common pitfalls include jumping to conclusions without thoroughly analyzing each statement, misinterpreting the question, and overlooking the need to assess statements independently before considering them together. Additionally, candidates should avoid making assumptions beyond the information provided in the statements.
| 5. How can one improve their skills in solving data sufficiency questions for the GMAT? |  |
Ans. To improve skills in solving data sufficiency questions, candidates can practice with a variety of sample questions, review explanations for both correct and incorrect answers, and familiarize themselves with common question types and strategies. Additionally, taking timed practice tests can help build familiarity with the format and improve time management during the actual exam.
Related Searches




















