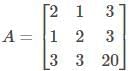Lecture 8 - Eigenvalues and EigenVectors | Algebra- Engineering Maths - Engineering Mathematics PDF Download
| Table of contents |

|
| Eigenvalue Definition |

|
| What are EigenVectors? |

|
| Eigenvalues of a Square Matrix |

|
| Properties of Eigenvalues |

|
| Eigenvalues of 2 x 2 Matrix |

|

Eigenvalue Definition
- Eigenvalues are the special set of scalars associated with the system of linear equations. It is mostly used in matrix equations.
- ‘Eigen’ is a German word that means ‘proper’ or ‘characteristic’.
- Therefore, the term eigenvalue can be termed as characteristic value, characteristic root, proper values or latent roots as well. In simple words, the eigenvalue is a scalar that is used to transform the eigenvector. The basic equation is Ax = λx.
The number or scalar value “λ” is an eigenvalue of A. - In Mathematics, an eigenvector corresponds to the real non zero eigenvalues which point in the direction stretched by the transformation whereas eigenvalue is considered as a factor by which it is stretched. In case, if the eigenvalue is negative, the direction of the transformation is negative.
For every real matrix, there is an eigenvalue. Sometimes it might be complex. The existence of the eigenvalue for the complex matrices is equal to the fundamental theorem of algebra.
What are EigenVectors?
- Eigenvectors are the vectors (non-zero) that do not change the direction when any linear transformation is applied. It changes by only a scalar factor. In a brief, we can say, if A is a linear transformation from a vector space V and x is a vector in V, which is not a zero vector, then v is an eigenvector of A if A(X) is a scalar multiple of x.
- An Eigenspace of vector x consists of a set of all eigenvectors with the equivalent eigenvalue collectively with the zero vector. Though, the zero vector is not an eigenvector.
- Let us say A is an “n × n” matrix and λ is an eigenvalue of matrix A, then x, a non-zero vector, is called as eigenvector if it satisfies the given below expression;
Ax = λx
x is an eigenvector of A corresponding to eigenvalue, λ. - Note:
There could be infinitely many Eigenvectors, corresponding to one eigenvalue.
For distinct eigenvalues, the eigenvectors are linearly dependent.
Eigenvalues of a Square Matrix
- Suppose, An×n is a square matrix, then [A- λI] is called an Eigen or characteristic matrix, which is an indefinite or undefined scalar. Where determinant of Eigen matrix can be written as, |A- λI| and |A- λI| = 0 is the Eigen equation or characteristics equation, where “I” is the identity matrix.
- The roots of an Eigen matrix are called Eigen roots.
- Eigenvalues of a triangular matrix and diagonal matrix are equivalent to the elements on the principal diagonals.
But eigenvalues of the scalar matrix are the scalar only.
Properties of Eigenvalues
- Eigenvectors with Distinct Eigenvalues are Linearly Independent
- Singular Matrices have Zero Eigenvalues
- If A is a square matrix, then λ = 0 is not an eigenvalue of A
- For a scalar multiple of a matrix: If A is a square matrix and λ is an eigenvalue of A. Then, aλ is an eigenvalue of aA.
- For Matrix powers: If A is square matrix and λ is an eigenvalue of A and n ≥ 0 is an integer, then λn is an eigenvalue of An.
- For polynomials of matrix: If A is a square matrix, λ is an eigenvalue of A and p(x) is a polynomial in variable x, then p(λ) is the eigenvalue of matrix p(A).
- Inverse Matrix: If A is a square matrix, λ is an eigenvalue of A, then λ-1 is an eigenvalue of A-1
- Transpose matrix: If A is a square matrix, λ is an eigenvalue of A, then λ is an eigenvalue of At
EigenValue Example
In this shear mapping, the blue arrow changes direction, whereas the pink arrow does not. Here, the pink arrow is an eigenvector because it does not change direction. Also, the length of this arrow is not changed; its eigenvalue is 1.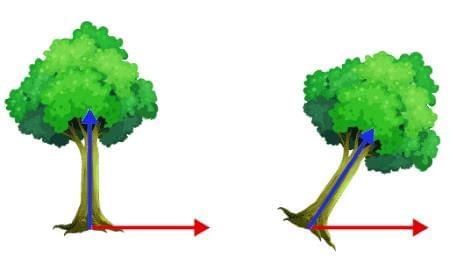
Eigenvalues of 2 x 2 Matrix
Let us have a look at the example given below to learn how to find the eigenvalues of a 2 x 2 matrix.
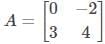
Solution:
Given,
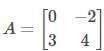 Using the characteristic equation,
Using the characteristic equation,Let
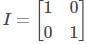 be the 2 x 2 identity matrix.
be the 2 x 2 identity matrix.|A – λI| = 0
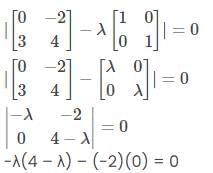 -4λ + λ2 = 0
-4λ + λ2 = 0λ(λ – 4) = 0
λ = 0 or λ – 4 = 0
Thus, λ = 0 or λ = 4
Hence, the two eigenvalues of the given matrix are λ = 0 and λ = 4.
Go through the following problem to find the Eigenvalue of 3 x 3 matrix.
Example: Find the Eigenvalue for the matrix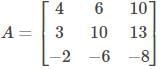
Sol:
Given Matrix: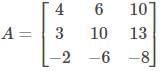
To find: Eigenvalues, λi
We know that λi are the roots of det (A-λI)
Where, “I” is the identity Matrix.
Therefore,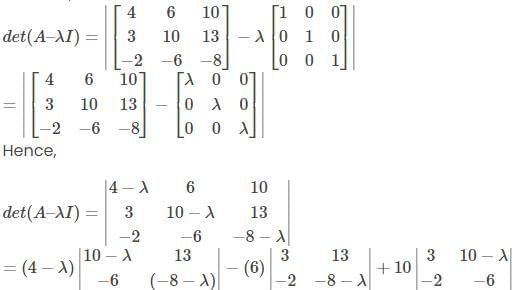 = (4 − λ) [(10 − λ) (− 8 − λ) − 13 (− 6)] − 6 [(3) (− 8 − λ) − 13 (− 2)] + 10 [(3) (−6) − (10 − λ) (− 2)]
= (4 − λ) [(10 − λ) (− 8 − λ) − 13 (− 6)] − 6 [(3) (− 8 − λ) − 13 (− 2)] + 10 [(3) (−6) − (10 − λ) (− 2)]
Now, take the first part from the above equation.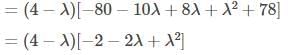
On simplifying the above expression, we get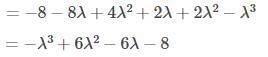 which is the simplified form of the first term of the expression. …(1)
which is the simplified form of the first term of the expression. …(1)
Similarly, for the second term of the equation, we get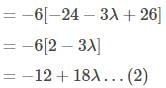 Similarly, for the third term,
Similarly, for the third term,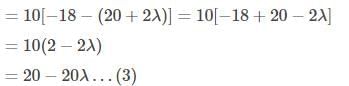
Hence,
det (A-λI) = (1)+(2)+(3)
det (A-λI) = -λ3 + 6λ2 – 6λ – 8 – 12 +18λ +20-20λ
=-λ3+6λ2-8λ+0
Therefore, the Eigenvalues of the matrix A can be found by
-λ3+6λ2-8λ =0
Now, multiply the above equation by (-1) on both sides, we get
λ3-6λ2+8λ =0
On factoring the above equation, we get
λ(λ2-6λ+8)=0
Thus,
λ = 0, and (λ2-6λ + 8) = 0
Use the quadratic equation formula to find the roots of the equation (λ2-6λ + 8) = 0
Here, a = 1, b = -6, c = 8
Now, the values in the quadratic formula,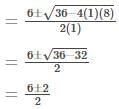
Hence, λ= 2 and λ=4
Therefore, the Eigenvalues of matrix A are 0, 2, 4.
Practice Problems
Find the Eigenvalues for the following Matrices.
FAQs on Lecture 8 - Eigenvalues and EigenVectors - Algebra- Engineering Maths - Engineering Mathematics
| 1. What is the definition of an eigenvalue and how is it related to linear transformations? |  |
| 2. What are eigenvectors and how do they differ from regular vectors? |  |
| 3. What are some important properties of eigenvalues? |  |
| 4. How can we find the eigenvalues of a 2 x 2 matrix? |  |
| 5. Why are eigenvalues and eigenvectors significant in engineering mathematics? |  |