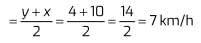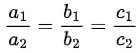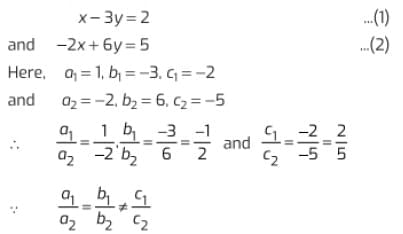Assignment: Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download
Multiple Choice Questions
Q1. The pairs of equations x + 2y-5 = 0 and -4x - 8y + 20 = 0 have:
(a) Unique solution
(b) Exactly two solutions
(c) Infinitely many solutions
(d) No solution
Ans. (c) Infinitely many solutions
a1/a2 = 1/-4
b1/b2 = 2/-8 = 1/-4
c1/c2 = -5/20 = -1/4
This shows:
a1/a2 = b1/b2 = c1/c2
Therefore, the pair of equations has infinitely many solutions.
Q2. If a pair of linear equations is consistent, then the lines are:
(a) Parallel
(b) Always coincident
(c) Always intersecting
(d) Intersecting or coincident
Ans. (d) Intersecting or coincident
Because the two lines definitely have a solution.
Q3. The pairs of equations 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0 have
(a) Unique solution
(b) Exactly two solutions
(c) Infinitely many solutions
(d) No solution
Ans. (d) No solution
Given, 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2
c1/c2 = 12/26 = 6/13
Since, a1/a2 = b1/b2 ≠ c1/c2
So, the pairs of equations are parallel and the lines never intersect each other at any point, therefore there is no possible solution.
Q4. If the lines 3x + 2ky – 2 = 0 and 2x + 5y + 1 = 0 are parallel, then what is the value of k?
(a) 4/15
(b) 15/4
(c) 4/5
(d) 5/4
Ans. (b) 15/4
The condition for parallel lines is:
a1/a2 = b1/b2 ≠ c1/c2
Hence, 3/2 = 2k/5
k=15/4
Q5. If one equation of a pair of dependent linear equations is -3x+5y-2=0. The second equation will be:
(a) -6x + 10y - 4 = 0
(b) 6x - 10y - 4 = 0
(c) 6x + 10y - 4 = 0
(d) -6x + 10y + 4 = 0
Ans. (a) -6x+10y-4=0
The condition for dependent linear equations is:
a1/a2 = b1/b2 = c1/c2
For option a,
a1/a2 = b1/b2 = c1/c2= ½
Short and Long Questions
Q1. The sum of the digits of a two digit number is 8 and the difference between the number and that formed by reversing the digits is 18. Find the number.
Let unit and tens digit be x and y.
∴ Original number = 1x + 10y …(i)
Reversed number = 10x + 1y
According to question,
x + y = 8
⇒ y = 8 – x …(ii)
Also, 1x + 10Oy – (10x + y) = 18
⇒ x + 10y – 10x – y = 18
⇒ 9y – 9x = 18
⇒ y – x = 2 …[Dividing both sides by 9
⇒ 8 – x – x = 2 …[From (it)
⇒ 8 – 2 = 2x
⇒ 2x = 6
From (it), y = 8 – 3 = 5
From (i), Original number = 3 + 10(5) = 53
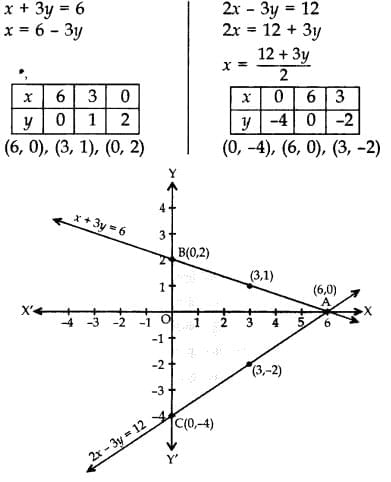
Q2. Solve the following pair of linear equations graphically:
x + 3y = 6 ; 2x – 3y = 12
Also find the area of the triangle formed by the lines representing the given equations with y-axis.
Q3. The age of the father is twice the sum of the ages of his 2 children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Let the present ages of his children be x years and y years.
Then the present age of the father = 2(x + y) …(i)
After 20 years, his children’s ages will be
(x + 20) and (y + 20) years
After 20 years, father’s age will be 2(x + y) + 20
According to the Question,
⇒ 2(x + y) + 20 = x + 20 + y + 20
⇒ 2x + 2y + 20 = x + y + 40
⇒ 2x + 2y – x – y = 40 – 20
⇒ x + y = 20 …[From (i)
∴ Present age of father = 2(20) = 40 years
Q4. On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(i) Given : 3x + 2y = 5 or 3x + 2y – 5 = 0
and 2x – 3y = 7 or 2x – 3y – 7 = 0
Comparing the above equations with a1x + b1y + c1=0
And a2x + b2y + c2 = 0
We get,
a1 = 3, b1 = 2, c1 = -5
a2 = 2, b2 = -3, c2 = -7
a1/a2 = 3/2,
b1/b2 = 2/-3,
c1/c2 = -5/-7 = 5/7
Since, a1/a2 ≠ b1/b2 the lines intersect each other at a point and have only one possible solution.
Hence, the equations are consistent.(ii) Given 2x – 3y = 8 and 4x – 6y = 9
Therefore,
a1 = 2, b1 = -3, c1 = -8
a2 = 4, b2 = -6, c2 = -9
a1/a2 = 2/4 = 1/2,
b1/b2 = -3/-6 = 1/2,
c1/c2 = -8/-9 = 8/9
Since, a1/a2 = b1/b2 ≠ c1/c2
Q5. Solve by elimination:
3x = y + 5
5x – y = 11
We have, 3x = y + 5, and 5x – y = 11
Putting the value of x in (i), we get
3x – y = 5 ⇒ 3(3) – y = 5
9 – 5 = y ⇒ y = 4
∴ x = 3, y = 4
Case Based Questions
Sanjeev a student of class X, goes to Yamuna river with his friends. When he saw a boat in the river, then he wants to sit in boat. So his all friends are ready to sit with him. In this order, Sanjeev is sitting on a boat which upstream at a speed of 8 km/h and downstream at a speed of 16 km/h. When Sanjeev is in the boat, some questions are arises in the mind, then answer the given questions.  Based on the above information, solve the following questions:
Based on the above information, solve the following questions:
Q1. The speed of the boat in still water is:
(a) 8 km/h
(b) 10 km/h
(c) 12 km/h
(d) 14 km/h
Ans. (b)
Let the speed of the boat in still water be x km/h and speed of the stream be y km/h.
Then, x - y = 6 ...(1)
x + y = 14 ...(2)
On adding eqs. (1) and (2), we get
2x = 20 = x = 10
.. Speed of the boat in still water is 10 km/h
So, option (b) is correct.
Q2. The speed of the stream is:
(a) 3 km/h
(b) 4 km/h
(c) 6 km/h
(d) 5 km/h
Ans. (b)
On putting the value of x in eq. (2), we get
10 + y = 14
= y = 14 - 10 = 4
.. Speed of the stream is 4 km/h.
So, option (b) is correct.
Q3. Which mathematical concept is used in the above problem?
(a) Pair of linear equations
(b) Cross-multiplication method
(c) Factorisation method
(d) None of the above
Ans. (a)
Pair of linear equation concept is used in above problem.
So, option (a) is correct.
Q4. The direction in which the speed is maximum is:
(a) Upstream
(b) Downstream
(c) Both have equal speed
(d) None of the above
Ans. (b)
In downstream, the speed is maximum because in downstream, the speed is (x + y) km/h and in upstream, the speed is (x - y) km/h. So, option (b) is correct.
Q5. The average speed of stream and boat in still water is:
(a) 7 km/h
(b) 10 km/h
(c) 12 km/h
(d) 5 km/h
Ans. (a)
Average speed of stream and boat in still water
So, option (a) is correct
The resident welfare association of a Radheshyam society decided to build two straight paths in their neighbourhood park such that they do not cross each other and also plant trees along the boundary lines of each path. 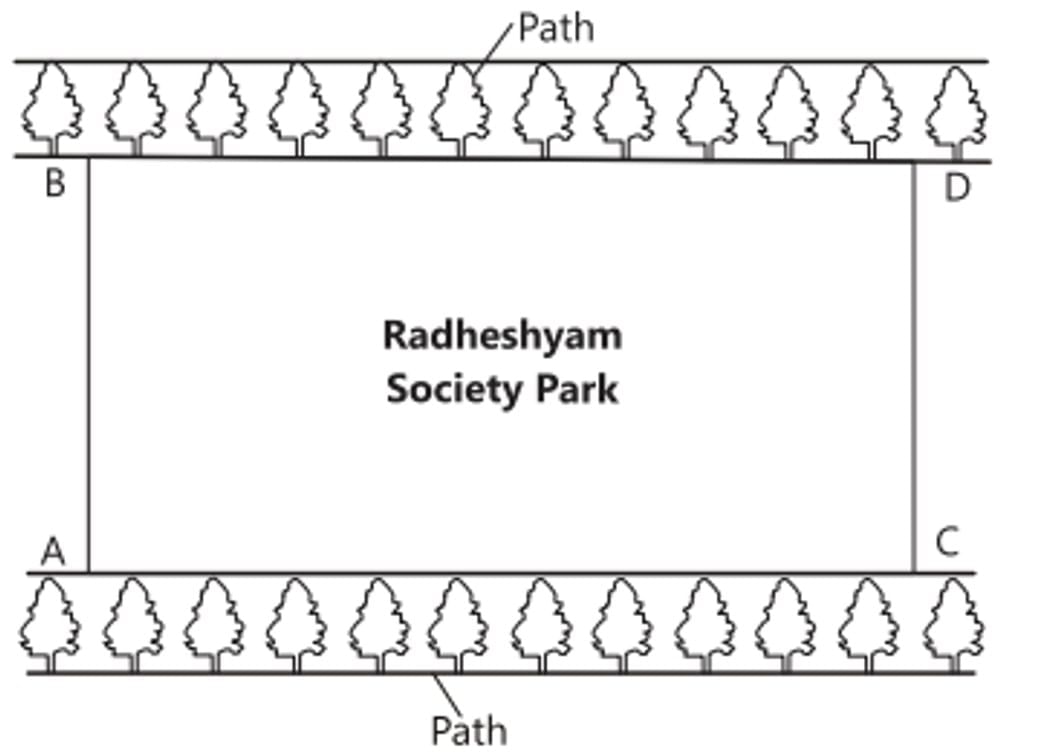
One of the members of association Shyam Lal suggested that the paths should be constructed represented by the two linear equations x-3y = 2 and -2x + 6y = 5.
Based on the above information, solve the following questions:
Q1. If the pair of equations ax + b1y + c1 = 0 and a2x + b2y + c2 = 0 has infinitely solutions, then condition is:
(a) 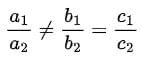
(b) 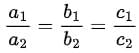
(c) 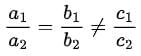
(d) None of these
Ans. (b)
If the pair of equation ax + by + G1 = 0 and a2x + b2y + c2 = 0 has infinitely solutions, then condition is
So, option (b) is correct
Q2. If pair of lines are parallel, then pair of linear equations is:
(a) inconsistent
(b) consistent
(c) consistent or inconsistent
(d) None of the above
Ans. (b)
If pair of lines are parallel, then pair of linear equation is consistent. So, option (b) is correct.
Q3. Check whether the two paths will cross each other or not.
(a) Yes
(b) No
(c) Can't say
(d) None of these
Ans. (b)
Given, equation of paths are
So, the paths represented by the equations are parallel i.e., do not intersect each other. So, option (b) is correct.
Q4. How many point(s) lie on the line x − 3y = 2?
(a) One
(b) Two
(c) Three
(d) Infinitely
Ans. (d)
Infinitely point lies on the line x-3y=2. So, option (d) is correct.
Q5. If the line 2x + 6y = 5 intersects the X-axis, then find its coordinate.
(a) (−2.5, 0)
(b) (2.5, 0)
(c) (0, 2.5)
(d) (0, −2.5)
Ans. (b)
The y-coordinate on X-axis is zero.
Put y= 0 in 2x + 6y = 5, we get
2x + 6(0) = 5
⇒ x = 5/2 = 2.5
|
127 videos|584 docs|79 tests
|
FAQs on Assignment: Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10
| $1. What are linear equations in two variables, and how are they represented? |  |
| $2. How can we solve a pair of linear equations in two variables? |  |
| $3. What is the significance of the solution of a pair of linear equations? |  |
| $4. Can you explain the graphical representation of linear equations in two variables? |  |
| $5. What are the real-world applications of solving linear equations in two variables? |  |