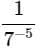Worksheet Solutions: Power Play | Worksheets with Solutions for Class 8 PDF Download
| Table of contents |

|
| 1. Multiple Choice Questions |

|
| 2. State true or false |

|
| 3. Fill in the Blanks |

|
| 6. Answer the following Questions |

|
1. Multiple Choice Questions
Q1: What is the base of the exponent 69?
(a) 6
(b) 2
(c) 9
(d) None
Ans: (a)
The base of the exponent 69 is 6
Q2: Find the missing number
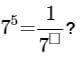
(a) 2
(b) −5
(c) 1
(d) None
Ans: (b)
The missing number should be −5
So the answer will be 75 =
Q3: Find the value of (52)2
(a) 125
(b) 625
(c) 25
(d) 0
Ans: (b)
The solution will be
(52)2=54
(52)2=5×5×5×5
(52)2= 625
Q4: In prime factorization, 3600 can be written as:
(a) 2⁴ × 3² × 5²
(b) 2³ × 3³ × 5²
(c) 2⁴ × 3² × 5³
(d) 2² × 3⁴ × 5²
Answer: (a)
3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
Q5: Find the value of x, when 2x=44
(a) x=6
(b) x=2
(c) x=8
(d) x=−5
Ans: (c)
The solution will be
2x=44
2x=(22)4
2x=28
2x=28
x=8
So the answer will be x=8
Q5: Which rule of exponents is used in the expression (3²)⁴ = 3⁸?
(a) Product Rule
(b) Power of a Power Rule
(c) Quotient Rule
(d) Negative Exponent Rule
Answer: (b)
Q6: Which of the following is the usual form of 5.8 × 10¹²?
(a) 5800000000000
(b) 580000000000
(c) 0.0000000000058
(d) 5.8 × 1000000000
Answer: (a) 5800000000000
Q7: Which of the following is the correct result of 2³ × 5³?
(a) 10³
(b) 7³
(c) 1000
(d) Both (a) and (c)
Answer: (d)
2³ × 5³ = (2 × 5)³ = 10³ = 1000
Q8: If a password can be made using 26 letters and has 4 characters, the total number of possible passwords is:
(a) 264
(b) 426
(c) 26 × 4
(d) 4262
Answer: (a)
26 choices for each of 4 positions.
Q9: The scientific notation of 9540000000000000 is:
(a) 9.54 × 10¹⁵
(b) 95.4 × 10¹⁴
(c) 0.954 × 10¹⁶
(d) 9.54 × 10¹⁴
Answer: (a) 9.54 × 10¹⁵
Q10: Find the value of (211+62−51)0= ?
(a) 0
(b) −1
(c) 1
(d) None
Ans: (c)
The solution will be
(211+62−51)0=(anything)0
(211+62−51)0=1
So the solution will be
(211+62−51)0=1
2. State true or false
Q1: (100+120)(160+120)=82
Ans: False
Sol: (Anything)0 =1 therefore, LHS= 1
RHS= 82 = 64
hence false
Q2: (34)2=38
Ans: True
Sol: LHS = (34)2 = (3)8
RHS = (3)8
Q3: According to the product rule of exponents, 3² × 3⁵ = 3¹⁰.
Ans: False
Sol: It should be 3(2+5) = 37.
Q4: Among 27,32,42, and 63, 63 is the greatest.
Ans: True
Sol: Since we have
27 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
32 = 3 × 3 = 9
42 = 4 × 4 = 16
63 = 6 × 6 × 6 = 216
In this, 63 is greater.
Q5: Linear growth means multiplying by a fixed factor at each step.
Ans: False
Sol: The statement describes exponential growth; linear growth adds a fixed amount.
Q6: The zero exponent rule states that 0ⁿ = 1 for all values of n.
Ans: False
Sol: The zero exponent rule applies only when the base is not zero.
3. Fill in the Blanks
Q1: The power of a power rule states that (nᵃ)ᵇ =________.
Ans: n⁽ᵃ×ᵇ⁾
Q2: Using the quotient rule: 7⁹ ÷ 7⁴ = ________.
Ans: 7⁵
Q3: The negative exponent rule says 3⁻² = _______.
Ans: 1/9
Q4: Prime factorization of 81 in exponential form is _______.
Ans: 3⁴
Q5: A number in scientific notation is written as x × 10ᵃ where 1 ≤ x < _______.
Ans: 10
6. Answer the following Questions
Q1: Follow the pattern and complete
Ans: The pattern for the solution is square root of the numbers which continue as
1234321=11112
123454321=111112
Q2: If 2x × 5x=1000 then x=?
Ans: For solving we will just factorise
2x ×5x=1000
2x × 5x = 5 × 5 × 5 × 2 × 2 × 2
2x × 5x = 23 × 53
x = 3
Q3: Find 33+ 43 + 53 and give the answers in cube
Ans: Solve the expression
33+43+53 = 27+64+125
33+43+53 = 216
33+43+53 = 6×6×6
33+43+53 = 63
Q4: Find the missing number x in 52+x2=132
Ans: Solve the expression
52+x2=132
25+x2=169
x2=144
x=√144
x=12
Q5: Simplify in exponent form (34× 32)÷ 3−4
Ans: Solving the expression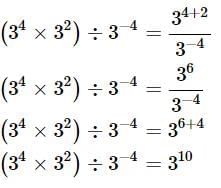
Q6: Expand
(a) 1526.26
(b) 8379
Using exponents
Ans: Solve in exponential form
(a) 1526.26 = 1×103+5×102+2×101+6×100 +2×10−1 + 6×10−2
(b) 8379 = 8×103+3×102+7×101+9×100
Q7: Express the following number as a product of powers of prime factors.
(a) 1225
(b) 3600
Ans: Solve in exponential form
(a) 1225=5×5×7×7
1225=52×72
(b) 3600=2×2×2×2×3×3×5×5
3600=24×32×52
Q8: Express the following large no’s in its scientific notation.
(a) 491200000
(b) 301000000
Ans: Solve in exponential form
(a) 491200000, move the decimal point 8 places to the left: 4.912×108
(b) 9540000000000000, move the decimal point 15 places to the left: 9.54 × 1015
Q9: Express the following in usual form
(a) 3.02 ×10−6
(b) 5.8 × 1012
Ans: (a) 3.02 ×10−6
To convert a smaller number(negative powers of 10) to its usual form shift the decimal towards the left by the number of places equivalent to the power of 10.
3.02 × 10−6 = 3.02/1000000
∴ its usual form is 0.00000302
(b) 5.8 × 1012 = 5800000000000 [Moving the decimal towards the right by 12 places]
∴ its usual form is 5800000000000
Q10: Prove that
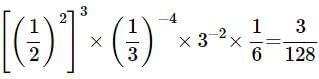
Ans: Solve the left hand side and equate with the right
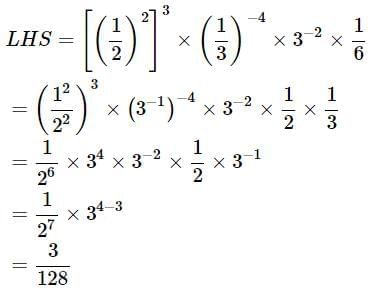
FAQs on Worksheet Solutions: Power Play - Worksheets with Solutions for Class 8
| 1. What is the importance of power play in sports and how does it impact the outcome of a game? |  |
| 2. How can players enhance their skills during a power play situation? |  |
| 3. What are some common strategies used during a power play in team sports? |  |
| 4. What are the rules governing power plays in different sports? |  |
| 5. How can coaches effectively prepare their teams for power play situations? |  |