Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Important Formulas: Quadrilaterals
Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |
|
| 1. Polygons |
|
| 2. Quadrilateral |
|
| 3. Rectangle |
|
| 4. Square |
|
| 5. Parallelogram |
|
| 6. Rhombus |
|
| 7. Kite |
|
| 8. Trapezium |
|
| 9. Venn Diagram Relationships |
|
1. Polygons
A simple closed curve made up of only line segments is called a polygon.
Regular and Irregular Polygons
A regular polygon is both ‘equiangular’ and ‘equilateral’. So all the sides and angles should be same
(a) So square is a regular polygon, but a rectangle is not
(b) Equilateral triangle is a regular polygon
2. Quadrilateral
Definition: A quadrilateral is a four-sided figure, derived from Latin words "quadri" (four) and "latus" (sides). There are many kinds of quadrilaterals. 
The five most common types are the parallelogram, the rectangle, the square, the trapezoid, and the rhombus.
Angle Property of Quadrilateral
- Sum of all the interior angles is 360º
- Sum of all the exterior angles is 360º
3. Rectangle
Definition: A quadrilateral with all angles equal to 90°.
Properties:
All angles are 90°.
Opposite sides are equal.
Opposite sides are parallel.
Diagonals are equal in length and bisect each other (intersect at their midpoints).
4. Square
Definition: A quadrilateral with all angles equal to 90° and all sides of equal length.
Properties:
All sides are equal.
Opposite sides are parallel.
All angles are 90°.
Diagonals are equal, bisect each other at 90°, and bisect the square’s angles (e.g., ∠ADC is split into two 45° angles).
A square is a special type of rectangle and parallelogram.
5. Parallelogram
Definition: A quadrilateral that has both pairs of opposite sides parallel is called a parallelogram.
Properties:
- The opposite sides of a parallelogram are equal.
- The opposite angles of a parallelogram are equal.
- The diagonals of a parallelogram bisect each other.
- The adjacent angles in a parallelogram are supplementary.
6. Rhombus
Definition: A quadrilateral with all sides of equal length.
Properties:
All sides are equal.
Opposite sides are parallel (a rhombus is a parallelogram).
Adjacent angles sum to 180°, and opposite angles are equal.
Diagonals bisect each other at 90° and bisect the rhombus’s angles.
7. Kite
Definition: It is a quadrilaterals having exactly two distinct consecutive pairs of sides of equal length
Here ABCD is a Kite
Properties:
Two pairs of adjacent sides are equal.
AB=BC
AD=CDOne diagonal (e.g., BD) bisects the other (AC) at 90° and bisects opposite angles (∠ABC, ∠ADC).
8. Trapezium
A quadrilateral which has one pair of opposite sides parallel is called a trapezium.
Properties:
At least one pair of opposite sides is parallel.
In an isosceles trapezium (non-parallel sides equal), angles opposite the equal sides are equal, and base angles sum to 180°.
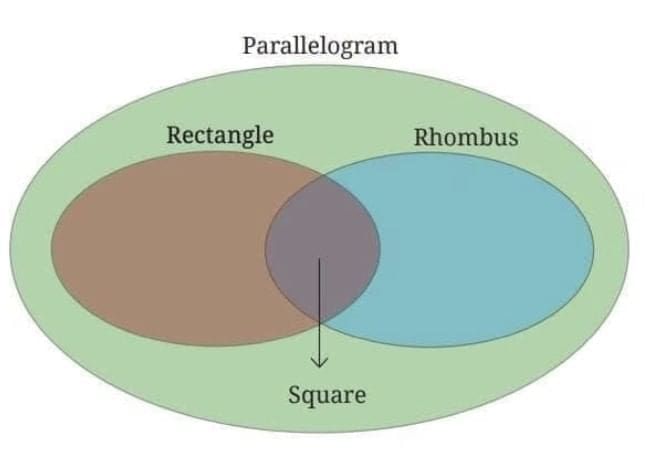
9. Venn Diagram Relationships
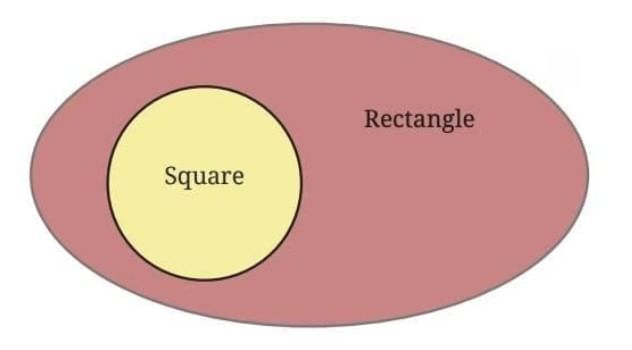
(a) Venn Diagram Showing the Relationship Between a Rectangle and a Square
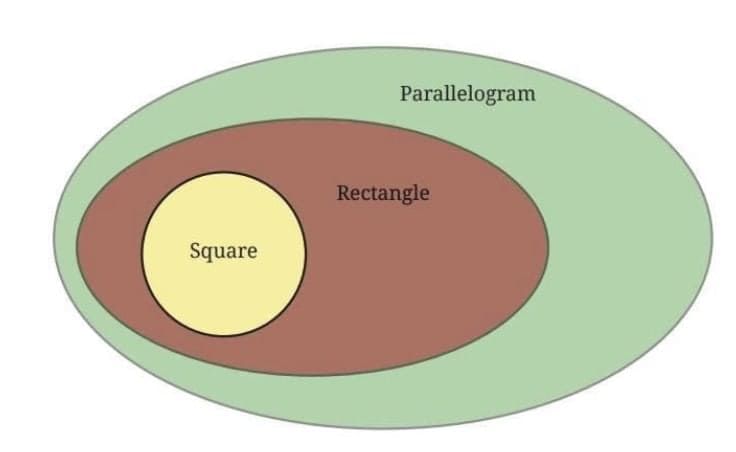
(b) Venn Diagram Showing Relationship Between Square, Rectangle and Parallelogram.
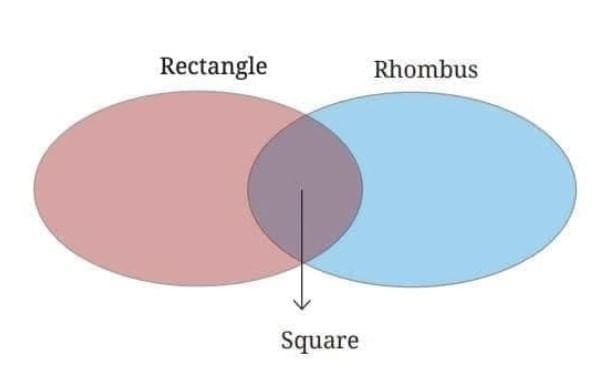
(c) Venn Diagram Showing Relationship Between Rectangle, Rhombus, and Square
(d) Venn Diagram Showing Relationship Between Rectangle, Rhombus, Parallelogram and Square
The document Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
26 videos|133 docs|11 tests
|
FAQs on Important Formulas: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the different types of quadrilaterals and their properties? |  |
Ans. Quadrilaterals are four-sided polygons that can be classified into several types based on their properties. The main types include:
1. <b>Rectangle</b>: Opposite sides are equal, and all angles are 90 degrees.
2. <b>Square</b>: All sides are equal, and all angles are 90 degrees. It is a special type of rectangle.
3. <b>Rhombus</b>: All sides are equal, but angles are not necessarily 90 degrees. Opposite angles are equal, and adjacent angles are supplementary.
4. <b>Trapezium (or Trapezoid)</b>: At least one pair of opposite sides is parallel. The angles adjacent to each base are supplementary.
5. <b>Parallelogram</b>: Opposite sides are equal and parallel. Opposite angles are equal, and adjacent angles are supplementary.
Understanding these properties helps in solving various geometric problems involving quadrilaterals.
| 2. How do you calculate the area of different types of quadrilaterals? | |
Ans. The area of quadrilaterals can be calculated using specific formulas based on their type:
1. <b>Rectangle</b>: Area = length × width.
2. <b>Square</b>: Area = side².
3. <b>Rhombus</b>: Area = (diagonal₁ × diagonal₂) / 2, where diagonal₁ and diagonal₂ are the lengths of the diagonals.
4. <b>Trapezium</b>: Area = (1/2) × (base₁ + base₂) × height, where base₁ and base₂ are the lengths of the parallel sides and height is the perpendicular distance between them.
5. <b>Parallelogram</b>: Area = base × height.
These formulas make it easier to determine the area based on the dimensions provided.
| 3. What is the sum of the interior angles of a quadrilateral? | |
Ans. The sum of the interior angles of any quadrilateral is always 360 degrees. This can be derived from the formula for the sum of interior angles of a polygon, which is (n-2) × 180 degrees, where n is the number of sides. For a quadrilateral, n = 4, so the sum is (4-2) × 180 = 2 × 180 = 360 degrees.
| 4. What are the properties of a parallelogram that distinguish it from other quadrilaterals? | |
Ans. A parallelogram has several unique properties that set it apart from other quadrilaterals:
1. Opposite sides are equal in length and parallel.
2. Opposite angles are equal.
3. Adjacent angles are supplementary (add up to 180 degrees).
4. The diagonals bisect each other at their midpoints.
5. The area can be calculated using the formula: Area = base × height.
These properties are essential for identifying and solving problems related to parallelograms.
| 5. How do you determine if a quadrilateral is a trapezium? | |
Ans. To determine if a quadrilateral is a trapezium, you should check for the following criteria:
1. At least one pair of opposite sides must be parallel. This is the defining characteristic of trapeziums.
2. The other pair of sides can be of any length and may or may not be parallel.
3. If both pairs of opposite sides are parallel, the trapezium is specifically called an isosceles trapezium if the non-parallel sides are equal in length.
By verifying these properties, you can classify a quadrilateral as a trapezium.
About this Document
4.88/5
Rating
Oct 09, 2025
Last updated
Related Exams
Document Description: Important Formulas: Quadrilaterals for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Important Formulas: Quadrilaterals have been prepared according to the Class 8 exam syllabus. Information about Important Formulas: Quadrilaterals covers topics
like 1. Polygons, 2. Quadrilateral, 3. Rectangle, 4. Square, 5. Parallelogram, 6. Rhombus, 7. Kite, 8. Trapezium, 9. Venn Diagram Relationships and Important Formulas: Quadrilaterals Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulas: Quadrilaterals.
Introduction of Important Formulas: Quadrilaterals in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Important Formulas: Quadrilaterals in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Important Formulas: Quadrilaterals
In this doc you can find the meaning of Important Formulas: Quadrilaterals defined & explained in the simplest way possible. Besides explaining types of
Important Formulas: Quadrilaterals theory, EduRev gives you an ample number of questions to practice Important Formulas: Quadrilaterals tests, examples and also practice Class 8
tests
Related Searches
Objective type Questions
,practice quizzes
,past year papers
,Sample Paper
,Semester Notes
,mock tests for examination
,video lectures
,Viva Questions
,Exam
,Free
,Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Previous Year Questions with Solutions
,Important Formulas: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash)
,Extra Questions
,MCQs
,Important questions
,shortcuts and tricks
,Summary
,ppt
,study material
;
Additional Information about Important Formulas: Quadrilaterals for Class 8 Preparation
Important Formulas: Quadrilaterals Free PDF Download
The Important Formulas: Quadrilaterals is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulas: Quadrilaterals now and kickstart your journey towards success in the Class 8 exam.
Importance of Important Formulas: Quadrilaterals
The importance of Important Formulas: Quadrilaterals cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulas: Quadrilaterals Notes
Important Formulas: Quadrilaterals Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulas: Quadrilaterals.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulas: Quadrilaterals Notes on EduRev are your ultimate resource for success.
Important Formulas: Quadrilaterals Class 8 Questions
The "Important Formulas: Quadrilaterals Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulas: Quadrilaterals on the App
Students of Class 8 can study Important Formulas: Quadrilaterals alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulas: Quadrilaterals,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulas: Quadrilaterals is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup