Worksheet: Quadrilaterals | Worksheets with Solutions for Class 8 PDF Download
| Table of contents |

|
| 1. Multiple Choice Questions (MCQs) |

|
| 2. True/False |

|
| 3. Fill in the Blanks |

|
| 4. Very Short Answer Questions |

|
| 5. Answer the following questions: |

|
1. Multiple Choice Questions (MCQs)
Q1: Which of the following is not a property of a square?
(a) All angles are 90°
(b) Opposite sides are parallel
(c) Only one pair of sides is equal
Q2: What will be the sum of interior angles of a polygon having 8 sides?
(a) 720°
(b) 1080°
(c) 1260°
(d) 1440°
Q3: Which quadrilateral has exactly two distinct consecutive pairs of equal sides?
(a) Kite
(b) Rhombus
(c) Trapezium
(d) Square
Q4: The sides of a quadrilateral are in the ratio of 2:5:4:1. Find out the sum of the smallest and largest angles.
(a) 120°
(b) 180°
(c) 240°
(d) 360°
Q5: If the area of a square field is 144 sq m, then find the perimeter.
(a) 24 m
(b) 36 m
(c) 48 m
(d) 60 m
Q6: If the base of a triangle is 3 cm and the height is 6 cm, then find the area.
(a) 6 sq cm
(b) 9 sq cm
(c) 12 sq cm
(d) 18 sq cm
Q7: An isosceles trapezium has:
(a) Both pairs of opposite sides parallel
(b) Non-parallel sides equal in length
(c) Diagonals equal and perpendicular
(d) All sides equal in length
Q8: In a parallelogram:
(a) Only one pair of sides is parallel
(b) Opposite sides are equal
(c) Diagonals are always equal in length
(d) All angles are 90°
Q9: If the three angles of a quadrilateral are 70°, 90° and 120°, then find the measure of the fourth angle.
(a) 100°
(b) 75°
(c) 80°
(d) 60°
Q10: The measure of two adjacent angles of a parallelogram are in the ratio 2:3. Find the measure of each of the angles of a parallelogram.
(a) 72°, 108°
(b) 54°, 112°
(c) 68°, 99°
(d) 86°, 114°
2. True/False
Q1: A kite has all four sides equal.Q2: A square is a special type of rectangle and parallelogram.
Q3: The sum of the smallest and largest angles of a quadrilateral, with sides in the ratio 2:5:4:1, is 240°.
Q4: The perimeter of a square field, with an area of 144 sq m, is 48 m.
Q5: The area of a triangle with a base of 3 cm and height of 6 cm is 9 sq cm.
3. Fill in the Blanks
Q1: A polygon in which all sides and all angles are equal is called a __________ polygon.
Q2: The diagonals of a rectangle are equal in length and __________ each other.
Q3: In a parallelogram, adjacent angles are __________.
Q4: The diagonals of a rhombus bisect each other at __________ degrees.
Q5: A trapezium has at least __________ pair of opposite sides parallel.
4. Very Short Answer Questions
Q1: Can all the angles of a quadrilateral be right angles?Q2: The sum of all angles in a quadrilateral is equal to_____ right angles.
Q3: Name the quadrilateral whose diagonals are equal.
Q4: Each angle of a square measures ___°.
Q5: How many parallel lines are in a trapezium?
Q6: Which figure is equiangular and equilateral polygons?
Q7: It rhombus also satisfied the properties of a_______.
Q8: If the diagonals of a quadrilateral are perpendicular bisectors of each other then it is always a______.
5. Answer the following questions:
Q1: A room has a length of 10 m, breadth of 5m and height of 8 m. Find out the area of the room.
Q2: The length of one side of a rhombus is 6.5 centimeters and its altitude is 10 centimeter. if the length of one side of its diagonals is 26 centimeter find the length of the other diagonal.
Q3: If three angles of a trapezium is 50°, 130° and 120°. Then find the other angle.
Q4: If two adjacent angles of a parallelogram are in the ratio 2:3 Find all the angles of the parallelogram.
Q5: if the angles of a quadrilateral are in the ratio 3:6:8:13. The largest angle is?
Q6: diagonals of a quadrilateral ABCD bisect each other. If A=45°. Then B=?
Q7: The angles of a quadrilateral are x°, x+5°, x+10°, x+25°. Then find the value of x.
Q8: ABCD is a trapezium such that AB || CD, ∠A : ∠D = 2 : 1, ∠B : ∠C = 7 : 5, find the angles of the trapezium.

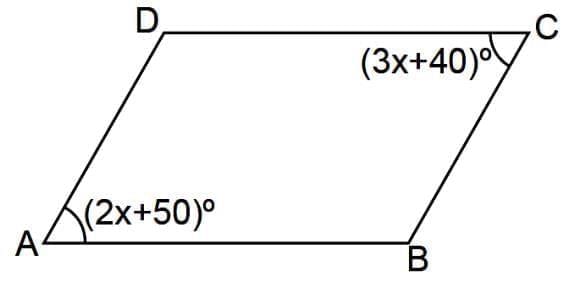
Q9: ABCD is a parallelogram where m∠A = (2x + 50°) and m∠C = (3x + 40°).
(i) Find the value of x.
(ii) Find the measure of each angle.
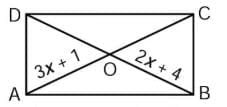
Q10: In the below figure, ABCD is a rectangle. Its diagonals meet at O. Find x, if OA = 3x + 1 and OB = 2x + 4.
You can access the solutions to this unit test here.
FAQs on Worksheet: Quadrilaterals - Worksheets with Solutions for Class 8
| 1. What are the properties of quadrilaterals? |  |
| 2. How do you classify quadrilaterals? |  |
| 3. What is the formula for calculating the area of different types of quadrilaterals? |  |
| 4. Can all quadrilaterals be cyclic? |  |
| 5. How can you find the missing angles in a quadrilateral? |  |




















