Short Question Answer: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1: In the given parallelogram ABCD, find the value of x and y.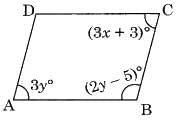 Ans:
Ans:
∠A + ∠B = 180°
3y + 2y – 5 = 180°
⇒ 5y – 5 = 180°
⇒ 5y = 180 + 5°
⇒ 5y = 185°
⇒ y = 37°
Now ∠A = ∠C [Opposite angles of a parallelogram] 3y = 3x + 3
⇒ 3 × 37 = 3x + 3
⇒ 111 = 3x + 3
⇒ 111 – 3 = 3x
⇒ 108 = 3x
⇒ x = 36°
Hence, x = 36° and y – 37°.
Q2: If one angle of a quadrilateral is 90° and the other three are equal, then each of the equal angles is:
a) 60°
b) 70°
c) 80°
d) 90°
Answer: c) 90°
Explanation: Let the equal angles be x. Then, 90° + 3x = 360°. So, 3x = 270° → x = 90°.
Q3: Find the values of x and y in the following parallelogram.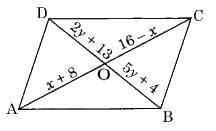 Ans:
Ans:
Since, the diagonals of a parallelogram bisect each other.
OA = OC
x + 8 = 16 – x
⇒ x + x = 16 – 8
⇒ 2x = 8
x = 4
Similarly, OB = OD
5y + 4 = 2y + 13
⇒ 3y = 9
⇒ y = 3
Hence, x = 4 and y = 3
Q4. Which of the following quadrilaterals always has its diagonals equal in length?
a) Parallelogram
b) Rhombus
c) Rectangle
d) Trapezium
Answer: c) Rectangle
Explanation: In a rectangle, diagonals are equal and bisect each other.
Q4: The sides AB and CD of a quadrilateral ABCD are extended to points P and Q respectively. Is ∠ADQ + ∠CBP = ∠A + ∠C? Give reason.
Ans: Join AC, then
∠CBP = ∠BCA + ∠BAC and ∠ADQ = ∠ACD + ∠DAC (Exterior angles of triangles)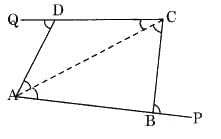 Therefore,∠CBP + ∠ADQ = ∠BCA + ∠BAC + ∠ACD + ∠DAC
Therefore,∠CBP + ∠ADQ = ∠BCA + ∠BAC + ∠ACD + ∠DAC
= (∠BCA + ∠ACD) + (∠BAC + ∠DAC)
= ∠C + ∠A
Q7. In a kite, which pair of angles are equal?
a) All four angles
b) Angles between unequal sides
c) Angles between equal sides
d) Opposite angles at the ends of diagonals
Answer: b) Angles between unequal sides
Explanation: In a kite, the pair of opposite angles between unequal sides are equal.
Q5: ABCD is a rhombus with ∠ABC = 126°, find the measure of ∠ACD.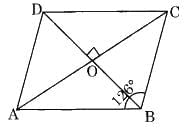 Ans: ∠ABC = ∠ADC (Opposite angles of a rhombus)
Ans: ∠ABC = ∠ADC (Opposite angles of a rhombus)
∠ADC = 126°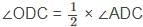
(Diagonal of rhombus bisects the respective angles)

⇒ ∠DOC = 90° (Diagonals of a rhombus bisect each other at 90°)
In ΔOCD,
∠OCD + ∠ODC + ∠DOC = 180° (Angle sum property)
⇒ ∠OCD + 63° + 90° = 180°
⇒ ∠OCD + 153° = 180°
⇒ ∠OCD = 180° – 153° = 27°
Hence ∠OCD or ∠ACD = 27°
Q6: The sum of the interior angles of a quadrilateral is always:
a) 180°
b) 270°
c) 360°
d) 540°
Answer: c) 360°
Explanation: For an n-sided polygon, sum of interior angles = (n – 2) × 180°. For a quadrilateral (n = 4): (4 – 2) × 180° = 360°.
Q7: Write true and false against each of the given statements.
(a) Diagonals of a rhombus are equal.
(b) Diagonals of rectangles are equal.
(c) Kite is a parallelogram.
(d) Sum of the interior angles of a triangle is 180°.
(e) A trapezium is a parallelogram.
(f) Sum of all the exterior angles of a polygon is 360°.
(g) Diagonals of a rectangle are perpendicular to each other.
(h) Triangle is possible with angles 60°, 80° and 100°.
(i) In a parallelogram, the opposite sides are equal.
Ans:
(a) False
(b) True
(c) False
(d) True
(e) False
(f) True
(g) False
(h) False
(i) True
Q8. Which quadrilateral has one pair of parallel sides?
a) Parallelogram
b) Rhombus
c) Trapezium
d) Square
Answer: c) Trapezium
Explanation: A trapezium has only one pair of parallel sides.
|
26 videos|177 docs|11 tests
|
FAQs on Short Question Answer: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the different types of quadrilaterals? |  |
| 2. What are the properties of a parallelogram? |  |
| 3. How do you calculate the area of different quadrilaterals? |  |
| 4. What is the sum of the interior angles of a quadrilateral? |  |
| 5. How can you distinguish between a kite and a rhombus? |  |
















