Unit Test (Solutions): Circles | Mathematics (Maths) Class 9 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question numbers 12 & 13 carry 5 marks each.
Q1. How many circles pass through three non-collinear points? (1 Mark)
(a) one
(b) two
(c) three
(d) four
Ans: (a)
Sol: Through any three non-collinear points, only one unique circle can pass.
Q2. What is the region enclosed between a chord and its corresponding arc called? (1 Mark)
(a) Radius
(b) Diameter
(c) Sector
(d) Segment
Ans: (d)
Sol: The area between a chord and its arc is called a segment.
Q3. What is the sum of opposite angles in a cyclic quadrilateral? (1 Mark)
(a) 90°
(b) 180°
(c) 360°
(d) 120°
Ans: (b)
Sol: In a cyclic quadrilateral, the sum of each pair of opposite angles is always 180°.
Q4. If a line segment subtends equal angles at two points on the same side of the line, what can be concluded? (1 Mark)
(a) The points are collinear
(b) The points lie on a circle
(c) The points form a square
(d) The points are equidistant
Ans: (b)
Sol: If a line segment subtends equal angles at two points on the same side, those four points are concyclic (i.e., they lie on the same circle).
Q5. What is the angle in a semicircle? (1 Mark)
(a) 45°
(b) 90°
(c) 180°
(d) 360°
Ans: (b)
Sol: The angle in a semicircle is always a right angle, i.e., 90°.
Q6. If a chord is perpendicular to the radius at its midpoint, what is the angle between the radius and the chord? (2 Marks)
Ans: If the radius of a circle is drawn to the midpoint of a chord, then it is perpendicular to the chord.
Hence, the angle between the radius and the chord is 90°.
Q7. State the converse of the theorem: “Angles in the same segment of a circle are equal.” (2 Marks)
Ans: Converse Theorem (Theorem 9.9):
If a line segment joining two points subtends equal angles at two other points on the same side of the line, then all four points lie on a circle.
⇒ The four points are concyclic.
Q8. In a cyclic quadrilateral ABCD, if ∠A = 95°, find ∠C and justify your answer. (2 Marks)
Ans: In a cyclic quadrilateral, opposite angles are supplementary.
⇒ ∠A + ∠C = 180°
⇒ ∠C = 180° – 95° = 85°
Q9. On a common hypotenuse AB, two right triangles, ACB and ADB, are situated on opposite sides. Prove that ∠BAC = ∠BDC. (3 Marks)
Ans: According to the question,
We have,
ACB and ADB are two right triangles.To Prove: ∠BAC = ∠BDC
We know that,ADBC forms a cyclic quadrilateral as ∠ACB and ∠ADB are 90° (angles in semicircles), and hence their sum = 180°.
In a circle, angles subtended by the same chord (AB) on the same side are equal.
⇒ ∠BAC = ∠BDCHence Proved.
Q10. ABCD is a parallelogram. The circle through A, B and C intersects (produce if necessary) at E. Prove that AE = AD. (3 Marks)
Ans:
Given: ABCD is a parallelogram. Circle through A, B and C intersects CD produced in E.
To Prove: AE = AD
Proof: ABCE is a cyclic quadrilateral.
∴ ∠B + ∠E = 180° …(i)
ABCD is a parallelogram.
∴ ∠B = ∠1 … (ii)
Also, ∠1 + ∠2 = 180° [linear pair]
∠B + ∠2 = 180° …(iii) [using (ii)]
Now, from (i) and (iii), we have
∠B + ∠E = ∠B + ∠2
∠E = ∠2
In ∆ADE,
∠E = ∠D (say ∠2), so sides opposite to equal angles are equal
⇒ AE = AD.
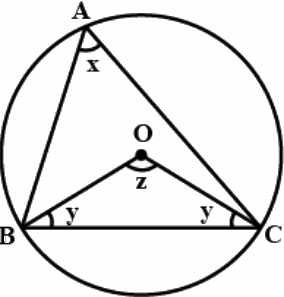
Q11. The circumcenter of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º. (3 Marks)
Ans: Let ∠BAC = x, ∠OBC = y
Then, ∠BOC = 2x (angle at centre is double)
In ∆OBC:
∠BOC + 2y = 180°
⇒ 2x + 2y = 180°
⇒ x + y = 90°
So, ∠BAC + ∠OBC = 90°
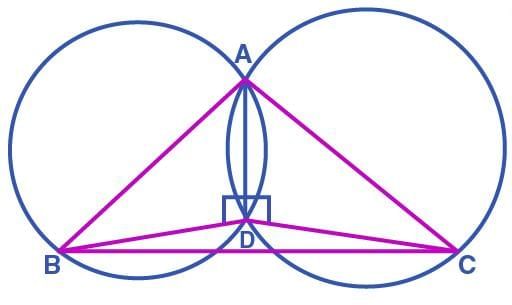
Q12. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lies on the third side. (5 Marks)
Ans: Given:
Two circles are drawn:
One with diameter ABAnother with diameter AC
These circles intersect at a point D (other than A)
To Prove: Point D lies on the line segment BC, i.e., D lies on the third side of triangle ABC.
Proof:
In the circle with diameter AB,
∠ADB = 90°
(Angle in a semicircle is a right angle)In the circle with diameter AC,
∠ADC = 90°
(Again, angle in a semicircle is 90°)So, in quadrilateral B–D–C,
∠ADB + ∠ADC = 90° + 90° = 180°Therefore, points B, D, and C lie on a straight line.
⇒ ∠BDC = 180° (Linear angle)Hence, point D lies on line BC, i.e., on the third side of triangle ABC.
Q13. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70° and ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD. (5 Marks)
Ans: Consider the following diagram -
Consider the chord CD,
As we know, angles in the same segment are equal.
So, ∠CBD = ∠CAD
∴ ∠CAD = 70°
Now, ∠BAD will be equal to the sum of angles BAC and CAD.
So, ∠BAD = ∠BAC + ∠CAD
= 30° + 70°
∴ ∠BAD = 100°
As we know, the opposite angles of a cyclic quadrilateral sum up to 180 degrees.
So,
∠BCD + ∠BAD = 180°
Since, ∠BAD = 100°
So, ∠BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠BCA = ∠CAB (Angles opposite to equal sides of a triangle)
∠BCA = 30°
also, ∠BCD = 80°
∠BCA + ∠ACD = 80°
So, ∠ACD = 50° and,
∠ECD = 50°
|
40 videos|470 docs|56 tests
|
FAQs on Unit Test (Solutions): Circles - Mathematics (Maths) Class 9
| 1. What are the properties of circles that are important for solving problems in Class 9 mathematics? |  |
| 2. How do you calculate the circumference and area of a circle? |  |
| 3. What is the significance of theorems related to circles in Class 9 geometry? |  |
| 4. How can one apply the properties of tangents to solve problems involving circles? |  |
| 5. What types of questions can be expected in exams regarding circles in Class 9? |  |