Metre (m) is used for larger measurements (e.g., height of India Gate, depth of a well).
Centimetre (cm) is used for smaller measurements (e.g., length of a handkerchief, distance between buttons).
The appropriate unit is chosen based on the size of the object or distance.
Class 5 Exam > Class 5 Notes > Mathematics (Maths Mela) Class 5 - New NCERT > Chapter Notes: Far and Near
Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
Have you ever wondered how we measure the height of a tree, the length of a ribbon, or the distance to another city? We cannot use the same unit for all these!
In this chapter Far and Near, we will:
Discover which unit—mm, cm, m, or km—is best for different measurements.
Learn how to change one unit into another.
Try fun activities like measuring saris, sprout lengths, and even the tallest statues in the world.
Explore how distances are measured in real life—on playgrounds, train journeys, and even in races.
Let’s start with a quick identification
Identify the appropriate units for measuring each of the following.
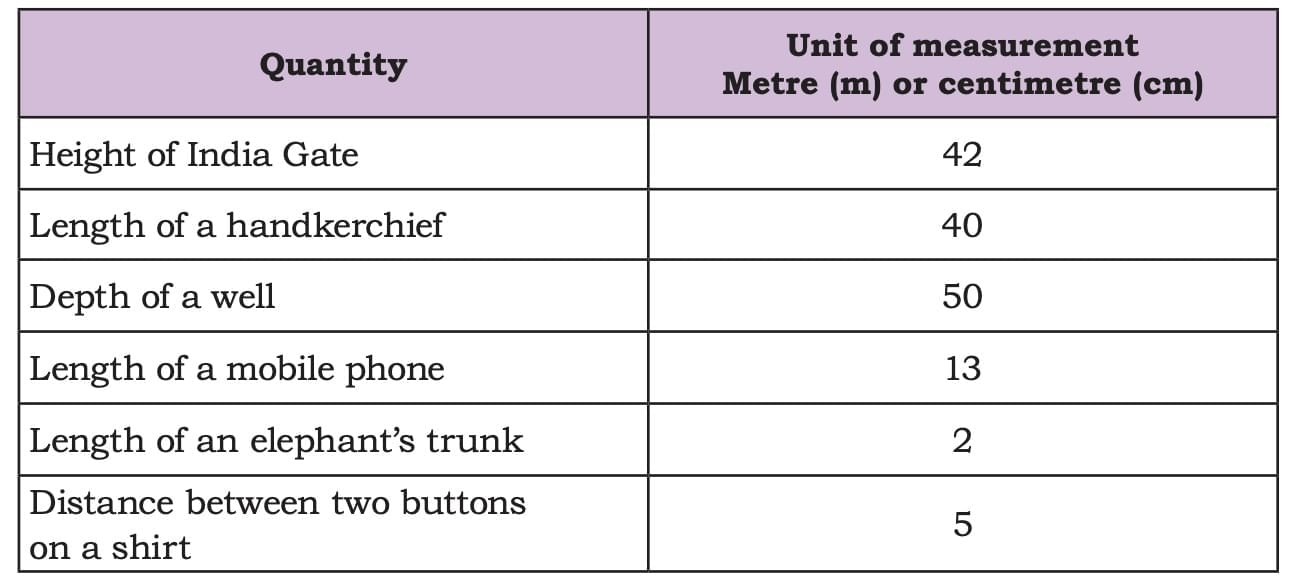
In conclusion, we can say that:
Different Units but Same Measure
We often use different units (like centimetres and metres) to measure the same length.
1 metre (m) = 100 centimetres (cm).
Let’s Understand with a Story
Riya and Aman were playing in their garden. Riya had a rope that was 200 cm long. 
Aman said, “200 cm sounds too big! Can we say it in metres instead?”
Riya thought for a while. She remembered what her teacher had said:
So she quickly divided 200 by 100.
“Look, Aman! 200 cm is the same as 2 metres.”
Just then, Aman brought another rope of 500 cm.
He asked, “How long is this in metres?”
Riya smiled, “That’s easy! 500 ÷ 100 = 5 metres.”
Both ropes together measured 7 metres in total!
Now, let’s connect centimetres and metres on a number line to clearly see how the conversion works.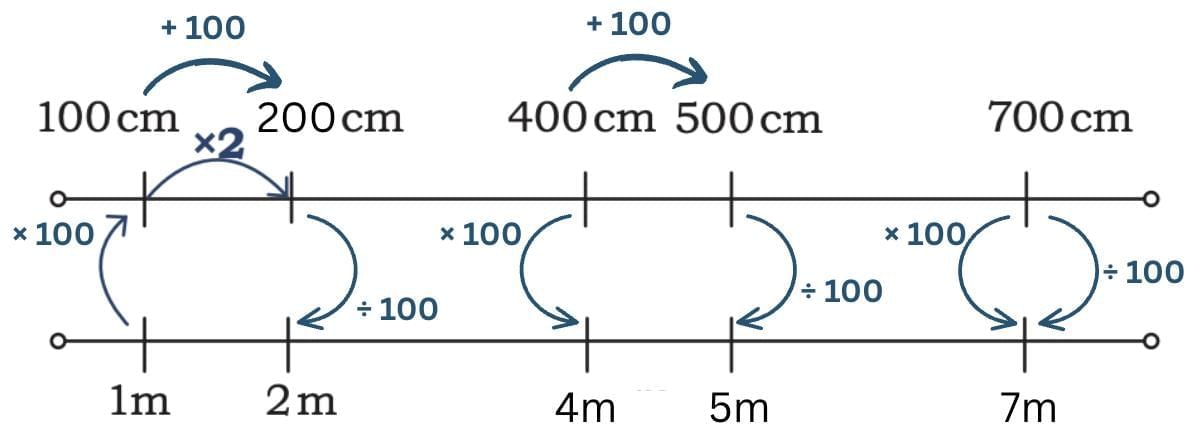
Let Us Compare
We can compare two or more lengths using the symbols < (less than), > (greater than), or = (equal to).
General Rules:
Convert units to the same form before comparing.: (Either convert everything to cm or everything to m).
Use 1 m = 100 cm to change units.
Simplify the numbers by adding or converting if required.
Compare the values directly using <, >, or =.
Remember:
1 m = 100 cm
If numbers are equal → use =
If one is bigger → use > or < accordingly.
Examples:
(a) 456 cm ____ 5 m
Convert 5 m = 500 cm.
Compare: 456 cm < 500 cm.
(b) 55 cm + 200 cm ____ 200 cm + 54 cm
Left side = 255 cm, Right side = 254 cm.
Compare: 255 cm > 254 cm.
Measuring Long Distances
For very long distances, we use special tools and units. We often use kilometre (km) for long distances.
Here are some ways to measure long distances:
• Long Tape: A very long measuring tape.
• Rangefinder: A device that measures distance to a target.
• Laser Distance Meter: Uses a laser to measure distance.
• Rodometer (measuring wheel): A wheel that measures distance as it rolls.
Question for Chapter Notes: Far and NearTry yourself: What unit do we often use for long distances?View Solution
Let Us Explore
When we walk 1,000 metres, we say we have walked 1 kilometre (1 km).
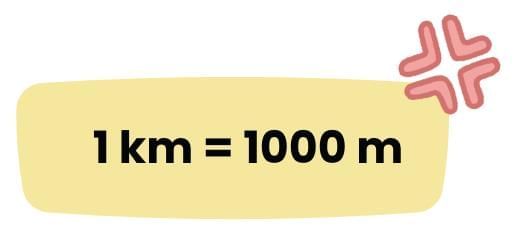
The prefix ‘kilo’ means thousand.
Kilometres are used to measure long distances like:
Distance between two cities
Length of a road
Distance travelled in a vehicle
Let’s practice some examples
1. Convert kilometres to metres
3 km = 3 × 1000 m = 3000 m
7 km = 7 × 1000 m = 7000 m
2. Convert metres to kilometres
5000 m = 5000 ÷ 1000 = 5 km
2300 m = 2300 ÷ 1000 = 2 km 300 m
The World of Small Things
Some objects, like sprouts, small screws, and nails, are very small in size.
To measure such small things, we use the smaller marks on a scale (ruler).
- We use a smaller unit called millimetre (mm).
Between 1 cm and 2 cm on a scale, there are 10 equal small divisions.
Each small division is called 1 millimetre (mm).
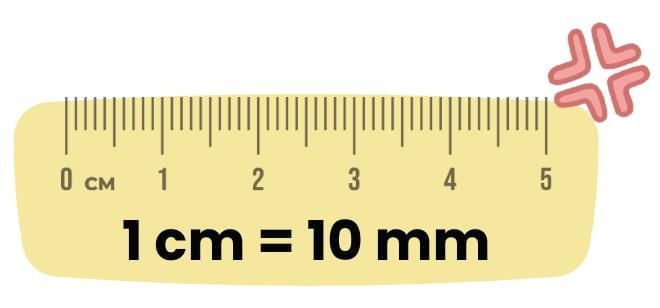
These smaller marks allow us to measure lengths more precisely.
Relationships between Different Units
Let's summarise the relationships between different units of length:
• 10 mm = 1 cm (Millimetre to Centimetre)
• 100 cm = 1 m (Centimetre to Metre)
• 1,000 m = 1 km (Metre to Kilometre)
Question for Chapter Notes: Far and NearTry yourself: How many millimeters are in one centimeter?View Solution
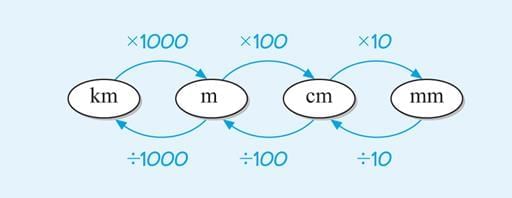
Adding and Subtracting Lengths
We can add and subtract lengths just like we add and subtract numbers. We need to be careful with units.
1. Adding Lengths
Example 1: Saji walked 3 km 450 m in the morning and 4 km 650 m in the evening. How much did he walk in total?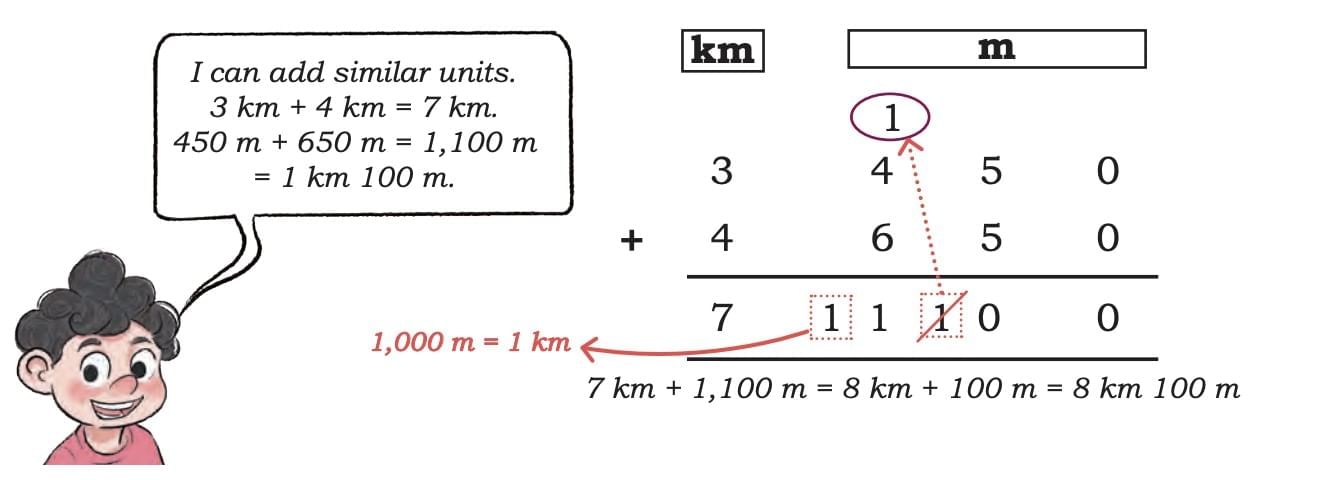
Let's take a look at both the methods
Method 1: Adding km and m separately
- Add kilometres: 3 km + 4 km
= 7 km. - Add metres: 450 m + 650 m
= 1100 m. - Convert 1100 m to km and m
= 1000 m + 100 m
= 1 km 100 m. - Add the converted metres to kilometres
7 km + 1 km 100 m
= 8 km 100 m.
Method 2: Convert everything to metres and then add
- Convert 3 km 450 m
= 3 x 1000 m + 450 m
= 3000 m + 450 m
= 3450 m. - Convert 4 km 650 m
= 4 x 1000 m + 650 m
= 4000 m + 650 m
= 4650 m. - Total distance = 3450 m + 4650 m = 8100 m.
- Convert 8100 m to km and m
= 8000 m + 100 m
= 8 km 100 m.
2. Subtracting Lengths
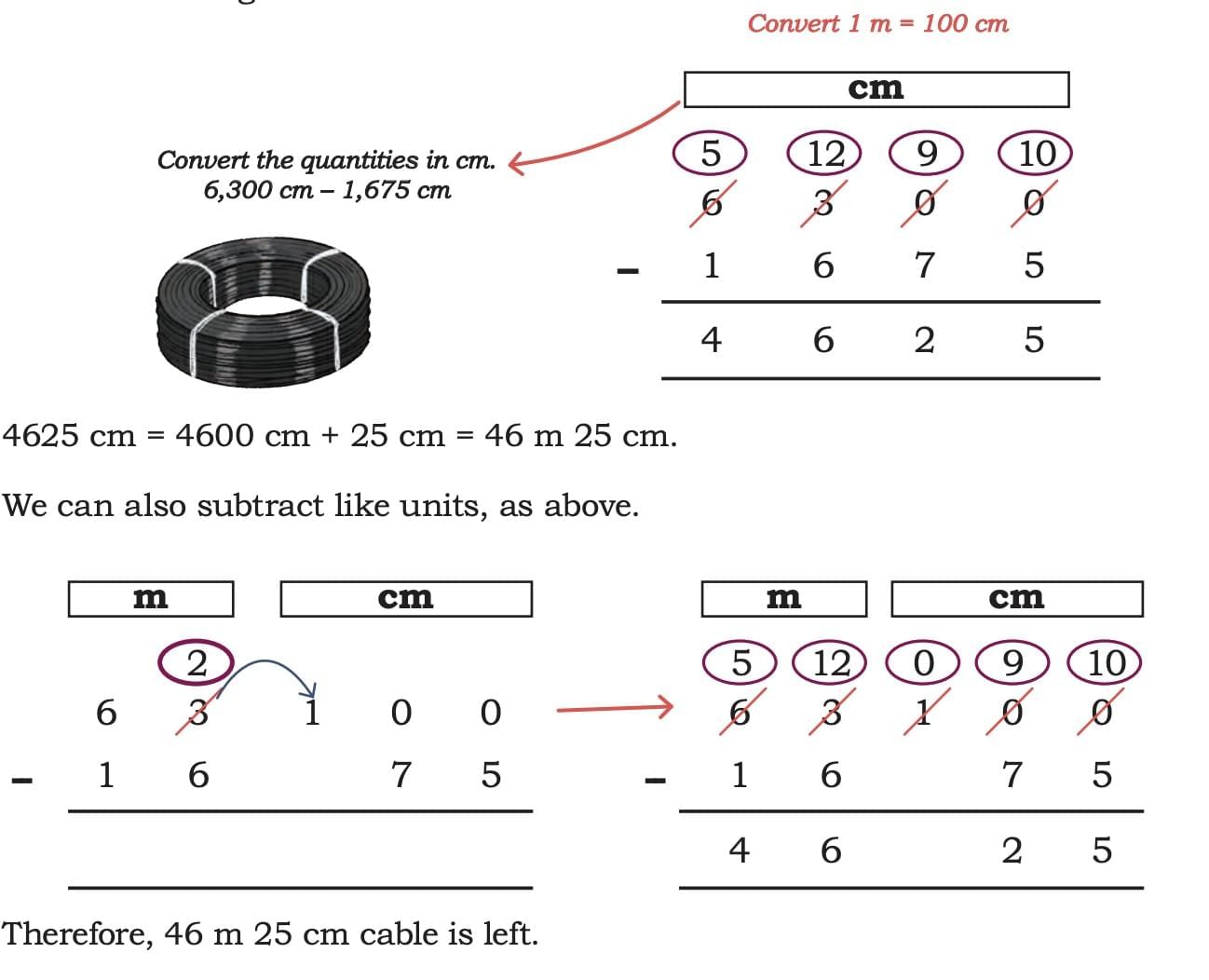
Example 2: Electricians are changing the cables in a house. They need 63m of cable for this purpose. They used 16m 75cm cable in the first room. What is the length of the cable left?
Let's take a look at both the methods
Electricians need 63 m of cable. They used 16 m 75 cm in the first room.Method 1: Convert everything to cm and then subtract
- Total cable needed: 63 m
= 63 x 100 cm
= 6300 cm. - Cable used: 16 m 75 cm
= 16 x 100 cm + 75 cm
= 1600 cm + 75 cm
= 1675 cm. - Cable left
= 6300 cm - 1675 cm
= 4625 cm. - Convert 4625 cm to m and cm
= 4600 cm + 25 cm
= 46 m 25 cm.
Method 2: Subtracting m and cm separately (with borrowing)
Step 1: Arrange in Columns
Step 2: Notice the Borrowing
We cannot directly subtract 75 from 00 cm.
So, we borrow 1 metre (m) = 100 cm.
Now, 63 m becomes 62 m, and centimetres become 200 cm (100 already + borrowed 100).
Step 3: Subtract Normally
Centimetres: 200 - 75 = 125 cm
Metres: 62 - 16 = 46 m
Step 4: Convert if Needed
Since 100 cm = 1 m,
125 cm = 1 m 25 cm
So,
46 m 125 cm = 46 m 25 cm
Multiplying and Dividing Lengths
We can also multiply and divide lengths to find total or equal parts.
Multiplying lengths helps when the same length is used many times, like cloth for several shirts or ribbon pieces.
Dividing lengths helps when we need to share a length into equal parts, like cutting a rope into equal pieces.
1. Multiplying Lengths
Example 1: We need a 1 m 80 cm cloth to make a shirt for a 10-year-old child. How much cloth will be needed to make shirts for 20 such children?
Given:
Cloth for 1 child’s shirt = 1 m 80 cm
For 20 children, we multiply.
Let's take a look at the methods to solve
Method 1: Break and Multiply
Step 1: Break into metres and centimetres.
1 m 80 cm = 1 m + 80 cm
Step 2: Multiply separately.
20 × 1 m = 20 m
20 × 80 cm = 1600 cm
Step 3: Convert cm into metres.
1600 cm = 16 m
Step 4: Add together.
20 m + 16 m = 36 m
Method 2: Convert everything to cm and then multiply
Step 1: Convert to cm:
- 1 m 80 cm = 100 cm + 80 cm
= 180 cm
Step 2: Multiply by 20 shirts:
- Total cloth = 20 × 180 cm = 3600 cm
Step 3: Convert cm to metres:
- 3600 cm = 36 × 100 cm = 36 m
2. Dividing Lengths
Example 2: A shop sells cloth for making bags at ₹100 for 5 m. How much money is needed to buy a 1 m cloth?
If 5 m cloth costs ₹100, then a 1 m cloth costs 100 ÷ 5 = ₹20.
- A shop sells cloth for ₹100 for 5 m. How much money is needed to buy 1 m cloth?
- Cost of 5 m cloth = ₹100.
- Cost of 1 m cloth = ₹100 ÷ 5
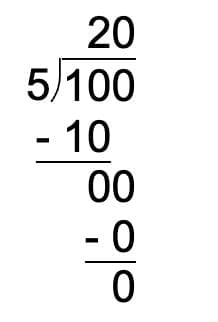
- Therefore, the cost of 1m of cloth is 20m
Question for Chapter Notes: Far and NearTry yourself: How much cloth is needed for 20 children if one shirt requires 1 m 80 cm?View Solution
Let Us Estimate
- Estimating means making a good guess about a measurement without actually measuring it.
- We use things we already know as a reference.
Let's understand this with the help of an example:
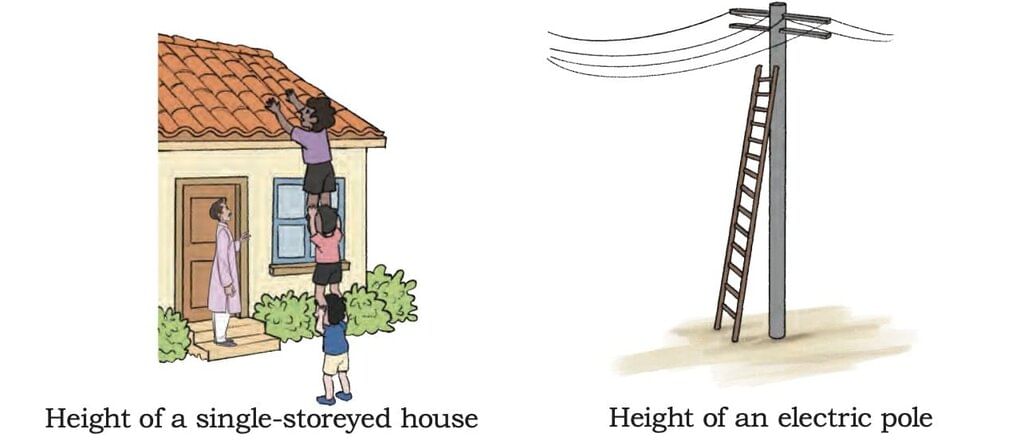
Height of a single-storeyed house: You can estimate it to be around 3-4 metres.
Height of an electric pole: You can estimate it to be around 8-10 metres.
Practice Questions
Tallest building in your neighbourhood
If one floor ≈ 3 metres, then a 5-storey building ≈ 15 metres.
Reference: single-storeyed house.
Tallest tree in your neighbourhood
Compare with electric pole (about 8–10 m).
If tree is a little taller, estimate ≈ 12–15 metres.
Quick Tip: Always compare with something you already know (like your own height or a nearby house) to estimate correctly.
Let Us Explore (Feet and Inches)
In daily life, we also use other units for measuring length, especially for height. These are feet (ft) and inches (in).
Look at your ruler. Some rulers also have inches marked on them.
• 1 inch = approximately 2 cm 5 mm (or 2.5 cm)
• 1 foot = 12 inches
• 1 foot = approximately 30 cm
The document Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT is a part of the Class 5 Course Mathematics (Maths Mela) Class 5 - New NCERT.
All you need of Class 5 at this link: Class 5
|
35 videos|318 docs|7 tests
|
FAQs on Far and Near Chapter Notes - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are different units used to measure lengths and distances? |  |
Ans.Length and distance can be measured using various units such as millimeters (mm), centimeters (cm), meters (m), and kilometers (km). Each unit represents a different scale of measurement, with millimeters being the smallest common unit and kilometers being used for larger distances.
| 2. How do we convert between different units of length? | |
Ans.To convert between different units of length, you can use conversion factors. For example, 1 meter is equal to 100 centimeters and 1 kilometer is equal to 1,000 meters. By multiplying or dividing the length by these conversion factors, you can switch between units easily.
| 3. Why is it important to measure long distances accurately? | |
Ans.Accurate measurement of long distances is crucial for various reasons, including navigation, construction, and mapping. It helps in ensuring safety, efficiency, and precision in activities such as traveling, building infrastructure, and conducting scientific research.
| 4. How do we add and subtract lengths in different units? | |
Ans.When adding or subtracting lengths in different units, you first need to convert them to the same unit. For example, if you have 2 meters and 150 centimeters, convert 150 cm to meters (which is 1.5 m) and then add: 2 m + 1.5 m = 3.5 m.
| 5. What are some practical examples of measuring small things and their significance? | |
Ans.Measuring small things, such as in millimeters or centimeters, is important in fields like engineering, biology, and manufacturing. For instance, in engineering, precise measurements can impact the functionality of machinery, while in biology, measuring cells and microorganisms accurately is essential for research and experiments.
About this Document
4.69/5
Rating
Sep 19, 2025
Last updated
Related Exams
Document Description: Chapter Notes: Far and Near for Class 5 2025 is part of Mathematics (Maths Mela) Class 5 - New NCERT preparation.
The notes and questions for Chapter Notes: Far and Near have been prepared according to the Class 5 exam syllabus. Information about Chapter Notes: Far and Near covers topics
like Different Units but Same Measure, Let Us Compare, Measuring Long Distances, Let Us Explore, The World of Small Things, Relationships between Different Units, Adding and Subtracting Lengths, Multiplying and Dividing Lengths, Let Us Estimate, Let Us Explore (Feet and Inches) and Chapter Notes: Far and Near Example, for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Chapter Notes: Far and Near.
Introduction of Chapter Notes: Far and Near in English is available as part of our Mathematics (Maths Mela) Class 5 - New NCERT
for Class 5 & Chapter Notes: Far and Near in Hindi for Mathematics (Maths Mela) Class 5 - New NCERT course.
Download more important topics related with notes, lectures and mock test series for Class 5
Exam by signing up for free. Class 5: Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT
Description
Full syllabus notes, lecture & questions for Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT - Class 5 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths Mela) Class 5 - New NCERT | Best notes, free PDF download
Information about Chapter Notes: Far and Near
In this doc you can find the meaning of Chapter Notes: Far and Near defined & explained in the simplest way possible. Besides explaining types of
Chapter Notes: Far and Near theory, EduRev gives you an ample number of questions to practice Chapter Notes: Far and Near tests, examples and also practice Class 5
tests
Related Searches
video lectures
,Previous Year Questions with Solutions
,Semester Notes
,ppt
,MCQs
,practice quizzes
,Free
,mock tests for examination
,Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT
,Important questions
,past year papers
,Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT
,Sample Paper
,Extra Questions
,Objective type Questions
,Summary
,study material
,Exam
,shortcuts and tricks
,Viva Questions
,Far and Near Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT
;
Additional Information about Chapter Notes: Far and Near for Class 5 Preparation
Chapter Notes: Far and Near Free PDF Download
The Chapter Notes: Far and Near is an invaluable resource that delves deep into the core of the Class 5 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Chapter Notes: Far and Near now and kickstart your journey towards success in the Class 5 exam.
Importance of Chapter Notes: Far and Near
The importance of Chapter Notes: Far and Near cannot be overstated, especially for Class 5 aspirants.
This document holds the key to success in the Class 5 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Chapter Notes: Far and Near
Chapter Notes: Far and Near Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Chapter Notes: Far and Near.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Chapter Notes: Far and Near Notes on EduRev are your ultimate resource for success.
Chapter Notes: Far and Near Class 5 Questions
The "Chapter Notes: Far and Near Class 5 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 5 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Chapter Notes: Far and Near on the App
Students of Class 5 can study Chapter Notes: Far and Near alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Chapter Notes: Far and Near,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Chapter Notes: Far and Near is prepared as per the latest Class 5 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily