We are the Travellers NCERT Solutions | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
| Table of contents |

|
| Page 3 – 4 |

|
| Page 5 – 7 |

|
| Page 8 – 9 |

|
| Page 10 |

|
| Finding Large Numbers Around Us |

|
| Page 11 - 12 |

|
| Pastime Mathematics |

|
| Page 13 - 15 |

|
Page 3 – 4
Q. Let us see how we write numbers beyond 10,000 and how we name them. We write them in the same way as numbers below 9,999. You can use the tokens given in the end of the book.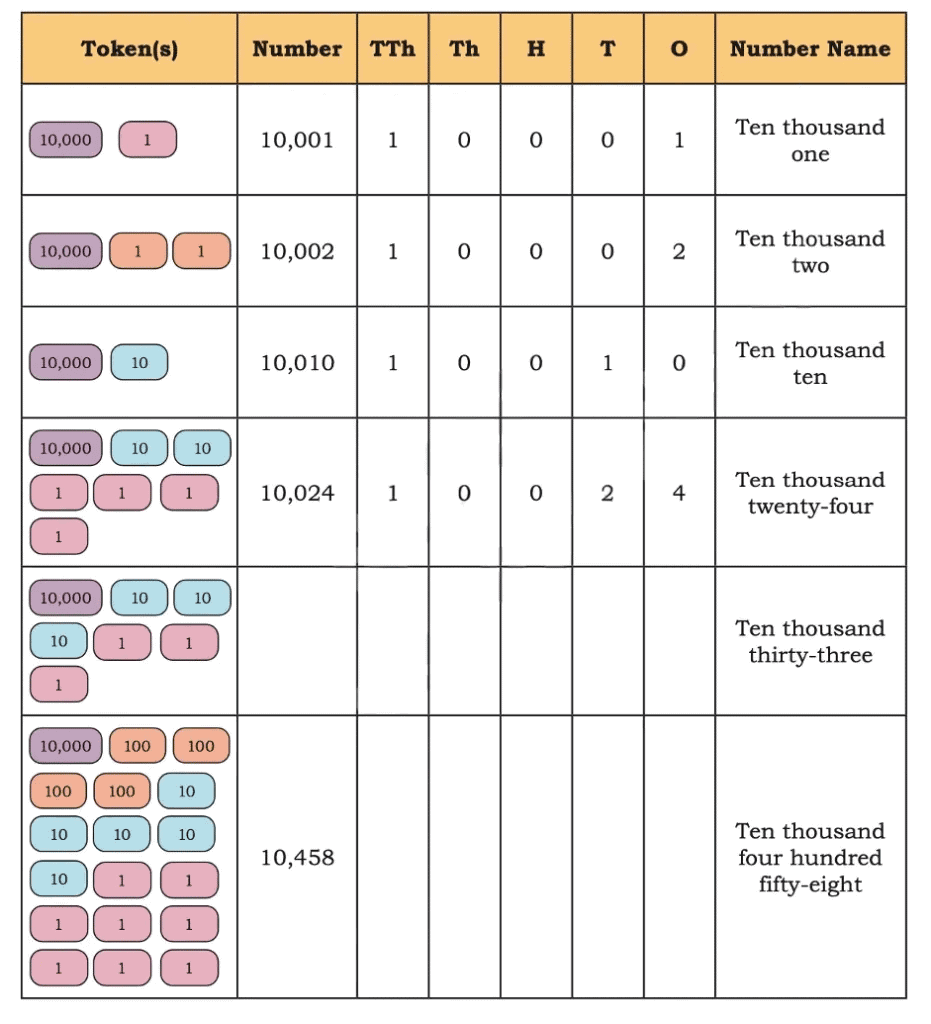
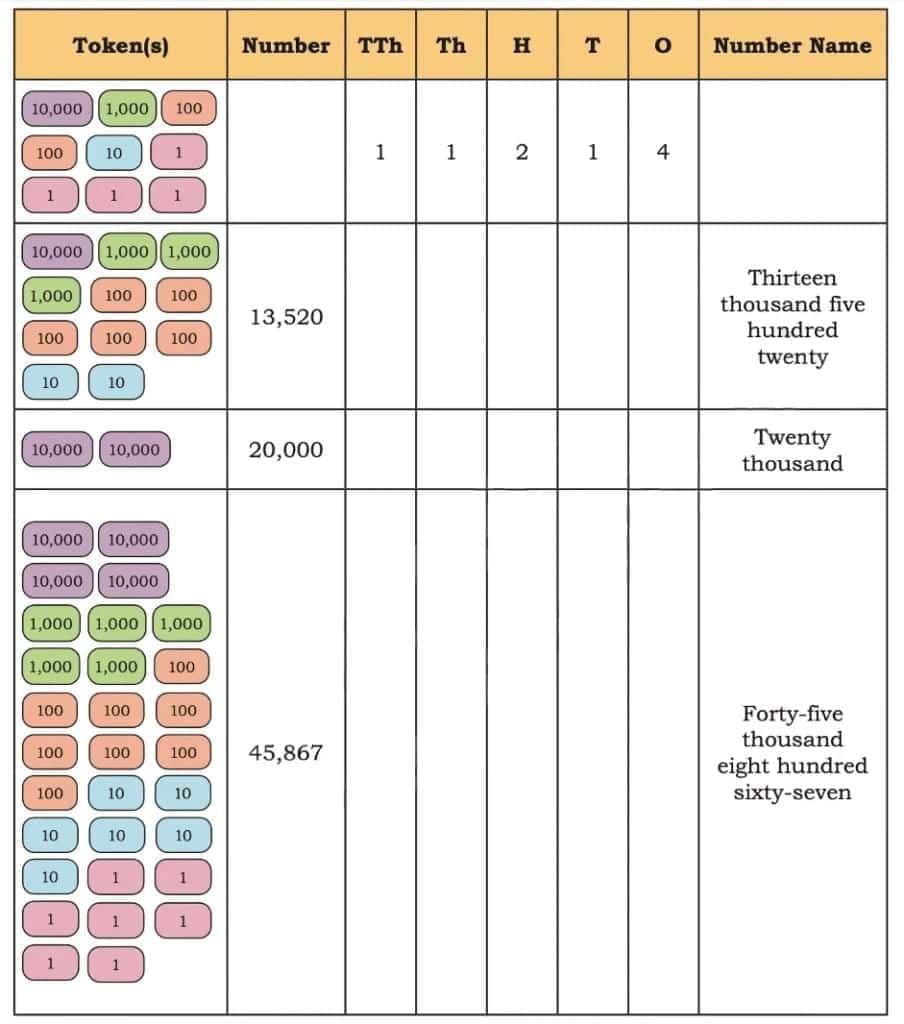 Ans:
Ans: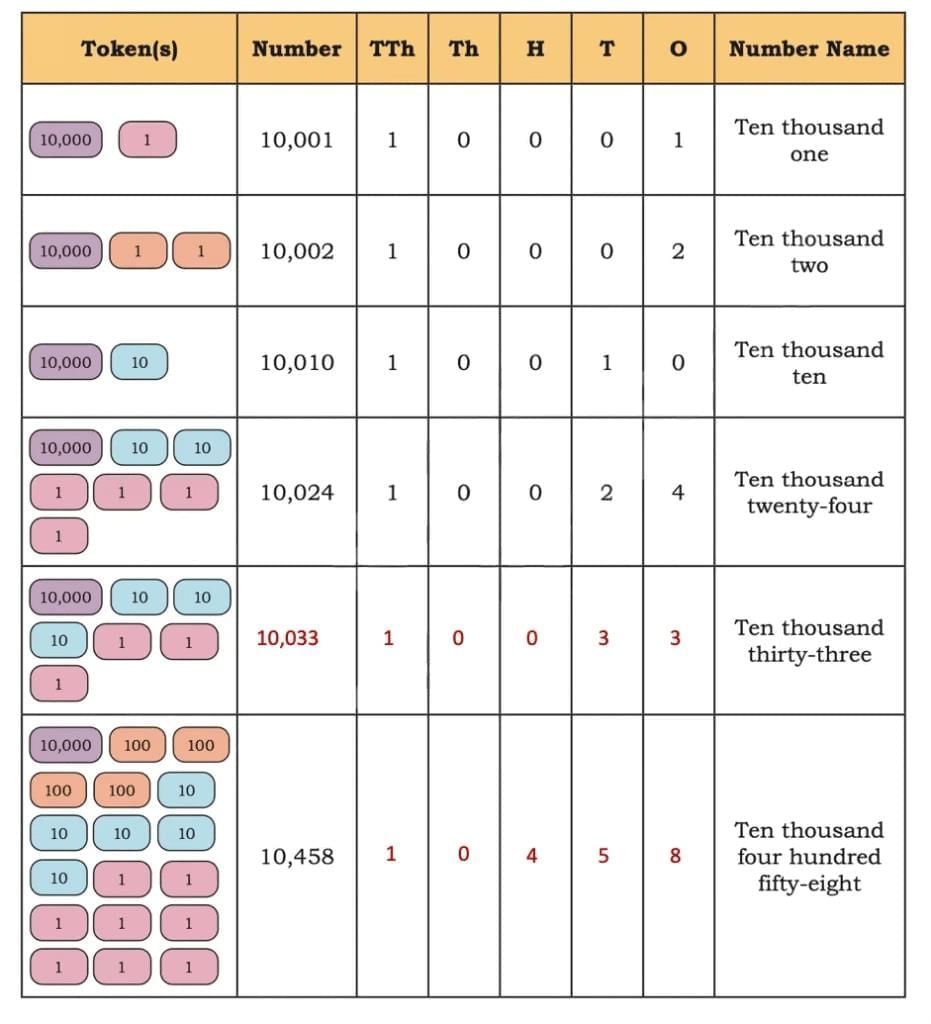

Page 5 – 7
Let Us Do
Q1. Fill in the blanks by continuing the pattern in each of the following sequences. Discuss the patterns in class.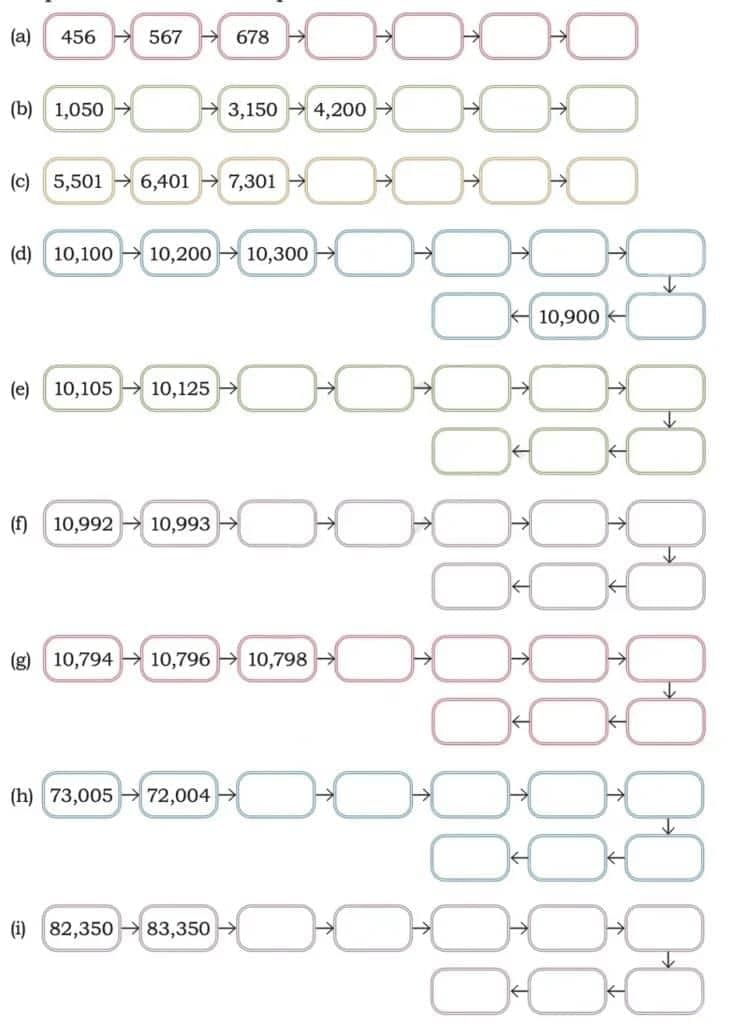 Ans:
Ans:
Q2. Fill in the blanks appropriately. Use commas as required.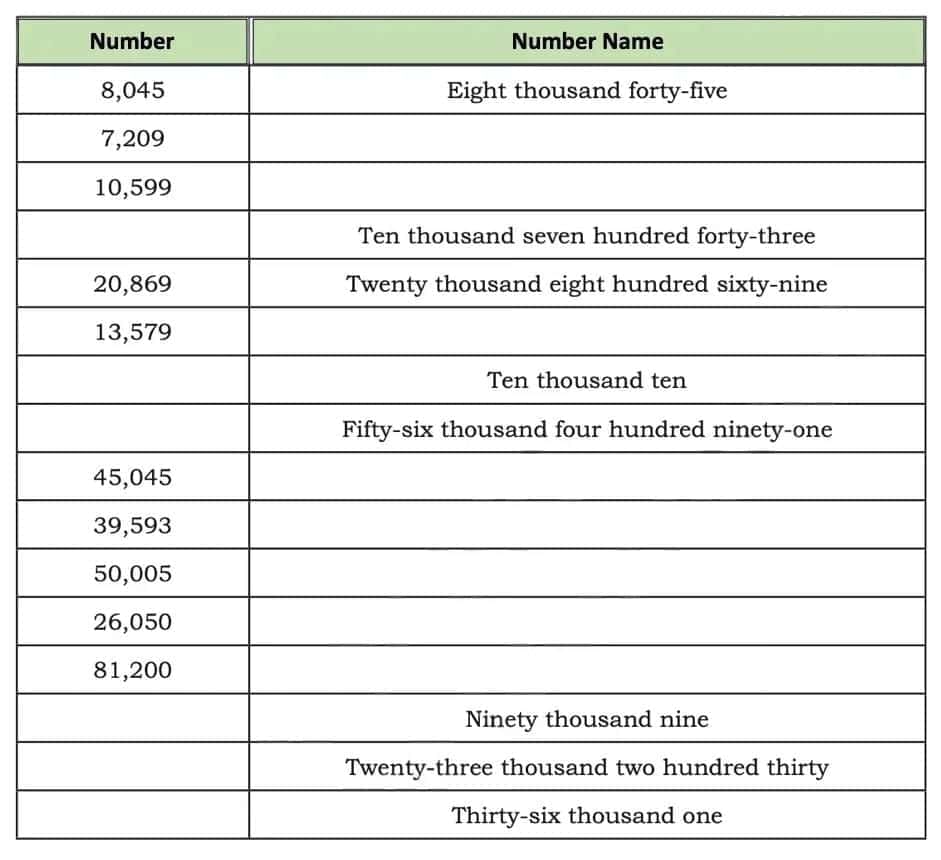 Ans:
Ans: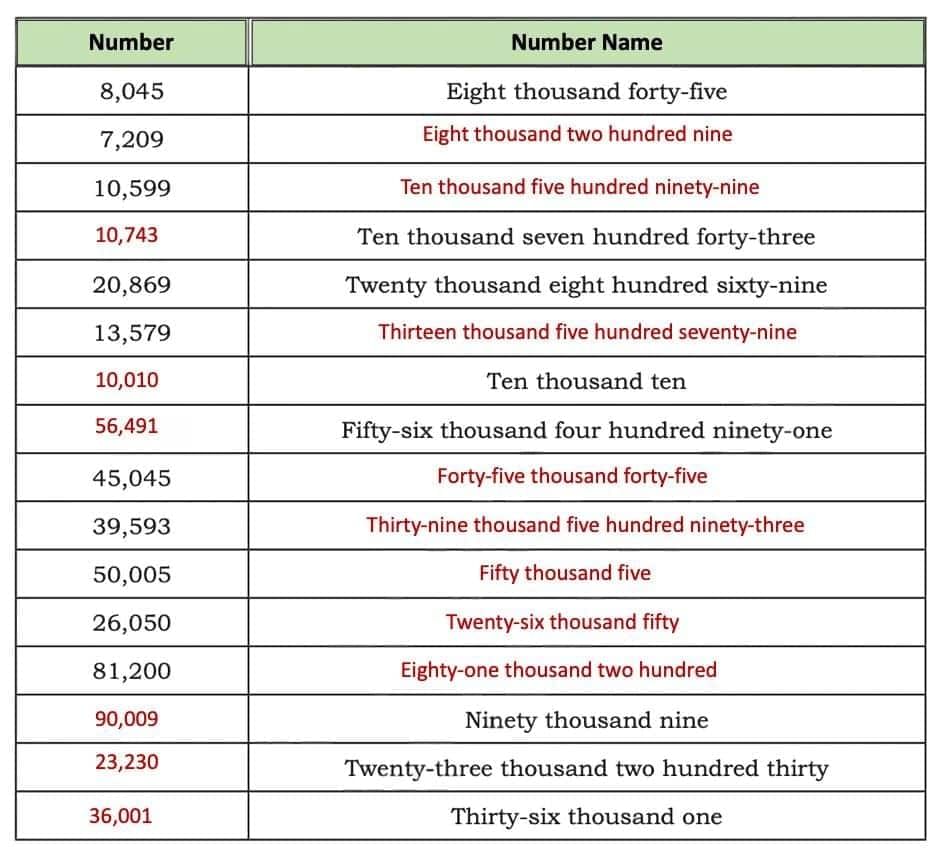
Q3. Arrange the numbers below in increasing order. You can use the number line below, if required. Ans:
Ans: 
Q4. A student said 9,990 is greater than 49,014 because 9 is greater than 4. Is the student correct? Why or why not? Use the number line below to find the position of the numbers. Fill in the blanks. Ans: No, the student is incorrect. It’s true that 9 is greater than 4 but comparing only the first digit of two numbers doesn’t always give the correct answer. You must compare the entire numbers starting from the leftmost digit and also consider how many digits the numbers have.
Ans: No, the student is incorrect. It’s true that 9 is greater than 4 but comparing only the first digit of two numbers doesn’t always give the correct answer. You must compare the entire numbers starting from the leftmost digit and also consider how many digits the numbers have.
Here,
9,990 is a four-digit number.
49,014 is a five-digit number.
So, 49,014 is greater than 9,990.
Q5. Digit swap
(a) In the number 1,478, interchanging the digits 7 and 4 gives 1,748. Now, interchange any two digits in the number 1,478 to make a number that is larger than 5,500
(b) Interchange two digits of 10,593 to make a number
(i) Between 11,000 and 15,000.
(ii) More than 35,000.
(c) Interchange two digits of 48,247 to make a number
(i) As small as possible.
(ii) As big as possible.
Ans: (a) Number – 1478
Interchanging the digits 1 and 7 gives 7418, which is greater than 5500.
(b) Number – 10,593
(i) Interchanging the digits 0 and 3 gives 13,590, which lies between 11,000 and 15,000.
(ii) Interchanging the digits 1 and 5 gives 50,193, which is more than 35,000.
(c) Number – 48,247
(i) Interchanging the digits 4 and 2 gives 28,447.
So, 28,447 is the smallest number.
(ii) Interchanging the digits 4 and 8 gives 84,247.
So, 84,247 is the largest number.
Page 8 – 9
Q. The rabbit is at 2,346. Its food has been kept at its neighbouring hundreds. Which of the two hundreds should the rabbit go to? _______ is the nearest hundred of 2,346. It will need ______ jumps to reach ______. Ans: 2,300 is the nearest hundred of the 2,346. It will need 46 jumps to reach 2,300.
Ans: 2,300 is the nearest hundred of the 2,346. It will need 46 jumps to reach 2,300.
Q. The rabbit is at 2,346. Its food has been kept at its neighbouring thousands. Which number should the rabbit go to? _________ is the nearest thousand of 2,346. It will need _______ jumps to reach ______. Ans: 2,000 is the nearest thousand of 2,346. It will need 346 jumps to reach 2000.
Ans: 2,000 is the nearest thousand of 2,346. It will need 346 jumps to reach 2000.
Q. Fill in the boxes appropriately

Ans: 
Let Us Think
Q1. Vijay rounded off a number to the nearest hundred. Suma rounded off the same number to the nearest thousand. Both got the same result. Circle the numbers they might have used. Ans: (i) 7,126
Ans: (i) 7,126
Nearest Hundred → 7,100
Nearest Thousand → 7,000
Results are different.
(ii) 7,835
Nearest Hundred → 7,800
Nearest Thousand → 8,000
Results are different.
(iii) 7,030
Nearest Hundred → 7,000
Nearest Thousand → 7,000
Results are same.
(iv) 6,999
Nearest Hundred → 7,000
Nearest Thousand → 7,000
Results are same.

Q2. Think and write two numbers that have the same—
(a) Nearest ten.
(b) Nearest hundred.
(c) Nearest thousand.
Ans: (a) Nearest ten: 42 and 45
Both round to the nearest ten = 40.
(b) Nearest hundred: 362 and 398
Both round to the nearest hundred = 400.
(c) Nearest thousand: 1,450 and 1,499
Both round to the nearest thousand = 1,000.
Q3. Think and write the numbers that have the same—
(a) Nearest ten and nearest hundred.
(b) Nearest hundred and nearest thousand.
(c) Nearest ten, hundred and thousand.
Ans: (a) 100
Nearest ten = 100
Nearest hundred = 100
(b) 950
Nearest hundred = 1000
Nearest thousand = 1000
(c) 1002
Nearest ten = 1000
Nearest hundred = 1000
Nearest thousand = 1000
Page 10
Q1. A cyclist can cover 15 km in one hour. How much distance will she cover in 4 hours, if she maintains the same speed?
Ans: Distance covered in one hour = 15 km.
Distance covered in five hours = 15 × 4 = 60 km.
Q2. A school has 461 girls and 439 boys. How many vehicles are needed for all of them to go on a trip using the following modes of travel? The numbers in the bracket indicates the number of people that can travel in one vehicle.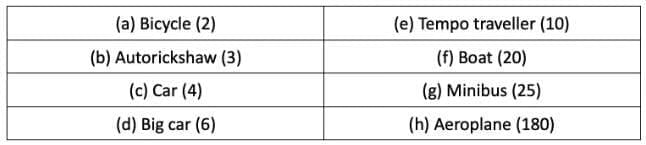 Ans: Girls = 461
Ans: Girls = 461
Boys = 439
Total = 461 + 439 = 900 students
(i) Number of people that can travel on a bicycle = 2
Total bicycles needed for all students = 900 ÷ 2 = 450 bicycles.
(ii) Number of people that can travel on an autorickshaw = 3
Total autorickshaws needed for all students = 900 ÷ 3 = 300.
(iii) Number of people that can travel in a car = 4
Total cars needed for all students = 900 ÷ 4 = 225.
(iv) Number of people that can travel in a big car = 6
Total big cars needed for all students = 900 ÷ 6 = 150.
(v) Number of people that can travel in a tempo traveller = 10
Total tempo traveller needed for all students = 900 ÷ 10 = 90.
(vi) Number of people that can travel in a boat = 20
Total boats needed for all students = 900 ÷ 20 = 45.
(vii) Number of people that can travel in a minibus = 25
Total minibuses needed for all students = 900 ÷ 25 = 36.
(viii) Number of people that can travel in an aeroplane = 180
Total aeroplanes needed for all students = 900 ÷ 180 = 5.
Finding Large Numbers Around Us
We saw that the distance (in kilometre) covered by different means of transport in an hour can range from a 1-digit number to a 5-digit number. Can we find other contexts around us that contain numbers in this range? Let us consider the situation below.
A book has around 200 pages, and each page has about 50 words. The book therefore has about 10,000 words in all.
Find something in the textbook whose count is a 4-digit number.
Now, let us try this with our school.
(a) Our school has ________ classrooms.
(b) There are ________ students in my class.
(c) Our classroom has ________ books in total.
Ans: Do it Yourself
Page 11 - 12
Q. Find something in the classroom whose count is a—
(i) 4-digit number.
(ii) 5-digit number.
Ans: (i) 4-digit number:
Example: Total number of pencils in the classroom
- If there are 1,000 pencils in a large classroom set or more classrooms combined, that would be a 4-digit number: 1,000 pencils.
(ii) 5-digit number:
Example: Total number of students in a school with multiple classrooms
A school with about 10 to 20 classrooms, each having an average of 30-50 students, might have a total student count that exceeds 10,000, for example: 15,000 students.
Q. List some quantities whose count is a 4-digit or a 5-digit number in the context of—
(i) A tree.
(ii) Your village/town/city, or any other place of your choice.
Ans: (i) A Tree
4-digit number examples:
Example - Number of leaves on a large tree
A mature tree could have thousands of leaves, especially in the case of large, leafy trees like banyan or oak. Example: A tree might have around 4,000-5,000 leaves.
5-digit number examples:
Example - The number of fruits or seeds produced by the tree in a year
Some trees, such as mango or apple trees, can produce thousands of fruits in a season. Example: A tree may produce around 10,000 fruits in a fruitful year.
(ii) Your Village / Town / City (or any place)
4-digit number examples:
Number of houses in a village = e.g., 1,500 houses
Number of school students in a small town = e.g., 4,200 students
5-digit number examples:
Population of a town = e.g., 75,000 people
Number of vehicles registered in a city = e.g., 48,000 vehicles
Total number of trees planted in a greening project = e.g., 20,000 trees
Pastime Mathematics
Sanju and Mira are traveling on a train. To pass time, they challenge each other with games and puzzles. Q1. Mira poses the river crossing puzzle to Sanju.
Q1. Mira poses the river crossing puzzle to Sanju.
A boatman wants to cross a river in a boat. He has to take a lion, a sheep, and a bundle of grass with him. He can take one of them at a time. If the sheep and grass are left on the shore, the sheep will eat the grass. And, if the sheep and lion are left on the shore, the lion will eat the sheep.
How can the boatman take the lion, sheep, and grass across the river?
Help him so that he can ferry the lion, sheep, and grass across the river safely, and in the minimum number of trips.
Ans: Trip 1: Take the sheep across the river. (Lion and grass left behind — safe)
Trip 2: Go back alone.
Trip 3: Take the lion across the river.
Trip 4: Bring the sheep back with you.
Trip 5: Take the grass across the river. (Leave the grass with lion — safe)
Trip 6: Go back alone.
Trip 7: Take the sheep across again.
Therefore, a total of 7 trips are required to ferry the lion, sheep, and grass across the river safely.
Q2. Sanju introduces a game called Pile of Pebbles to Mira.
There are two piles of pebbles. Each pile contains 7 pebbles. Each player can pick as many pebbles they want from either of the piles. The player who picks the last pebble wins.
Try this game with your friends. Now, how do you play so that you win?
To find a winning strategy, try playing with 1 pebble in each pile, two in each, three in each, and so on.
Ans: Keep both piles equal after your turn.
If they take from one pile, take the same number from the other.
When only 1 pebble is left in each pile, take one and win.
Example: If they take 3 from Pile A, you take 3 from Pile B.
Continue until you have taken the last pebble.
Q3. Now, it’s Mira’s turn. She gives a fun puzzle to Sanju with the following steps —
(a) Take any two different digits → 3 and 7
(b) Make two 2-digit numbers using them → 37 and 73
(c) Subtract the smaller number from the bigger number → 73 – 37 = 36
Now, use the two digits in the difference and repeat steps (b) and (c).
Continue this process until you get a 1-digit number. Even before everyone could finish, Mira exclaimed, “Mind you! No matter which two numbers you choose, you will get 9 in the end.”
The whole process will look as shown below. How did Mira know what the 1-digit number in the end would be? Let us explore.
How did Mira know what the 1-digit number in the end would be? Let us explore.
(1) Observe the differences you get in each step above. Do you notice anything in common?
Ans: All differences are multiples of 9 (36, 27, 45, 9) and their digits sum to 9.
36 → 3 + 6 = 9
27 → 2 + 7 = 9
45 → 4 + 5 = 9
9 → 9
(2) Try the puzzle using any other pair of digits. What is common to these differences? What do you get in the end?
Ans: Digits: 4 and 2
Numbers: 42 and 24 → 42 – 24 = 18
→ 1 and 8 → 81 – 18 = 63
→ 6 and 3 → 63 – 36 = 27
→ 7 and 2 → 72 – 27 = 45
→ 5 and 4 → 54 – 45 = 9
All differences are multiples of 9 (18, 63, 27, 45, 9) and have a digit sum of 9.
(3) What digits can you choose so that you get a 1-digit number in the first step itself? Give some examples. Describe the pattern in the digits.
Ans: Digits 4 and 3 → 43 – 34 = 9
Digits 2 and 1 → 21 – 12 = 9
Digits 5 and 4 → 54 – 45 = 9
Digits 6 and 5 → 65 – 56 = 9
So, digit pairs like (4, 3), (2, 1), (5, 4), and (6, 5) give a 1-digit number (9) in the first step itself.
(4) Now, find different digits such that the difference between the numbers is 27.
Ans: Try digits that differ by 3:
3 and 0 → 30 and 03 = 27
6 and 3 → 63 and 36 → 63 – 36 = 27
5 and 2 → 52 and 25 → 52 – 25 = 27
4 and 1 → 41 and 14 = 27
(5) Mira found an interesting relationship between the two digits and the difference obtained. Can you see it in the table that Mira made?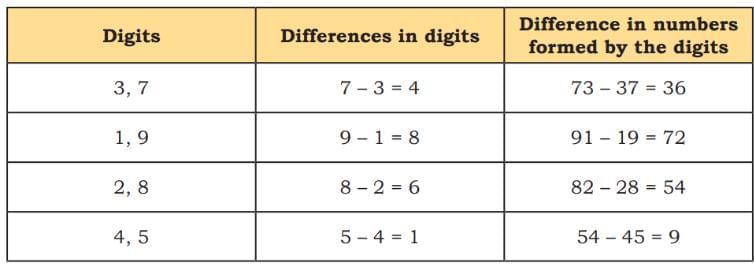 Ans: Difference in numbers formed by the digits = 9 × Difference in digits.
Ans: Difference in numbers formed by the digits = 9 × Difference in digits.
For example: 36 = 9 × 4
72 = 9 × 8
Q. Extend this table by choosing appropriate digits so that the resulting differences are 2, 3, 5, and 7 respectively.
Ans: 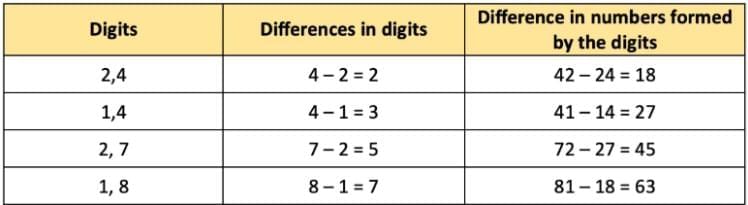 Q. What do the differences between the digits indicate?
Q. What do the differences between the digits indicate?
Ans: The greater the difference in digits, the greater the difference in numbers formed by the digits.
Q. List the numbers that give a 1-digit number in the third subtraction.
Ans: Example 1: Digits: 4, 1 → 41 – 14 = 27
→ digits: 2, 7 → 72 – 27 = 45
→ digits: 5, 4 → 54 – 45 = 9
Example 2: Digits: 3, 0 → 30 – 03 = 27
→ 7, 2 → 72 – 27 = 45
→ 5, 4 → 54 – 45 = 9
So, digit pairs like (4,1), (3,0), (2,7) give 1-digit number in the 3rd step.
Q. Identify pairs of digits that lead to the 1-digit number after the maximum possible number of subtractions. Compare your answers with your friends.
Ans: Digits with a large difference, e.g., 9 and 0:
90 – 09 = 81
→ 8,1 → 81 – 18 = 63
→ 6,3 → 63 – 36 = 27
→ 7,2 → 72 – 27 = 45
→ 5,4 → 54 – 45 = 9.
That’s 4 steps before reaching 9.
So, (9,0) or (8,1) lead to the longest chains
(Largest difference → biggest number → longer reduction chain)
Page 13 - 15
Let Us Do
Q1. Write 5 numbers between the numbers 23,568 and 24,234. ___________, ___________, ___________, ___________, and ___________
Ans: 23,678; 23,789; 23,894; 24,193 and 24,210.
Q2. Write 5 numbers that are more than 38,125 but less than 38,600. ___________, ___________, ___________, ___________, and ___________
Ans: 38,235; 38,346; 38,456; 38,482 and 38,575.
Q3. Ravi’s car has been driven for 56,987 km till now. Sheetal’s car has been driven 67,543 km. Whose car has been driven more? ________________.
Ans: 67,543 > 56,987.
Therefore, Sheetal’s car has been driven more.
Q4. The following are the prices of different electric bikes. Arrange the prices in ascending (increasing) order.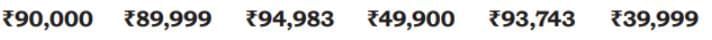 Ans: 39,999; 49,900; 89,999; 90,000; 93,743 and 94,983.
Ans: 39,999; 49,900; 89,999; 90,000; 93,743 and 94,983.
Q5. The following table shows the population of some towns. Arrange them in a descending (decreasing) order. __________ , __________ , __________ , __________ , __________, __________,
__________ , __________ , __________ , __________ , __________, __________,
Ans: 66,540 > 65,232 > 56,380 > 53,231 > 51,336 > 45,858.
So, Town 6 > Town 1 > Town 3 > Town 2 > Town 4 > Town 5.
Q6. Find numbers between 42,750 and 53,500 such that the ones, tens, and hundreds digits are all 0?
Ans: 43,000; 44,000; 45,000; 46,000; 47,000; 48,000; 49,000; 50,000; 51,000; 52,000; 53,000.
Q7. Write the following numbers in the expanded form. One has been done for you.
(a) 783 = 700 + 80 + 3
(b) 8,062 = _______________________________
(c) 9,980 = _______________________________
(d) 10,304 = _______________________________
(e) 23,004 = _______________________________
(f) 70,405 = _______________________________
Ans:
(b) 8,062 = 8000 + 60 + 2
(c) 9,980 = 9000 + 900 + 80
(d) 10,304 = 10,000 + 300 + 4
(e) 23,004 = 20,000 + 3,000 + 4
(f) 70,405 = 70,000 + 400 + 5
Q8. Fill in the blanks with the correct answer. Share your thoughts in class.
(a) 983 = 90 Tens + 83 Ones
(b) 68 = ___Tens + 18 Ones
(c) 607 = 4 Hundreds + ___Ones
(d) 5,621 = 4 Thousand + ___Hundreds + 2 Tens + ___Ones
(e) 7,069 = ___ Thousand + 20 Hundreds + ___ Ones
(f) 37,608 = ___Ten Thousand + 17 Thousand + ___Hundreds + 8 Ones
(g) 43,001 = 3 Ten Thousand + ____ Thousand + ____ Hundreds + 1 Ones
Ans: (b) 68 = 50 + 18
= 5 Tens + 18 Ones
(c) 607 = 400 + 207
= 4 Hundreds + 207 Ones
(d) 5,621 = 4000 + 1600 + 20 + 1
= 4 Thousand + 16 Hundreds + 2 Tens + 1 Ones (Answer may vary)
(e) 7,069 = 5000 + 2000 + 69
= 5 Thousand + 20 Hundreds + 69 Ones (Answer may vary)
(f) 37,608 = 20,000 + 17,000 + 600 + 8
= 2 Ten Thousand + 17 Thousand + 6 Hundreds + 8 Ones (Answer may vary)
(g) 43,001 = 30,000 + 10,000 + 3000 + 1
= 3 Ten Thousand + 10 Thousand + 30 Hundreds + 1 Ones (Answer may vary)
Q9. Fill in the blanks with the correct answers.
(a) How many notes of ₹10 are there in ₹7,934?
(b) How many notes of ₹100 are there in ₹7,934?
(c) How many thousands are there in 7,934?
(d) How many ₹500 notes are there in ₹7,934?
(Hint: Observe the answer of (iii))
(e) How many notes of ₹10 are there in ₹65,342?
(f) How many notes of ₹100 are there in ₹65,342?
(g) How many thousands are there in 65,342?
(h) How many ₹500 notes are there in ₹65,342?
Ans: (a) Number of notes of ₹10 in ₹7,934 = 7,934 ÷ 10 = 793
(b) Number of notes of ₹100 in ₹7,934 = 7,934 ÷ 100 = 79
(c) Number of thousands in ₹7,934 = 7,934 ÷ 1000 = 7
(d) Number of ₹500 notes in ₹7,934 = 7,934 ÷ 500 = 15
(e) Number of ₹10 notes in ₹65,342 = 65,342 ÷ 10 = 6534
(f) Number of ₹100 notes in ₹65,342 = 65,342 ÷ 100 = 653
(g) Number of thousands in ₹65,342 = 65,342 ÷ 1000 = 65
(h) Number of ₹500 notes in ₹65,342 = 65,342 ÷ 500 = 130
|
35 videos|248 docs|9 tests
|
FAQs on We are the Travellers NCERT Solutions - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are some effective strategies for teaching large numbers to fifth graders? |  |
| 2. How can parents support their children in learning mathematics at home? |  |
| 3. What role does problem-solving play in mathematics education for fifth graders? |  |
| 4. Why is it important for students to learn about large numbers and their applications? |  |
| 5. How can teachers incorporate fun activities to make mathematics engaging for students? |  |















