Important Formula: A Square and A Cube | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Square Number

if a natural number m can be expressed as n2, where n is also a natural number, then m is a square number.
Some Important point to Note
- All square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place
- if a number has 1 or 9 in the unit’s place, then it’s square ends in 1.
- when a square number ends in 6, the number whose square it is, will have either 4 or 6 in unit’s place
- None of square number with 2, 3, 7 or 8 at unit’s place.
- Even number square is even while odd number square is Odd
- there are 2n non perfect square numbers between the squares of the numbers n and (n + 1)
- if a natural number cannot be expressed as a sum of successive odd natural numbers starting with 1, then it is not a perfect square
How to find the square of Number easily
1. Identity method
We know that (a+b)2 =a2 +2ab+b2
Example: 232= (20+3)2 =400+9+120=529
2. Special Cases
(a5)2
= a(a + 1) hundred + 25
Example: 252=2(3) hundred + 25 = 625
Pythagorean triplets
For any natural number m > 1, we have (2m)2 + (m2 – 1)2 = (m2 + 1)2 So, 2m, m2 – 1 and m2 + 1 forms a Pythagorean triplet
Example: 6,8,10
62 +82 =102
Square Root
Square root of a number is the number whose square is given number
So we know that
m=n2 Square root of m
√m =n
Square root is denoted by expression √
How to Find Square root
1. Finding square root through repeated subtraction
We know sum of the first n odd natural numbers is n2. So in this method we subtract the odd number starting from 1 until we get the reminder as zero. The count of odd number will be the square root
Consider 36 Then,
(i) 36 – 1 = 35
(ii) 35 – 3 = 32
(iii) 32 – 5 = 27
(iv) 27 – 7 = 20
(v) 20 – 9 = 11
(vi)11 – 11 = 0
So 6 odd number, Square root is 6
2. Finding square root through prime Factorisation
This method, we find the prime factorization of the number. We will get same prime number occurring in pair for perfect square number. Square root will be given by multiplication of prime factor occurring in pair
Consider
81
81=(3×3)×(3×3)
√81= 3×3=9
Finding square root by division method
This can be well explained with the example
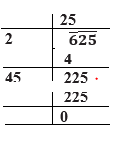
- Step 1: Place a bar over every pair of digits starting from the digit at one’s place. If the number of digits in it is odd, then the left-most single digit too will have a bar. So in the below example 6 and 25 will have separate bar.
- Step 2: Find the largest number whose square is less than or equal to the number under the extreme left bar. Take this number as the divisor and the quotient with the number under the extreme left bar as the dividend. Divide and get the remainder.
In the below example 4 < 6, So taking 2 as divisor and quotient and dividing, we get 2 as reminder - Step 3: Bring down the number under the next bar to the right of the remainder.
In the below example we bring 25 down with the reminder, so the number is 225 - Step 4: Double the quotient and enter it with a blank on its right.
In the below example, it will be 4 - Step 5: Guess a largest possible digit to fill the blank which will also become the new digit in the quotient, such that when the new divisor is multiplied to the new quotient the product is less than or equal to the dividend.
In this case 45 × 5 = 225 so we choose the new digit as 5. Get the remainder. - Step 6: Since the remainder is 0 and no digits are left in the given number, therefore the number on the top is square root
 In case of Decimal Number, we count the bar on the integer part in the same manner as we did above, but for the decimal part, we start pairing the digit from first decimal part.
In case of Decimal Number, we count the bar on the integer part in the same manner as we did above, but for the decimal part, we start pairing the digit from first decimal part.
Cube Number
Numbers obtained when a number is multiplied by itself three times are known as cube numbers
Example:
1=13
8=23
27=33
Some Important point to Note
- All cube numbers can end with any digit unlike square number when end with 0, 1, 4, 5, 6 or 9 at unit’s place
- if a number has 1 in the unit’s place, then it’s cube ends in 1.
- Even number cubes are even while odd number cubes are Odd
- There are only ten perfect cubes from 1 to 1000
- There are only four perfect cubes from 1 to 100
Prime Factorization of Cubes
When we perform the prime factorization of cubes number, we find one special property
8= 2×2×2 (Triplet of prime factor 2)
216 = (2 × 2 × 2) × (3 × 3 × 3) ( Triplet of 2 and 3)
Each prime factor of a number appears three times in the prime factorization of its cube.
Cube Root
Cube root of a number is the number whose cube is given number
So we know that 27=33
Cube root of 27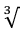 27 = 3
27 = 3
Cube root is denoted by expression 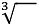
How to Find cube root
1. Finding cube root through prime factorization: This method, we find the prime factorization of the number. We will get same prime number occurring in triplet for perfect cube number. Cube root will be given by multiplication of prime factor occurring in pair
Consider 74088 = 2 × 2 × 2 × 3 × 3 × 3 × 7 × 7 × 7 = 23 × 33 × 73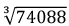 = 2 x 3 x 7 = 42
= 2 x 3 x 7 = 42
2. Finding cube root by estimation method: This can be well explained with the example The given number is 17576.
- Step 1: Form groups of three starting from the rightmost digit of 17576. 17 576. In this case one group i.e., 576 has three digits whereas 17 has only two digits.
- Step 2: Take 576. The digit 6 is at its one’s place. We take the one’s place of the required cube root as 6.
- Step 3: Take the other group, i.e., 17. Cube of 2 is 8 and cube of 3 is 27. 17 lies between 8 and 27. The smaller number among 2 and 3 is 2. The one’s place of 2 is 2 itself. Take 2 as ten’s place of the cube root of 17576.
- Thus,
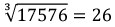
|
26 videos|133 docs|11 tests
|
FAQs on Important Formula: A Square and A Cube - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the easiest method to find the square of a number? |  |
| 2. What are Pythagorean triplets, and how can we find them? |  |
| 3. How can we calculate the square root of a number? |  |
| 4. What is the process to find the cube of a number? |  |
| 5. How can we find the cube root of a number? |  |
















