Important Formulas: A Story of Numbers | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Need to Count (Stone Age)
Purposes: Food, animals, trade, rituals, calendars.
No number names/symbols → Used one-to-one mapping with:
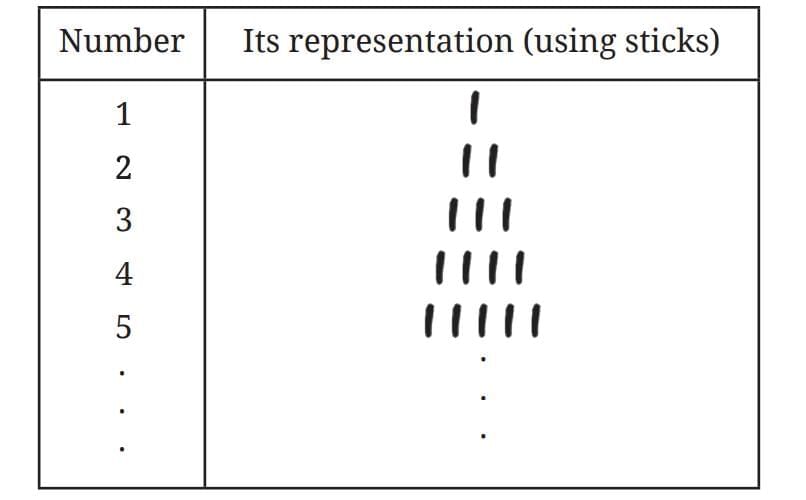
Sticks/Pebbles/Seeds (Method 1)
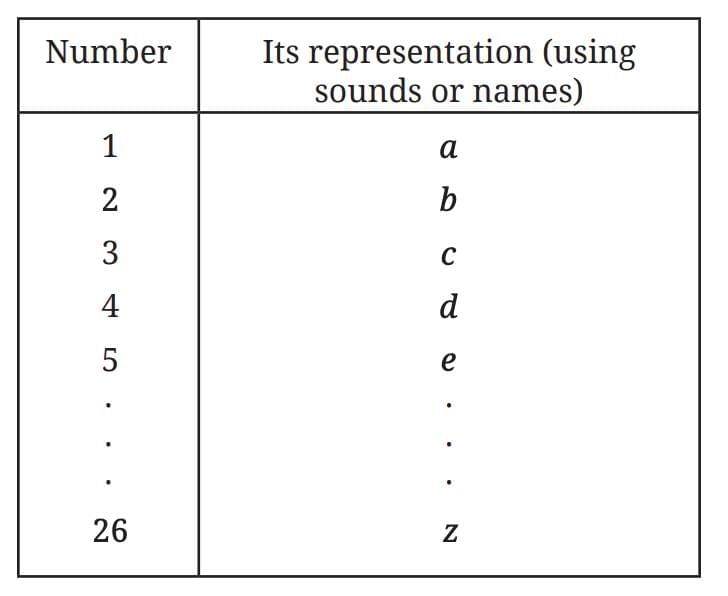
Sounds/Names (Method 2) → Limited by available sounds/letters.
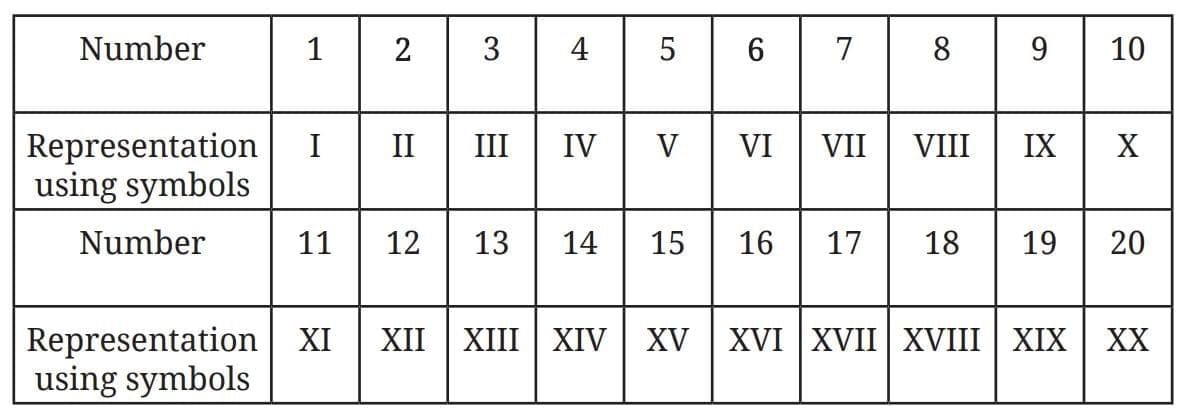
Written symbols (Method 3) → e.g., Roman numerals.
Key Concepts
One-to-One Mapping: Each object ↔ one counting unit.
Numerals = Written symbols in a number system.
Landmark Numbers: Special values to build other numbers (e.g., 1, 5, 10…).
Early Number Systems
(A)Tally Marks
Simple notches/lines.
Ishango Bone (20k–35k yrs old) – possibly calendar.
Lebombo Bone (44k yrs old) – lunar calendar.

(B) Counting in Groups
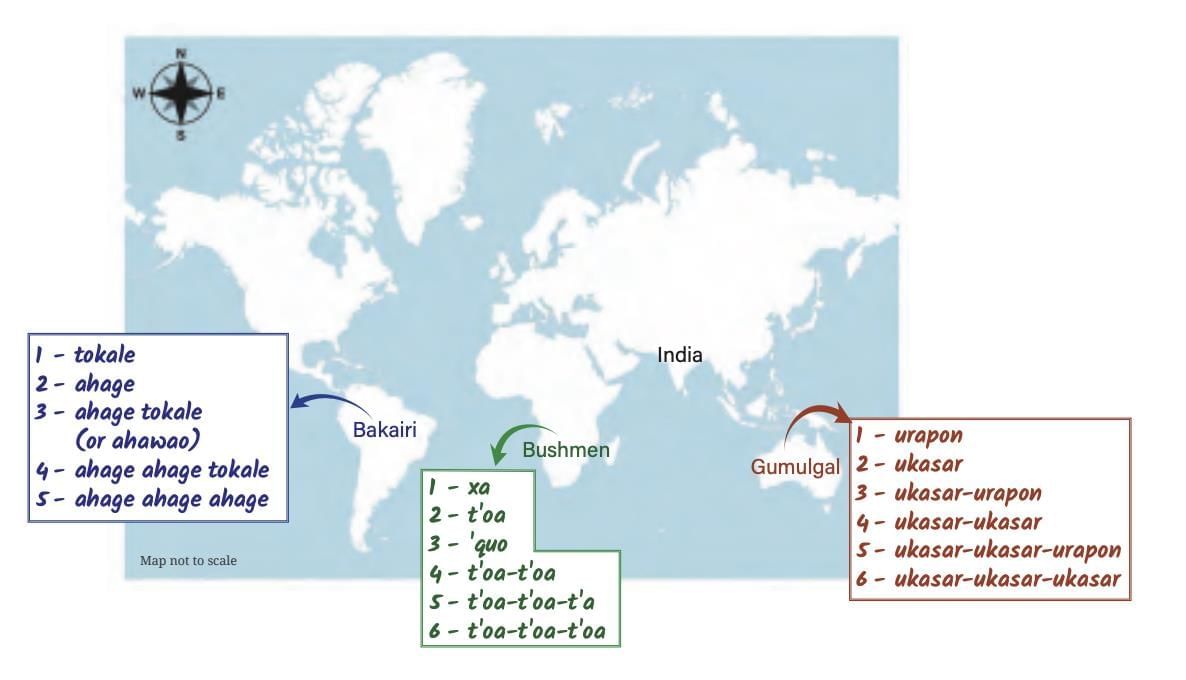
Gumulgal (Australia): Count in 2’s → Numbers = combinations of 2’s & 1’s.

Also used by Bakairi (S. America) & Bushmen (S. Africa).
Common groups in history: 2, 5, 10, 20.
(C) Roman Numerals
- Symbols:
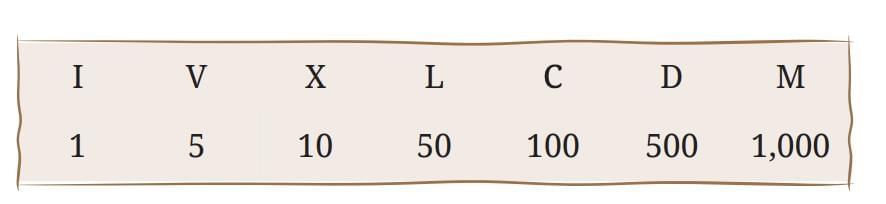
Rules:
If a smaller numeral is placed before a larger one, subtract it.
Example: IV = 5 − 1 = 4.If a smaller numeral is placed after a larger one, add it.
Example: VI = 5 + 1 = 6.
Advantage: Shorter than tally marks.
Limitations:
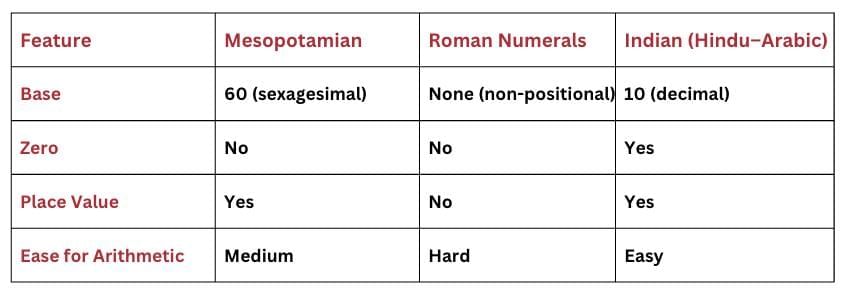
No zero.
Difficult for large numbers.
Cannot perform complex arithmetic easily.
Idea of Base-n
Base-n system: Landmark numbers = powers of n
Example: Base-5 → 1, 5, 25, 125…
Advantages: Consistent grouping, easier addition & multiplication.
Egyptian System
Base-10, symbols for 1, 10, 100, 1000, 10,000…
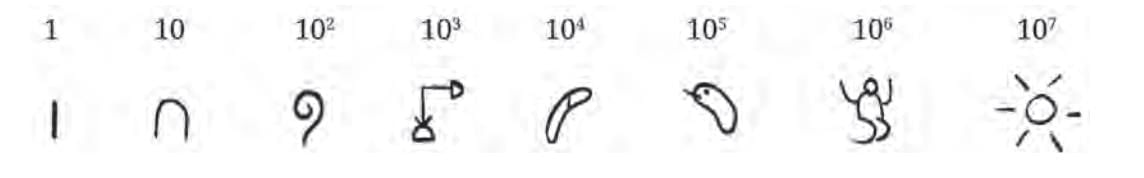
Build numbers by repeating symbols. For example 324 which equals 100 + 100 + 100 + 10 + 10 + 4 is written as

Limit: Needs infinite symbols for very large numbers.
Abacus
Decimal-based calculating tool.
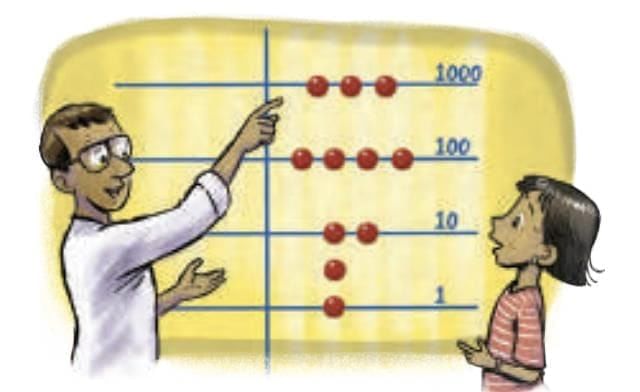
Each line = power of 10.
Counters above line = value of 5× that landmark.
Mesopotamian System
Location: Ancient civilisation in present-day Iraq and nearby regions.
Time Period: Around 4000 years ago.
Base: Base-60 (sexagesimal system).
Symbols:
Two main wedge-shaped symbols (cuneiform writing) for numbers.
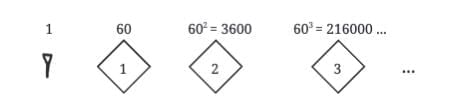
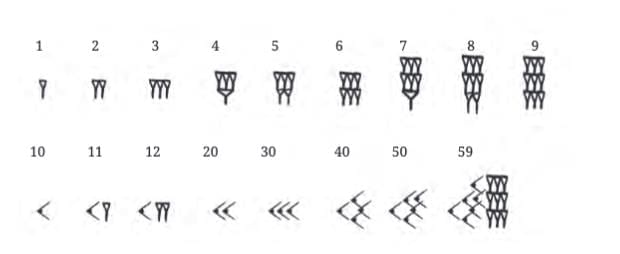
Numbers formed by repeating and combining these symbols.
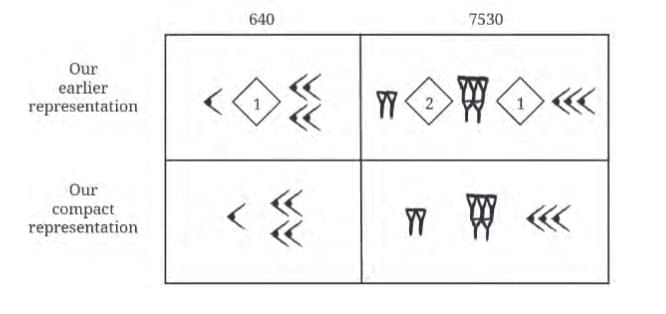
Special Use:
Still used today in measuring time (60 seconds in a minute, 60 minutes in an hour) and angles (360° circle).
Mayan Number System Basics
Base: Modified base-20.
1st place: 1’s (units)
2nd place: 20’s
3rd place: 360’s (not 400, due to calendar reasons)
4th place: 7200’s, etc.
Symbols:
Dot (•) = 1
Bar (—) = 5
Shell = 0 (placeholder)
Numbers are written vertically, lowest value at bottom.

Chinese Rod Numeral System – Key Points
1.
Purpose
Two systems existed:
Written system – for recording quantities.
Rod numeral system – for performing calculations efficiently.
2.
Rod Numerals
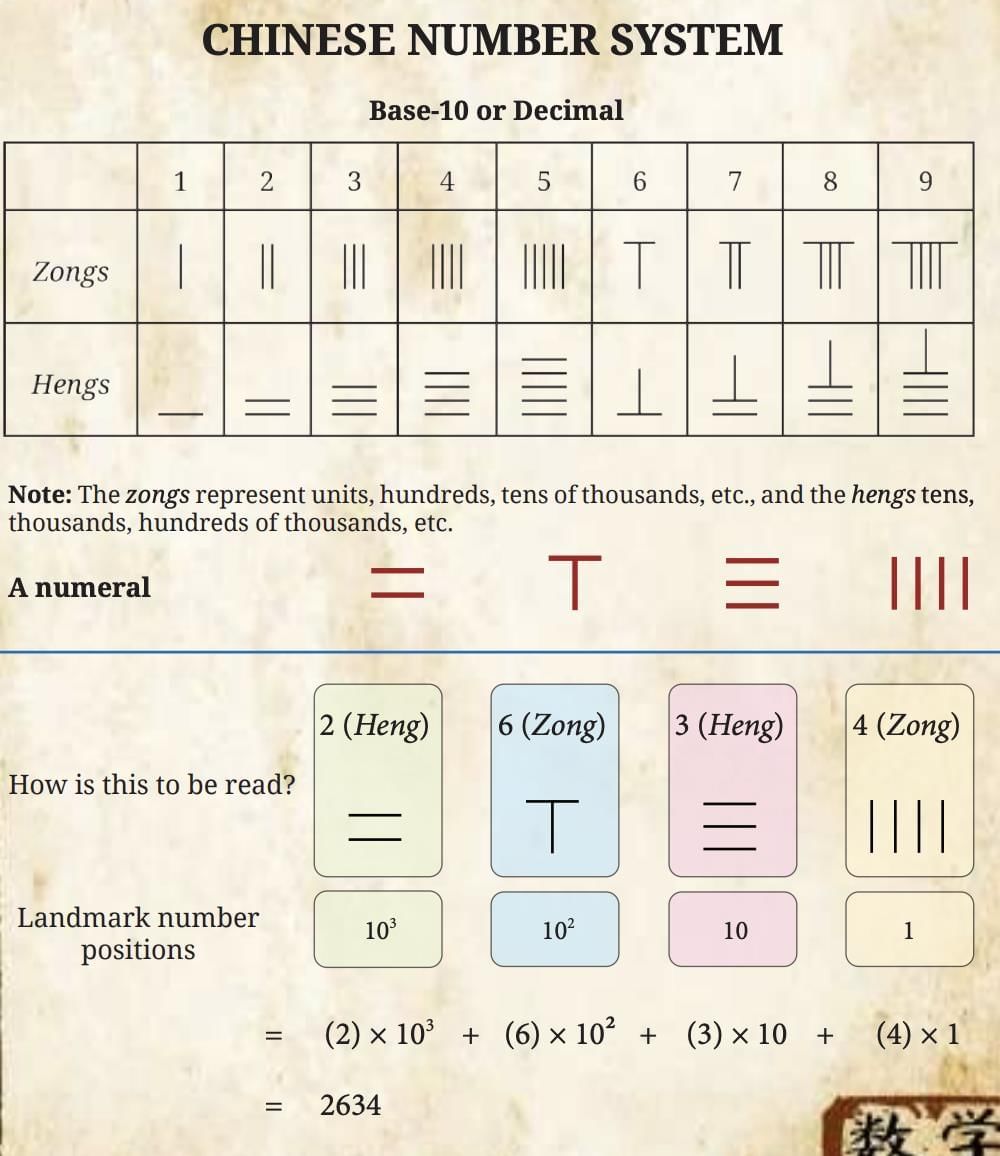
Base: Decimal (base-10), like our modern system.
Digits 1–9: Represented using vertical or horizontal rods (small sticks or lines).
Place value:
Vertical rods → used for units and hundreds places.
Horizontal rods → used for tens and thousands places.
(This alternation prevented confusion between adjacent digits.)
3.
Zero Representation
Like the Mesopotamians: used a blank space to indicate an empty place value.
Advantage: Due to uniform rod sizes, the blank space was easier to identify.
Note: If they had an actual symbol for zero, it would have been a fully developed place value system like the Hindu–Arabic numerals.
Spread of Hindu–Arabic Numerals

Base: Base-10 (decimal system).
Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Place Value System: Value of a digit depends on its position.
Example: In 375,
3 → Hundreds place = 3 × 100 = 300
7 → Tens place = 7 × 10 = 70
5 → Ones place = 5 × 1 = 5Use of Zero: A major contribution by Indian mathematicians (Aryabhata, Brahmagupta).
Spread: Carried to Europe by Arab traders → became the Hindu–Arabic numerals we use today.
Comparing Systems
|
26 videos|133 docs|11 tests
|
FAQs on Important Formulas: A Story of Numbers - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the key features of the Egyptian number system? |  |
| 2. How did the concept of base-n systems evolve in early number systems? |  |
| 3. What is the significance of the abacus in ancient number systems? |  |
| 4. Can you explain the basic principles of the Mayan number system? |  |
| 5. How did Hindu-Arabic numerals spread and become widely used? |  |

















