Sum of Consecutive Natural Numbers
Let four consecutive numbers be n, n + 1, n + 2, n + 3.
Their sum is n + (n + 1) + (n + 2) + (n + 3) = 4n + 6.
- – Example: For n = 7, the numbers are 7, 8, 9, 10, and their sum is 7 + 8 + 9 + 10 = 34.
To find four consecutive numbers with a given sum S:
- – 4n + 6 = S ⟹ n = (S – 6) / 4, where n must be an integer.
Example: If S = 34, then n = (34 – 6) / 4 = 7, so the numbers are 7, 8, 9, 10.
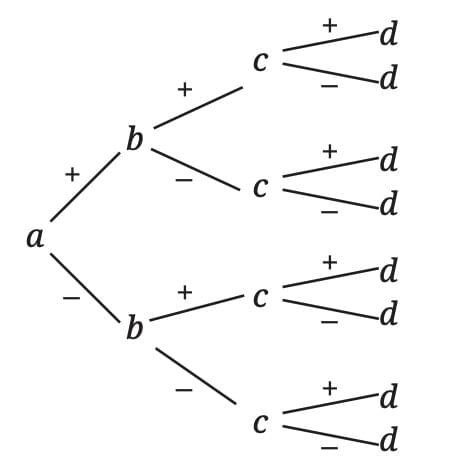
Four Consecutive Numbers with + and − Signs
Take four consecutive integers n, n+1, n+2, n+3. There are 8 possible expressions placing + or − between them.
All 8 expressions always have the same parity (either all even or all odd).
Basic Parity Rules (quick)
Even ± Even = Even
Odd ± Odd = Even
Odd ± Even = Odd
Even × any integer = Even
Odd × Odd = Odd
Expressions That Are Always Even
If every term is a multiple of 2, the whole expression is even.
Examples:
2a + 2b → always even
4m + 2n → always even
2u − 4v → always even
4k * 3j = 12kj → always even
Even Numbers vs. Multiples of 4
Even numbers are either multiples of 4 (remainder 0) or leave a remainder of 2 when divided by 4.
Cases for the sum of two even numbers:
- Both multiples of 4: 4p + 4q = 4(p + q), always a multiple of 4.
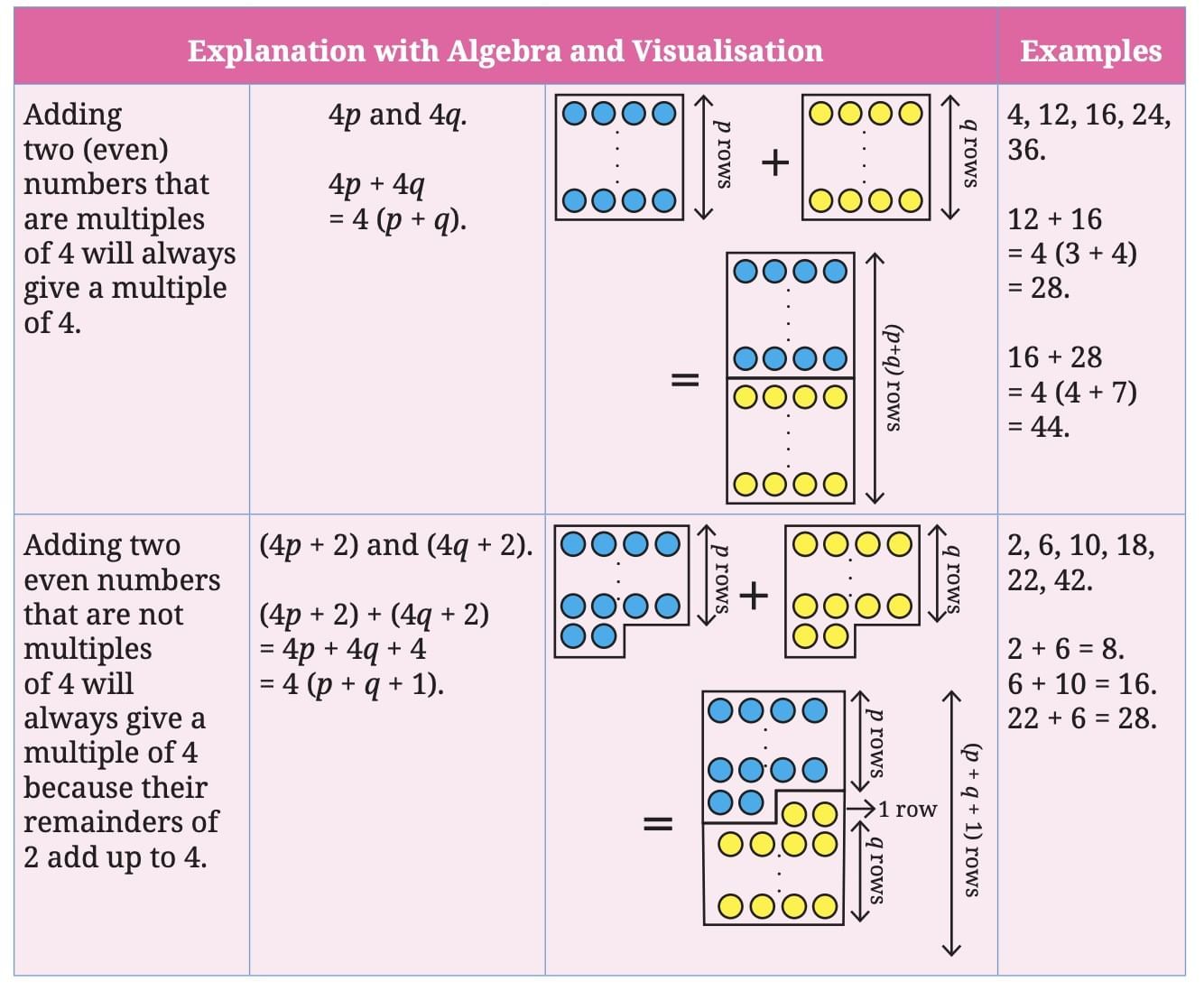
- Both not multiples of 4: (4p + 2) + (4q + 2) = 4p + 4q + 4 = 4(p + q + 1), always a multiple of 4.
- One multiple of 4, one not: 4p + (4q + 2) = 4(p + q) + 2, not a multiple of 4.
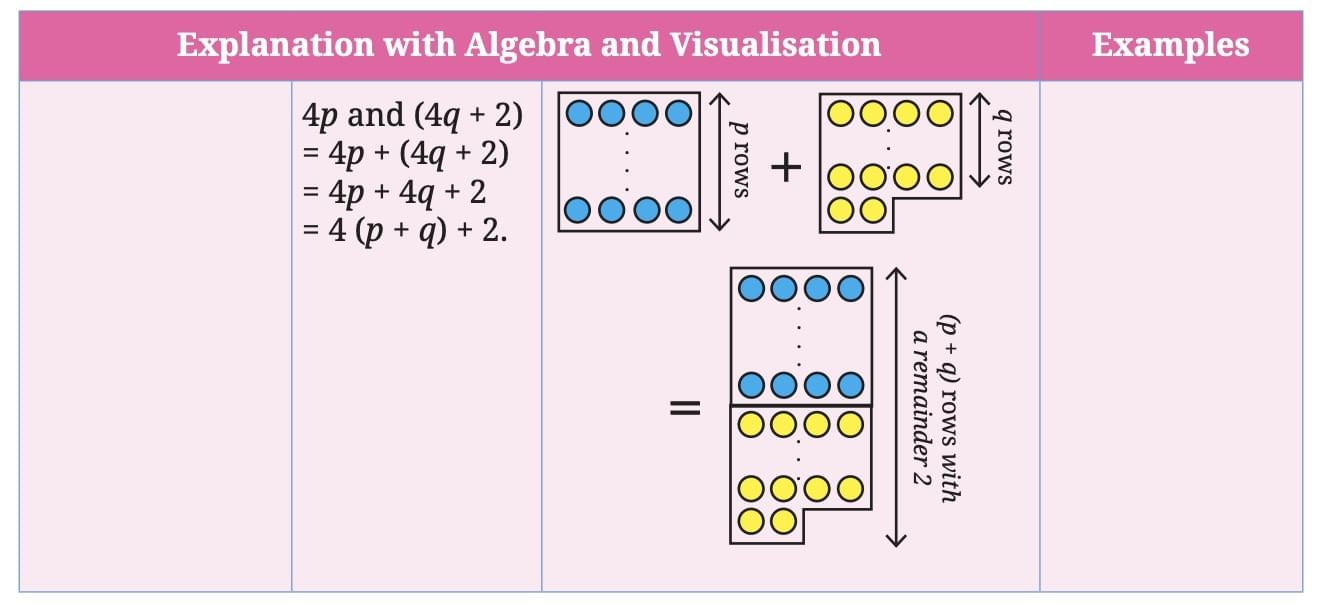
General rule: The sum of two even numbers is a multiple of 4 if both are multiples of 4 or both are not multiples of 4.
“Always / Sometimes / Never” Quick Facts about Divisibility
If 8 divides two numbers separately, then 8 divides their sum and difference. (Always true.)
If a number is divisible by both 9 and 4, it is divisible by 36 (LCM). (Always true.)
If a number is divisible by both 6 and 4, it is divisible by 24 (LCM). (Always true.)
If a number is divisible by 12, it is divisible by all factors of 12: 1,2,3,4,6,12. (Always true.)
If a number is divisible by 7, then any multiple of that number is also divisible by 7. (Always true.)
Odd + Even = multiple of 6 — Never true (odd + even is odd; multiples of 6 are even).
Numbers with a Given Remainder
Numbers with remainder 3 when divided by 5: 5k + 3.
- Example: k = 0, 1, 2, … , gives 3, 8, 13, 18, …
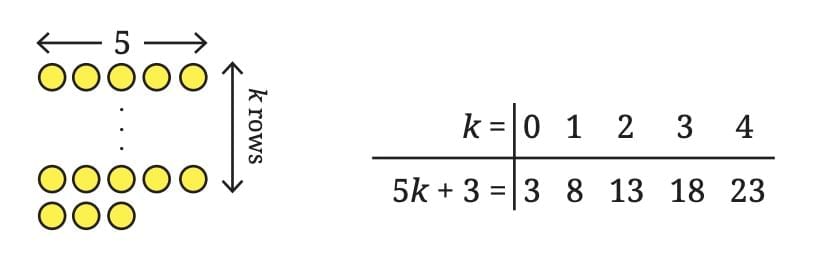
Numbers with remainder 2 when divided by 3 and 2 when divided by 4:
- General form: n = 12k + 2.
- Example: k = 0, 1, 2, … , gives 2, 14, 26, …
Quick Divisibility Rules
Divisible by 2: last digit is 0,2,4,6,8.
Divisible by 5: last digit is 0 or 5.
Divisible by 10: last digit is 0.
Divisible by 4: last two digits form a number divisible by 4.
Divisible by 8: last three digits form a number divisible by 8.
Divisible by 3: sum of digits divisible by 3.
Divisible by 9: sum of digits divisible by 9.
Divisible by 6: divisible by both 2 and 3.
Divisible by 24: divisible by both 3 and 8 (since 24 = 3 × 8 and gcd(3,8)=1).
Divisible by 11: (sum of digits in odd positions) − (sum of digits in even positions) is a multiple of 11.
Digital Roots
Definition: Sum digits repeatedly until a single digit remains.
Properties:
Digital root of a multiple of 9 is 9.
Digital root indicates divisibility by 3 or 9.
Examples:
489710: ( 4+8+9+7+1+0 = 29 ), ( 2+9 = 11 ), ( 1+1 = 2 ).
Multiples of 3: Digital roots cycle as 3, 6, 9.
Multiples of 6: Digital roots cycle as 6, 3, 9.
Parity Examples (quick checks)
43 + 37 = even (odd + odd = even)
672 − 348 = even (even − even = even)
4 × 347 × 3 = even (4 is even → product even)
708 − 477 = odd (even − odd = odd)
119 × 303 = odd (odd × odd = odd)
Cryptarithm Rules (letters-as-digits puzzles)
Each letter stands for one digit (0–9) and no two letters share the same digit.
Leading digit of a multi-digit number cannot be 0.
Use place-value reasoning and elimination to solve.






















