Remember:
- Write units for area (cm², m², km²).
- The area tells us the space inside a shape, not the length around it.
Preetha and Adrit’s grandmother made a quilt cover using old clothes. Now she wants to decorate it with lace, using two different colours. She decides to use two different coloured laces. How much lace of each kind will be needed to cover the entire border?

All these types of questions referring to the length around a plane figure are answered by ‘‘Perimeter’’.
The word perimeter is derived from two Greek words: peri, meaning around, and metron, meaning measure.
Thus, we measure the perimeter of a plane figure by adding the lengths of its sides.
Perimeter is the distance around a plane figure or the length of the boundary of a plane figure.
Observe the following example:
Remember:
- Write units for perimeter (cm, m, km).
- The perimeter tells us the length around and not about the inside.
A rectangle is a plane figure whose opposite sides (facing each other) are of equal lengths.
So, we have two equal lengths and two equal breadths.
Perimeter of a rectangle = length + breadth + length + breadth
= length + length + breadth + breadth
= 2 × length + 2 × breadth
= 2 × (length + breadth) = 2 × (l + b)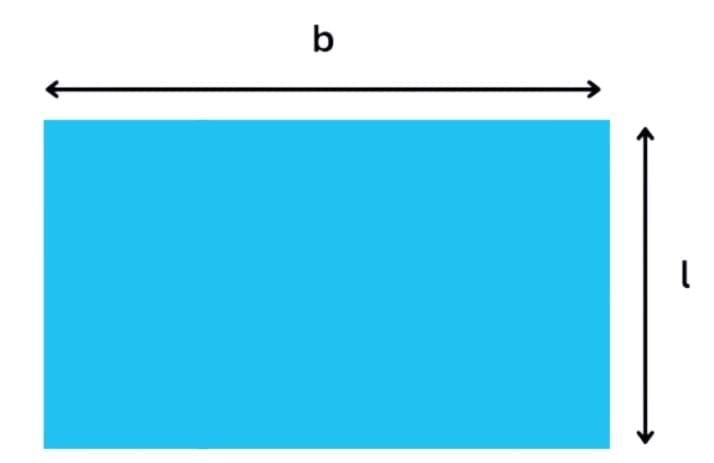
Perimeter of rectangle = 2 × (length + breadth)
A square is a plane figure whose all four sides are of equal lengths.
Perimeter of a square = side + side + side + side
= 4 × side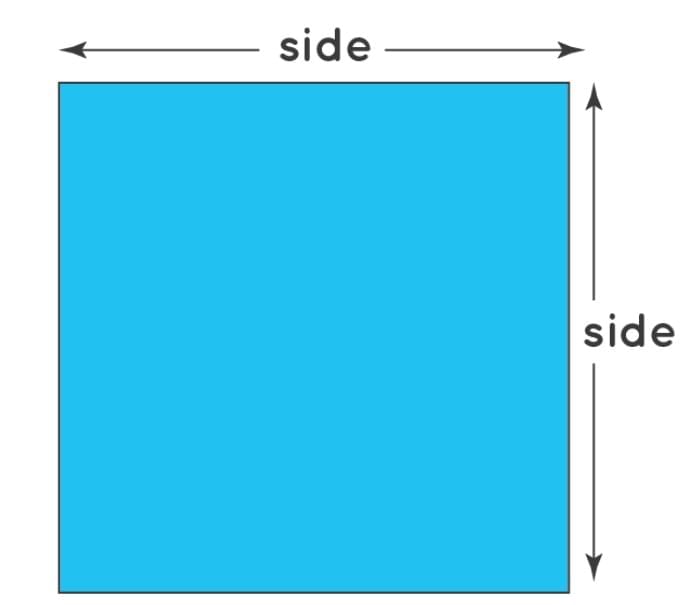
Perimeter of a square = 4 × length of one side
A triangle is a plane figure with three sides.
So, the perimeter of a triangle is the sum of the lengths of its three sides.
Perimeter of a triangle = A+ B+ C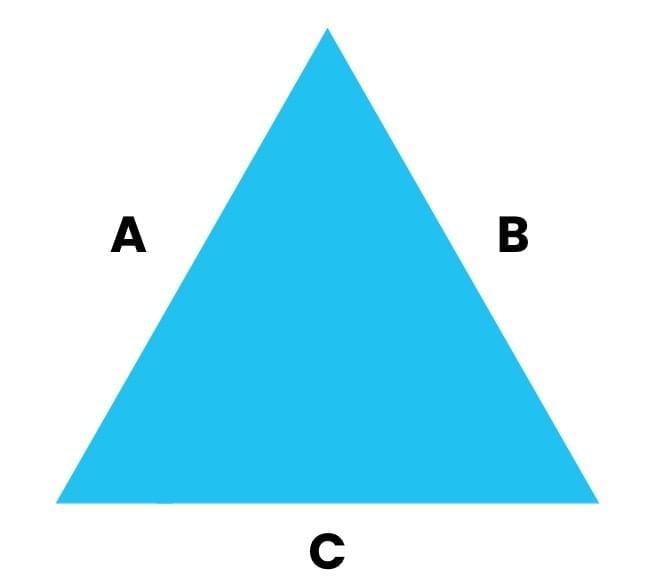
Perimeter of a triangle = side₁ + side₂ + side₃
Such a shape is where all sides are equal (like a regular polygon or regular hexagon).
To find its perimeter, we add the lengths of all the equal sides.
Perimeter = A + A + A + A + A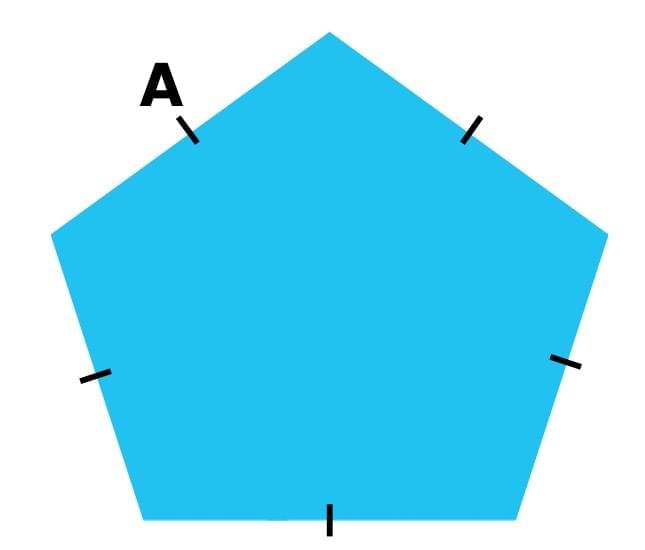
Perimeter = Number of sides × Length of one side
Now that we know how to measure the length around a shape, let’s think about how much space a shape covers inside.
Preetha and Adrit’s grandmother is making a rug with square patches. Look at the picture of the rug - can you count how many patches she has used? Each patch takes up some space, and all the patches together cover the whole rug.
Preetha and Adrit also tried covering their table using different shapes:

They found that triangle, square and rectangle shapes cover the top of the table without gaps and overlaps. Circle shape leaves gaps.
TWENTY triangles cover Table 1.
EIGHT squares cover Table 3.
SIX rectangles cover Table 4
You have been introduced to the concept of area in Class IV. Let us revise. How many marble tiles can fit on the floor or wall? How much paint is needed for the wall? All these questions refer to the surface within the boundary and are answered by Area.
The area of a shape is the amount of space it covers.
It refers to the flat surface taken by a plane figure. The region covered by the triangles, squares or rectangles is called the "area" of the table. To find the area of a region, we usually fill it with shapes that tile well — like squares, rectangles, and triangles. Circles do not tile perfectly because they leave spaces in between.
The units used to measure area are based on the units of length, i.e., mm, cm, m and km.
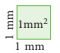 This is an area equal to 1 square millimetre (mm2).
This is an area equal to 1 square millimetre (mm2).
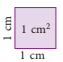 This is an area equal to 1 square centimetre (cm2).
This is an area equal to 1 square centimetre (cm2).
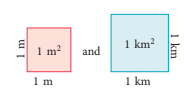 represent other units of measuring area ,such as 1 square metre (m2) and 1 square kilometre (km2).
represent other units of measuring area ,such as 1 square metre (m2) and 1 square kilometre (km2).
The unit used for measuring the area depends on the size of the area being measured.
For example, the areas of the following shapes are usually measured as under:

Remember:
- Write units for area (cm², m², km²).
- The area tells us the space inside a shape, not the length around it.
Steps to find the area using grids:
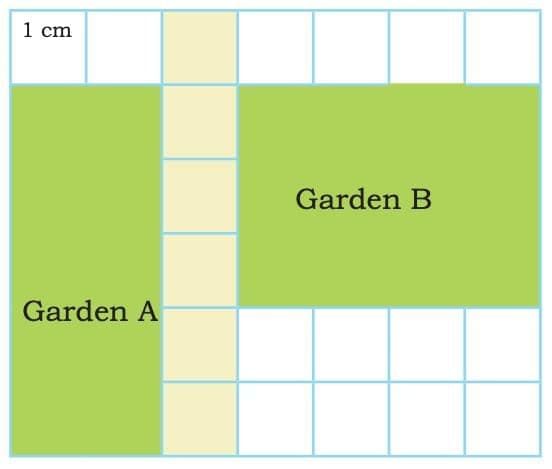
Area of Garden A = _____ cm square
Area of Garden B = _____ cm square
Sol: Area of Garden A = 10 cm²
Area of Garden B = 12 cm²Explanation:
Each small square in the grid is 1 cm².
When we count all the shaded squares in Garden A, we get 10.
When we count all the shaded squares in Garden B, we get 12.
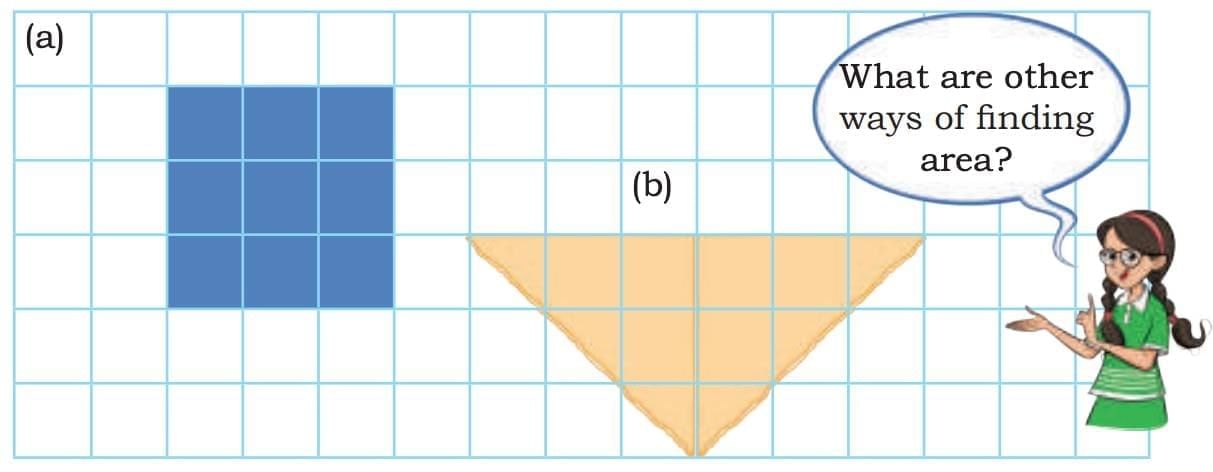
2. Is the area of shape (a) less than the area of shape (b) given below? Discuss.
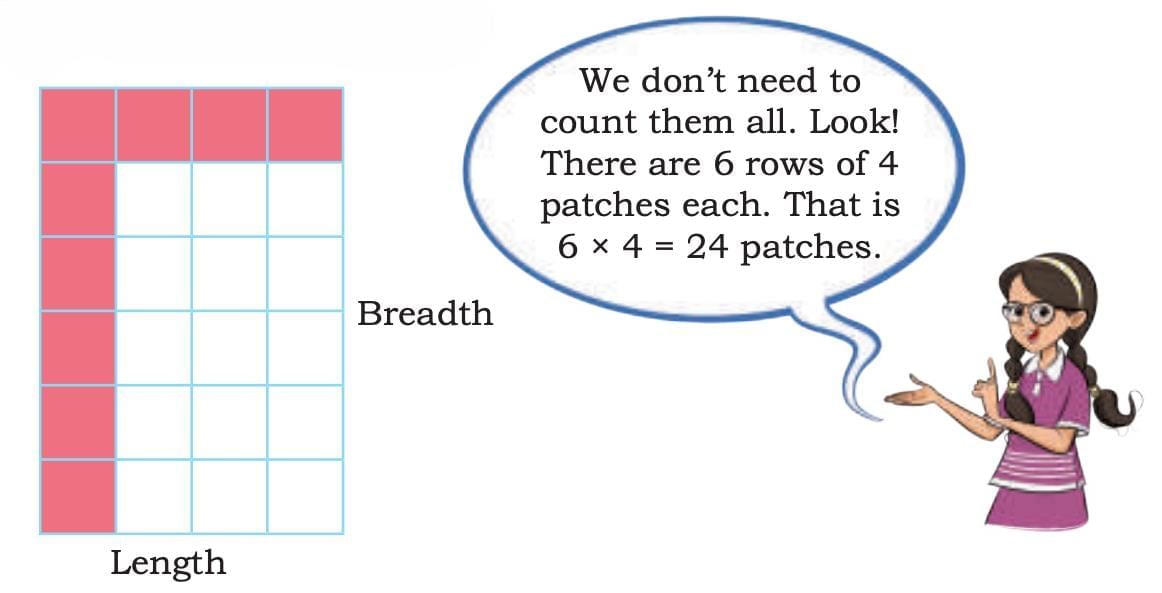
 Preetha and Adrit’s grandmother is making another square patchwork. She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?
Preetha and Adrit’s grandmother is making another square patchwork. She arranges the patches as shown below. Can you guess how many patches she will need? How did you find it?
Did you notice that 6 is the length of one side and 4 is the length of the non-equal side of the rectangle?
Sol: Yes, the area of shape (a) is less than the area of shape (b) because shape (b) covers more square units on the grid.
For the square patchwork, there are 6 rows with 4 patches in each row.
Total patches =
Here, 6 is the length and 4 is the breadth of the rectangle, showing that:Area of a Rectangle = Length × Breadth
Similarly, we can also find the perimeter of the rectangular shape.
Perimeter = Length + Length +Breadth + Breadth
= 2 × Length + 2 × Breadth
A rectangle is a plane figure whose opposite sides are equal.
So, it has two equal lengths and two equal breadths.
The area is the space covered inside the rectangle.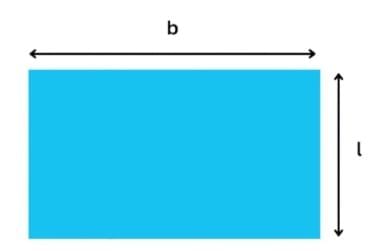
Area of a rectangle = length × breadth
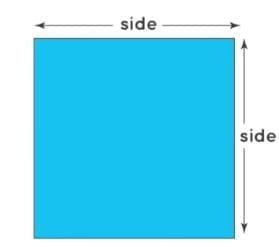
A square is a plane figure whose all four sides are equal.
The area is the space covered inside the square.
Area of a square = side × side = side²
Example:
1. Find the length of a rectangle if its area = 120 cm2 and its breadth = 10 cm
Sol: Area = 120 cm2, Breadth = 10 cm ∴ Length = Area ÷ Breadth = 120 cm2 ÷ 10 cm = 12 cm.
2. The perimeter of a square is 24 cm. Find its area.
Sol: To find the area, we need the side of the square.
Side of the square = Perimeter ÷ 4 = 24 cm ÷ 4 = 6 cm
∴ Area = side × side = 6 cm × 6 cm = 36 cm2.
|
35 videos|322 docs|7 tests
|
| 1. What is the difference between perimeter and area? |  |
| 2. How do you calculate the perimeter of a rectangle? |  |
| 3. What formula is used to find the area of a triangle? |  |
| 4. Why is it important to understand perimeter and area in everyday life? |  |
| 5. Can perimeter and area have the same value for certain shapes? |  |