Symmetrical Designs Chapter Notes | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
| Table of contents |

|
| Alphabet Cutout |

|
| Let Us Make a Windmill Firki |

|
| Let Us Do |

|
| Making Designs |

|
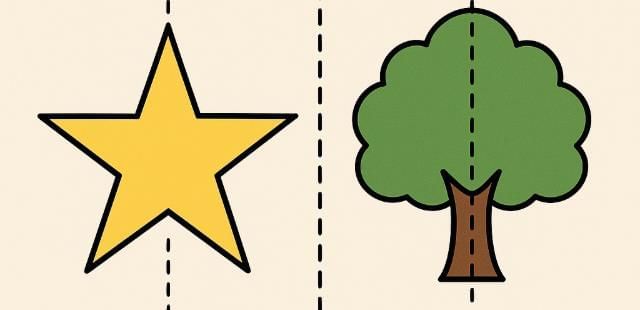
Symmetry means that when we divide a shape into two parts, both parts look the same, like a mirror image.
Alphabet Cutout
- Prem and Manu are making ‘Happy Birthday’ letter cutouts for Lali’s birthday.
- They notice that some letters can be divided into two halves very easily.
- This reminds them of what they learned in Grade 4 about reflection symmetry and lines of symmetry.
Let us recall:
Reflection Symmetry: A shape has reflection symmetry if one half is the mirror image of the other half. Imagine folding it along a line — both sides match exactly.
Line of Symmetry: The line that divides a shape into two equal, mirror-image halves is called the line of symmetry.
Vertical Line of Symmetry – The line goes up and down.
Horizontal Line of Symmetry – The line goes left to right.
Some shapes have more than one line of symmetry.
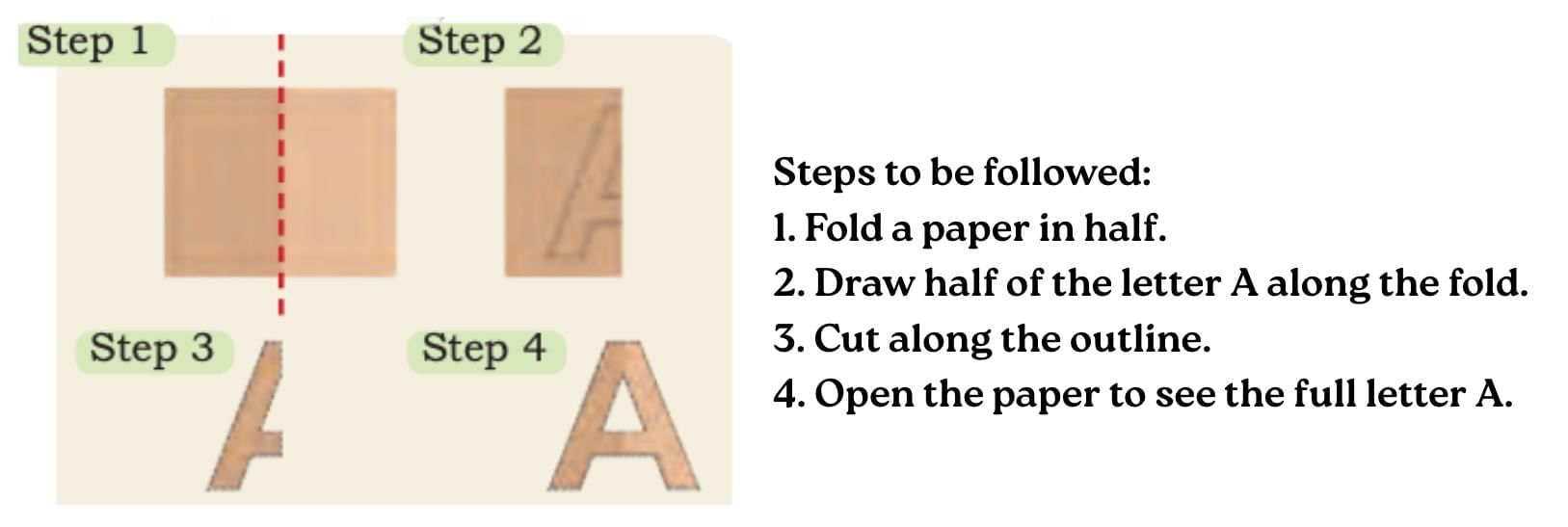
They used their knowledge of lines of symmetry to make the cutouts. The letter A has a vertical line of symmetry. So, to cut out the letter ‘A’:
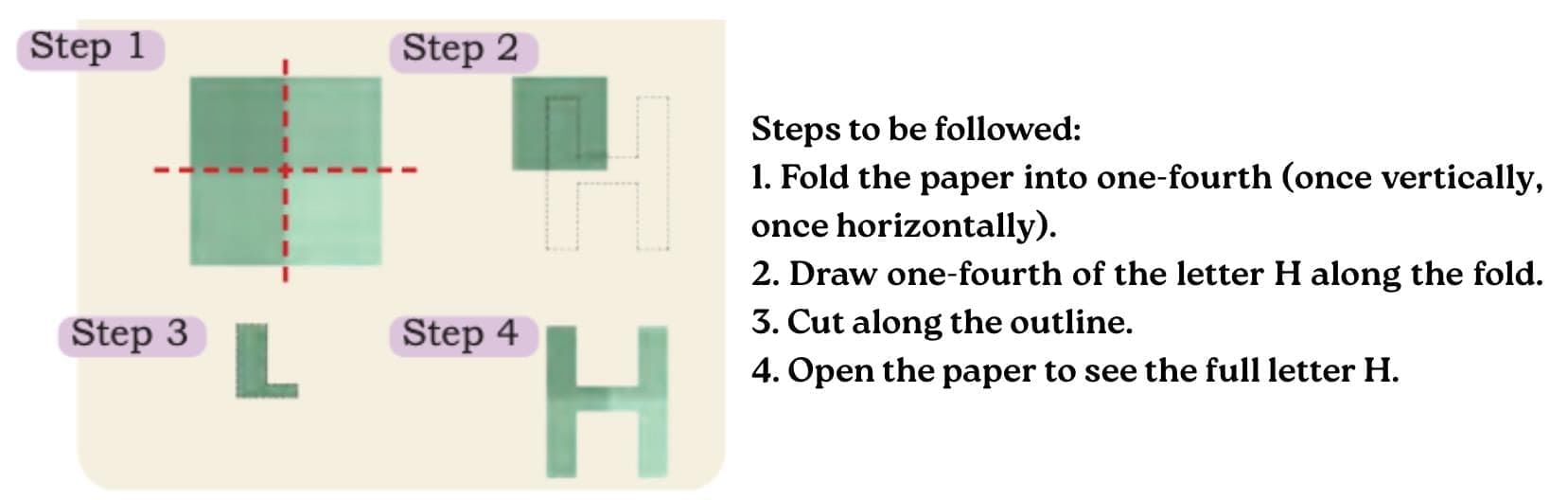
Similarly, for: The letter H has two lines of symmetry.
Alphabet Symmetry:
Which of the following alphabet cutouts can be made by just drawing half (1/2 ) or quarter (1/4 ) of the letter? You can do it by drawing lines of symmetry on the letters.

Which of the letters has a horizontal line of symmetry? _________________
Which of the letters has a vertical line of symmetry? ____________________
Which letters have both vertical and horizontal lines of symmetry?________
Sol: Letters that can be made by drawing half (1/2) or quarter (1/4) of the letter: E, X, T, O (because they have at least one line of symmetry to fold along)
Letters with a horizontal line of symmetry: E, X, O
Letters with a vertical line of symmetry: X, T, O, V
Letters with both vertical and horizontal lines of symmetry: X, O
So far, we have seen shapes that can be divided into equal mirror-image halves using lines of symmetry. But what if instead of folding them, we turn them? This brings us to our next concept, known as the Rotational Symmetry.
Rotational Symmetry
Meaning
A shape has rotational symmetry if it looks the same even after we turn it around its centre.
(The turn is less than one full round).
Order of Rotational Symmetry
- It tells us how many times a shape looks the same in one full turn (360°).
- Example: A square matches itself 4 times in one full turn, so its order of rotational symmetry is 4.
Let Us Make a Windmill Firki
To see rotational symmetry in action, let’s make a windmill firki! When the firki spins around its centre, its blades look the same in many positions during one full turn.
Lali makes firkis for her friends. Follow the steps given below to make your firki:
1. Take a square paper.
2. Fold the paper in half diagonally to make two triangles.
3. Open and fold it the other way to make two more triangles.
4. Open it again. You will see an ‘X’ shape on the paper.
5. Use scissors to cut along the four lines of the ‘X’. Stop cutting about halfway to the centre.
6. Take one corner of each triangle and fold it gently towards the centre of the paper. Do not press it flat.
7. Fold every other corner towards the centre.
8. Push a pin through the folded corners and the centre of the paper.
9. Push the pin through a stick or straw
Observe the dot in the firki. Does the firki look the same after 1/4, 1/2, 3/4, and a full turn?
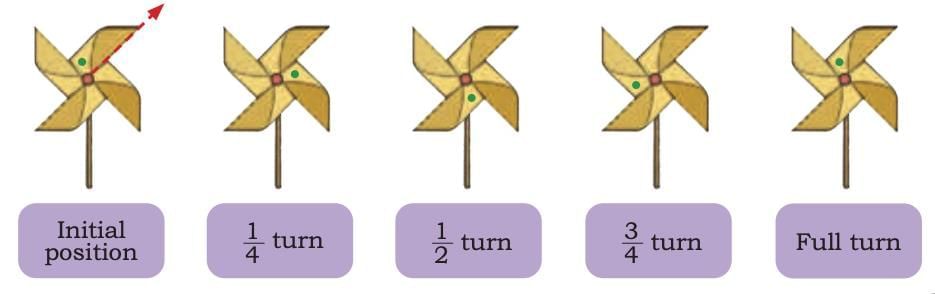
Sol: Yes, the firki looks the same after 1/4, 1/2, 3/4, and a full turn because it has rotational symmetry of order 4.
Let Us Do
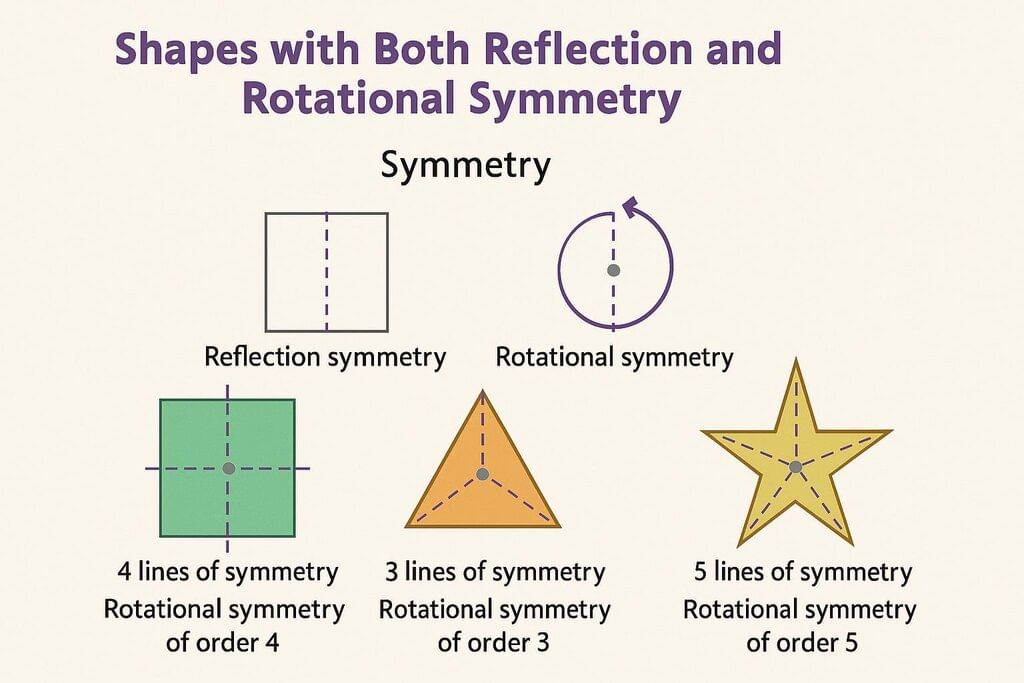
Shapes with Both Reflection and Rotational Symmetry
- We have learned about reflection symmetry (folding to get mirror images) and rotational symmetry (turning to get the same shape).
- Some shapes have both kinds of symmetry.
- Example: A square
- It can be folded along 4 different lines of symmetry.
- It also looks the same 4 times in one full turn (order of rotational symmetry = 4).
Find symmetry in the digits:

Which digit(s) have reflection symmetry? ___________________________
Which digit(s) have rotational symmetry? ___________________________
Which digit(s) have both rotational and reflection symmetries? ________
Now, let us look at the following numbers: ||, |00|
Do these have (a) rotational symmetry, (b) reflection symmetry or (c) both symmetries?
Give examples of 2-, 3-, and 4-digit numbers which have rotational symmetry, reflection symmetry, or both.
Sol:
Which digit(s) have reflection symmetry?
0, 1, 8
Which digit(s) have rotational symmetry?
0, 1, 8
Which digit(s) have both rotational and reflection symmetries?
0, 1, 8For || and |00|: Both have both symmetries. Examples:
- Rotational symmetry:
2-digit → 69, 11, 88
3-digit → 101, 609, 818
4-digit → 1001, 1881- Reflection symmetry:
2-digit → 11, 88
3-digit → 181, 101
4-digit → 1001, 8008- Both symmetries:
2-digit → 11, 88
3-digit → 101, 808
4-digit → 1001, 1881
Making Designs
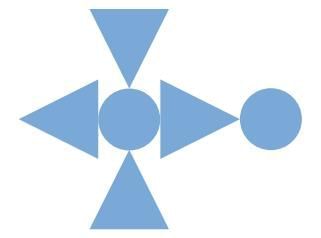
(a) Does the design have rotational symmetry? Yes/No.
(b) Try to change the design by adding some shape(s) so that the new design looks the same after a 12 turn. Draw the new design in your notebook.
(c) Now try to modify or add more shapes so that the new design looks the same after 14 turns. Draw the new design in your notebook.
(d) Do the new designs have reflection symmetry? If yes, draw the lines of symmetry
Sol:
(a) No. The design does not look the same after turning it ½ turn (180°) or ¼ turn (90°) because the right side has an extra circle that breaks the balance.
(b) Add another identical circle on the left side, opposite to the existing one. Now the design will look the same after a ½ turn.
(c) To get ¼ turn symmetry, you will need to place identical shapes in all four directions (top, bottom, left, and right) so that after turning 90°, the design remains unchanged. This means adding circles and triangles in the missing positions.
(d) 1. The modified design with ½ turn symmetry will have one vertical line of symmetry.
2. The modified design with ¼ turn symmetry will have two lines of symmetry — vertical and horizontal (and possibly diagonal if shapes are perfectly aligned).
|
35 videos|322 docs|7 tests
|
FAQs on Symmetrical Designs Chapter Notes - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What is symmetry, and why is it important in design? |  |
| 2. What is rotational symmetry? |  |
| 3. Can you give examples of shapes that have both reflection and rotational symmetry? |  |
| 4. How can symmetry be found in nature? |  |
| 5. How do artists and architects use symmetry in their work? |  |
















