Word Problems: A Square and A Cube | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1: Is 176 a perfect square? If not, find the smallest number by which it should be multiplied to get a perfect square.
Solution: Prime factorization of 176:
176 = 2⁴ × 11.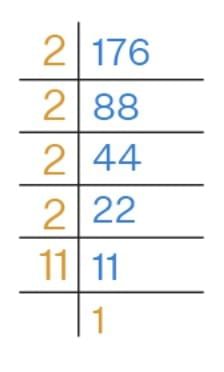 To make it a perfect square, multiply by 11.
To make it a perfect square, multiply by 11.
176 × 11 = 1936, which is a perfect square.
√1936 = 44.
Q2: Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.
Solution: Prime factorization of 9720:
9720 = 23 × 35 × 5 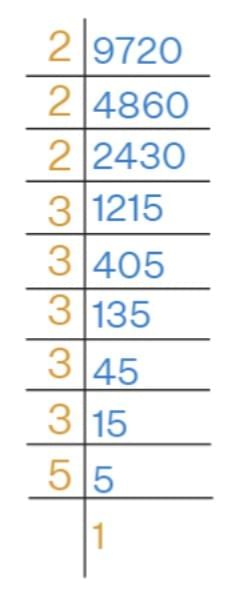 To make it a perfect cube, divide by 32 × 5 = 45
To make it a perfect cube, divide by 32 × 5 = 45
Divide 9720 by 21725 to get a perfect cube.
Q3: By what smallest number should 216 be divided so that the quotient is a perfect square? Also, find the square root of the quotient.
Solution:
Prime factorization of 216:
216 = 2³ × 3³.
To make the quotient a perfect square, divide by 2 and 3.
216 ÷ 6 = 36
√36 = 6
Q4: By what smallest number should 3600 be multiplied so that the quotient is a perfect cube? Also, find the cube root of the quotient.
Solution:
Prime factorization of 3600:
3600 = 2⁴ × 3² × 5².
To make it a perfect cube, multiply by 2² × 3 × 5 = 4 × 3 × 5 = 60.
3600 × 60 = 216000, and the cube root of 216000 is 60.
Q5: A farmer wants to plough his square field of side 150m. How much area will he have to plough?
Solution:
The area of a square field is given by the formula:
Area = (side)2
Here, the side of the square field is 150 meters.
Area = (150)2 = 22,500 m²
So, the farmer will have to plough 22,500 square meters.
Q6: What will be the number of unit squares on each side of a square graph paper if the total number of unit squares is 256?
Solution:
The total number of unit squares on a square graph paper is the square of the number of unit squares on each side.
Let the number of unit squares on each side be x.
So, x² = 256.
Taking the square root of both sides:
x = √256 = 16
Therefore, there are 16 unit squares on each side of the square graph paper.
Q7: If one side of a cube is 15m in length, find its volume.
Solution:
The volume of a cube is given by the formula:
Volume = side³
Here, the side length is 15 meters.
Volume = 15³ = 3375 m³
So, the volume of the cube is 3375 cubic meters.
Q8: Find the number of plants in each row if 1024 plants are arranged so that the number of plants in a row is the same as the number of rows.
Solution:
The total number of plants is 1024, and we are told that the number of plants in each row is the same as the number of rows.
Let the number of rows (and plants per row) be x.
The total number of plants is the product of the number of rows and the number of plants per row:
x × x = 1024
x² = 1024
Taking the square root of both sides:
x = √1024 = 32.
Therefore, the number of plants in each row is 32.
Q11: Difference of two perfect cubes is 189. If the cube root of the smaller of the two numbers is 3, find the cube root of the larger number.
Solution:
Let the two perfect cubes be x³ and y³, where x is the cube root of the smaller number and y is the cube root of the larger number.
We are given:
y³ - x³ = 189 and x = 3.
So, 3³ = 27.
Now, substitute into the equation:
y³ - 27 = 189
y³ = 189 + 27 = 216
So, y = ∛216 = 6.
Therefore, the cube root of the larger number is 6.
Q10: A hall has a capacity of 2704 seats. If the number of rows is equal to the number of seats in each row, then find the number of seats in each row.
Solution:
Let the number of rows and the number of seats in each row be x.
The total number of seats is given by:
x × x = 2704
x² = 2704
Taking the square root of both sides:
x = √2704 = 52.
Therefore, the number of seats in each row is 52.
|
22 videos|133 docs|11 tests
|
FAQs on Word Problems: A Square and A Cube - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the difference between a square and a cube in terms of geometry? |  |
| 2. How can I calculate the area of a square? |  |
| 3. How do you find the volume of a cube? |  |
| 4. What are some real-life examples of squares and cubes? |  |
| 5. Why is understanding squares and cubes important in mathematics? |  |

















