Unit Test (Solutions): A Square And A Cube | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question numbers 12 & 13 carry 5 marks each
Q1: Which of the following is NOT a possible units digit of a perfect square? (1 Mark)
a) 1
b) 4
c) 7
d) 9
Answer: c) 7
Perfect squares can only have units digits 0, 1, 4, 5, 6, 9.
So 7 is not possible.
Q2: How many perfect squares are there between 1 and 100 (inclusive)? (1 Mark)
a) 9
b) 10
c) 11
d) 12
Answer: b) 10
Perfect squares between 1 and 100 are:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 → 10 numbers.
Q3: Which of the following numbers is the smallest Taxicab Number? (1 Mark)
a) 4104
b) 13832
c) 1729
d) 1000
Answer: c) 1729
1729 is the smallest Taxicab number.
It is the smallest number expressible as the sum of two cubes in two different ways:
1729 = 1³ + 12³ = 9³ + 10³.
Q4: In prime factorisation, a number is a perfect square if: (1 Mark)
a) All prime factors occur in odd powers
b) All prime factors occur in even powers
c) It has more than 2 prime factors
d) It is greater than 100
Answer: b) All prime factors occur in even powers
A number is a perfect square if all prime factors occur in even powers.
Example: 144 = 2⁴ × 3² → both exponents are even.
Q5: The cube of 10 can be expressed as the sum of: (1 Mark)
a) 10 consecutive odd numbers
b) 10 consecutive even numbers
c) 20 consecutive odd numbers
d) 5 consecutive odd numbers
Answer: a) 10 consecutive odd numbers
The cube of a number n can be written as the sum of n consecutive odd numbers.
10³ = 1000 = 91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109 → 10 consecutive odd numbers.
Q6: A square park has an area of 6400 m². Find the length of one side. (2 Marks)
Solution: Side = √(area)
= √6400
= 80 m
Q7: If x² = 2116, find x. (2 Marks)
Solution: √2116 = 46,
so x = ±46
x = 46 or x = −46
Q8: A cube has a volume of 2197 cm³. Find the length of one edge. (2 Marks)
Solution:
Edge = ³√2197; 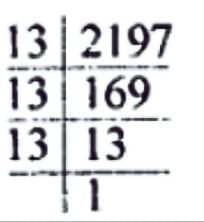 since 13³ = 2197,
since 13³ = 2197,
edge = 13 cm
Q9: Find the least number that must be subtracted from 1200 to make it a perfect square. Also, find that perfect square. (3 Marks)
Solution:
342=1156, 352=1225.
Nearest lower square .
Subtract .
Q10: Find the least number by which 1323 must be divided so that the quotient is a perfect cube. Also, find the cube root of the quotient. (3 Marks)
Solution:
Prime factorise 1323:
1323 ÷ 3 = 441 = 3² × 7² ⇒ 1323 = 3³ × 7²
For a perfect cube, each prime’s power must be a multiple of 3.
Remove the extra 7² by dividing by 7² = 49.
Quotient = 1323 ÷ 49 = 27 = 3³
Cube root of the quotient = ∛27 = 3.
⇒ Divide by 49; the quotient is 27, and its cube root is 3.
Q11: A square garden has an area of 3136 m². If the length and width are equal, find the length of one side of the garden. (3 Marks)
Solution:
Let the length of one side be x.
Area of garden:
x × x = 3136
x² = 3136
Taking the square root of both sides:
x = √3136 = 56
Therefore, the length of one side of the garden is 56 m.
Q12: The Difference of two perfect cubes is 189. If the cube root of the smaller of the two numbers is 3, find the cube root of the larger number. (5 Marks)
Solution:
Let the two perfect cubes be x³ and y³, where x is the cube root of the smaller number and y is the cube root of the larger number.
We are given:
y³ - x³ = 189 and x = 3.
So, 3³ = 27.
Now, substitute into the equation:
y³ - 27 = 189
y³ = 189 + 27 = 216
So, y = ∛216 = 6.
Therefore, the cube root of the larger number is 6.
Q13: Find the number of plants in each row if 1024 plants are arranged so that the number of plants in a row is the same as the number of rows. (5 Marks)
Solution:
The total number of plants is 1024, and we are told that the number of plants in each row is the same as the number of rows.
Let the number of rows (and plants per row) be x.
The total number of plants is the product of the number of rows and the number of plants per row:
x × x = 1024
x² = 1024
Taking the square root of both sides:
x = √1024 = 32.
Therefore, the number of plants in each row is 32.
|
26 videos|133 docs|11 tests
|
FAQs on Unit Test (Solutions): A Square And A Cube - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the difference between a square and a cube? |  |
| 2. How are the area and volume of a square and a cube calculated? |  |
| 3. Can you give examples of real-life objects that are squares and cubes? |  |
| 4. What are some practical applications of squares and cubes in mathematics? |  |
| 5. How can I improve my understanding of squares and cubes for exams? |  |





















