Daljeet Kaur runs a milk processing unit. Her dairy is full of milk, butter, and ghee packets. Every day, she needs to arrange items in groups, count them quickly, and calculate totals. Can you imagine doing this one by one? That’s why multiplication is so helpful!
Can you imagine doing this one by one? That’s why multiplication is so helpful!
What is Multiplication?
Multiplication means making equal groups.
- Example: 6 × 2 means 6 groups of 2.
- It is the same as repeated addition (2 + 2 + 2 + 2 + 2 + 2).
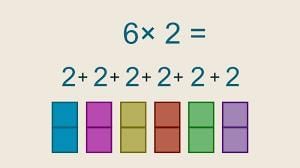
Now, let us help Daljeet Kaur in the calculation.
1. Daljeet Kaur sells 6 packets of butter every day. She wants to know how many packets she sells in 7 days (one week).
If she adds one by one, it looks like this:
6 + 6 + 6 + 6 + 6 + 6 + 6 = 42
Using multiplication, she can write it quickly as:
7 × 6 = 42
So, Daljeet sells 42 packets of butter in one week.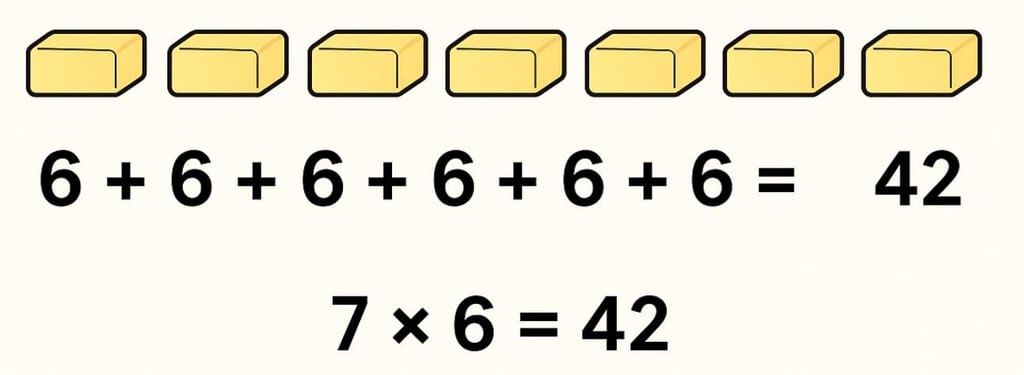 Here we see that multiplication is a faster and easier way to find the total than adding again and again.
Here we see that multiplication is a faster and easier way to find the total than adding again and again.
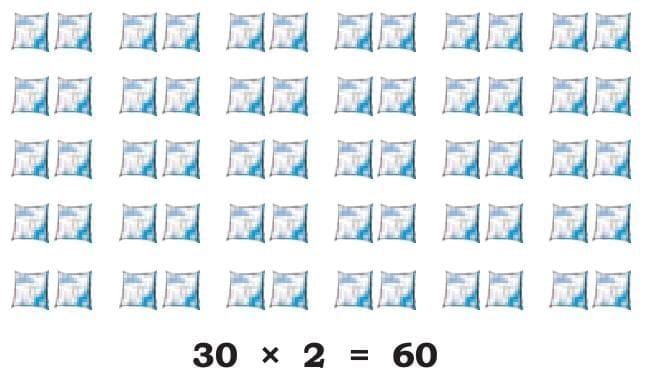
2. One day, Daljeet packed 60 butter milk pouches to sell. She wanted to arrange them in equal groups. She tried different ways:
She made 30 groups of 2 → 30 × 2 = 60
She made 20 groups of 3 → 20 × 3 = 60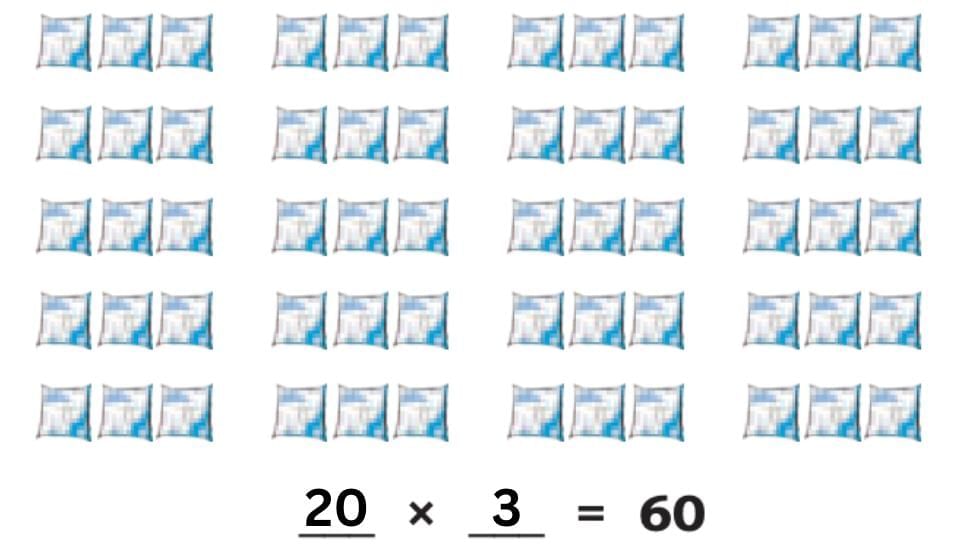 Here the pouches are arranged in 3 groups.
Here the pouches are arranged in 3 groups.
If you count, each group has 20 pouches.
So we write:
20 × 3 = 60
She made 10 groups of 6 → 10 × 6 = 60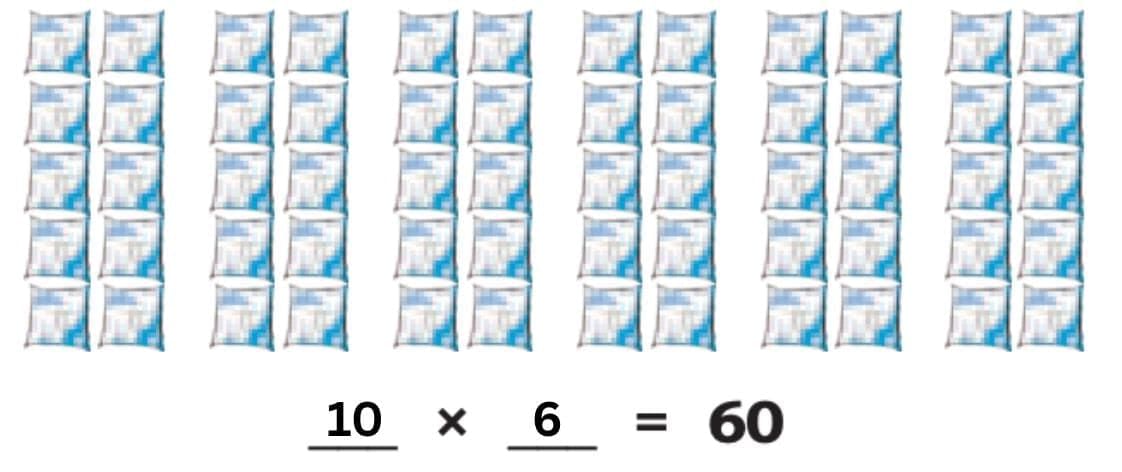 Here the pouches are arranged in 6 groups.
Here the pouches are arranged in 6 groups.
If you count, each group has 10 pouches.
So we write:
10 × 6 = 60
Conclusion
Total remains the same
No matter how the pouches are grouped (2, 3, 6, etc.), the total number of pouches is always 60.
Factors of 60
The numbers used in grouping (2, 3, 6, 10, 20, 30) are all factors of 60.
The relation between division and multiplication
60 ÷ 2 = 30
→ 30 × 2 = 60
60 ÷ 3 = 20
→ 20 × 3 = 60
60 ÷ 6 = 10
→ 10 × 6 = 60
General understanding
The same total can be arranged in different equal groups because a number can have many factors.
Let Us Think
The given shapes stand for numbers between 1 and 24. The same shape denotes the same number across all problems. Find the numbers hiding in all the shapes.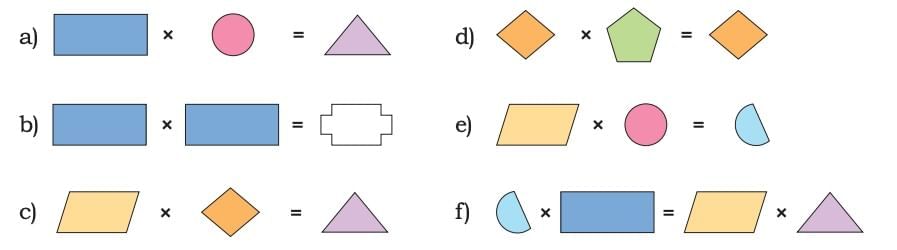
Sol:
We are told each shape stands for a number between 1 and 24. The same shape has the same number in all problems.
(a)  Rectangle × Circle = Triangle
Rectangle × Circle = Triangle
Rectangle = 3. So, 3 × Circle = Triangle.
If Circle = 4, then Triangle = 12.
Circle = 4, Triangle = 12
(b) 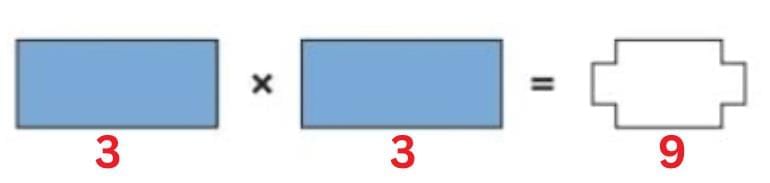 Rectangle × Rectangle = White shape
Rectangle × Rectangle = White shape
So, Rectangle × Rectangle = White shape.
If Rectangle = 3, then White shape = 3 × 3 = 9.
Rectangle = 3, White shape = 9
(c)  Parallelogram × Diamond = Triangle
Parallelogram × Diamond = Triangle
Diamond = 6, Triangle = 12.
So, Parallelogram × 6 = 12 → Parallelogram = 2.
Parallelogram = 2, Diamond = 6
(d) 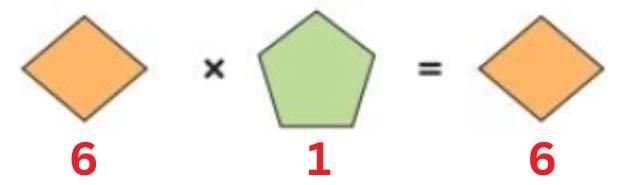 Diamond × Pentagon = Diamond
Diamond × Pentagon = Diamond
This means the number of the pentagon must be 1, because any number × 1 = the same number.
Pentagon = 1
(e) Parallelogram × Circle = Semicircle
Parallelogram × Circle = Semicircle
Parallelogram = 2, Circle = 4.
So, 2 × 4 = 8 → Semicircle = 8.
Semicircle = 8
(f)  Semicircle × Rectangle = Parallelogram × Triangle
Semicircle × Rectangle = Parallelogram × Triangle
8 × 3 = 24 and 2 × 12 = 24 → Both sides equal. Correct.
Order of Numbers in Multiplication
Daljeet arranged the butter packets in 7 rows with 6 packets in each row. That gave her
7 × 6 = 42 packets.
Now, what if she arranged them in 6 rows with 7 packets in each row?
This is written as 6 × 7. The total is still 42!
The number of packets does not change; only the way we arrange them changes.
This is called the Commutative Property of multiplication.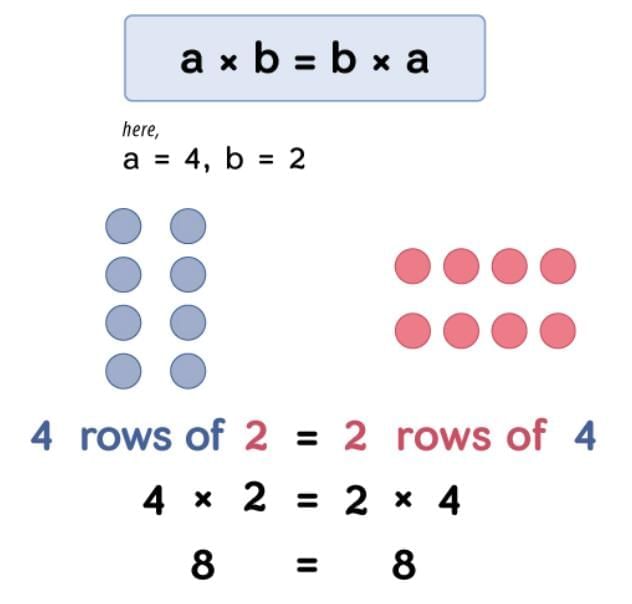
Let us discuss

Solution:
Number of groups = 6, Group size = 13
6 × 13 = 13 + 13 + 13 + 13 + 13 + 13 = 78
If we swap: 13 × 6 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 78
Both give 78.
This shows the Commutative Property of Multiplication
Let's Explore

Solution:
9 × 0
→ 9 groups of 0
→ 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 0
0 × 9
→ 0 groups of 9
→ Nothing to add → 0
This shows the Multiplication by Zero Property → a × 0 = 0 × a = 0
So, order doesn’t matter. But what happens when we make numbers ten times bigger?
Patterns in Multiplying by 10s and 100s
1. Multiplying by 10
- When we multiply a number by 10, it becomes 10 times bigger.
- Each digit moves one place to the left in the place value table.

- Quick Tip: Multiplying a number by 10 simply places one zero at the end.
2. Multiplying by 100
- When we multiply a number by 100, it becomes 100 times bigger.
- Each digit moves two places to the left in the place value table.
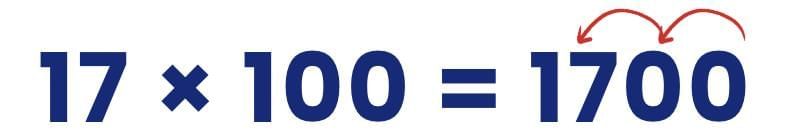
- Quick Tip: Multiplying a number by 100 simply places two zeros at the end.
Example: 30 × 20
Think of 30 as 3 × 10 and 20 as 2 × 10.
Now multiply step by step:
What will happen if we multiply numbers by 1,000?
- When we multiply a number by 1000, it becomes 1000 times bigger.
- Each digit moves three places to the left in the place value table.
- Example:
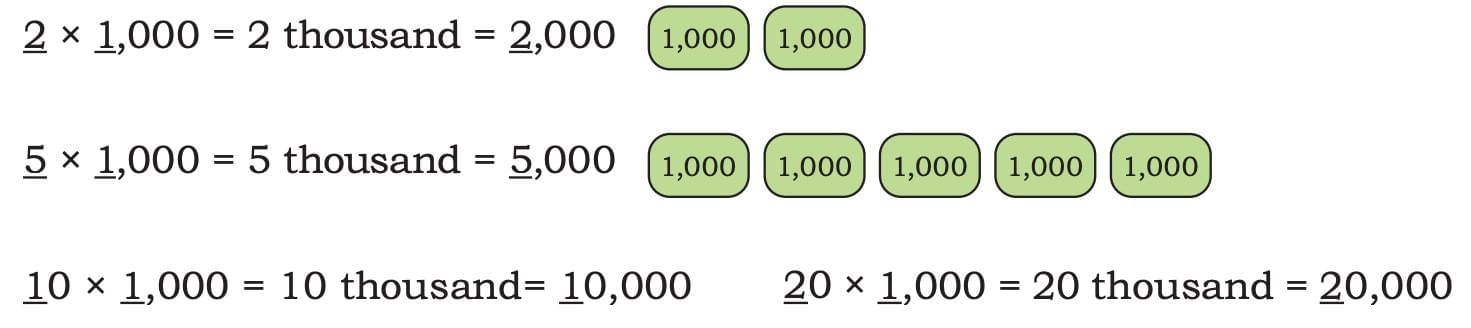
- Quick Tip: Multiplying a number by 1000 simply places three zeros at the end.
Multiplying by 10, 100, or 1000 is a quick shortcut—you simply add the same number of zeroes to the end of the number. But not all numbers are that neat. Let’s explore different strategies to handle such cases.
Many Ways to Multiply
- Multiplication can be solved in many ways.
- This shows multiplication is flexible, and we can choose the method that looks easiest to us.
- Take a look at the following example:

- 1. Breaking into Half and Double
- Half of 18 is 9.
- 9 × 5 = 45, and again 9 × 5 = 45.
- Add them: 45 + 45 = 90.
- 2. Doubling Strategy
- Double 18 to get 36.
- Double 36 to get 72.
- Add 18 more: 72 + 18 = 90.
- 3. Splitting Numbers (Distributive Property)
- Split 18 into 10 and 8.
- 10 × 5 = 50, 8 × 5 = 40.
- Add them: 50 + 40 = 90.
- 4. Using Equivalent Multiplication
- 18 × 5 = 9 × 10 (because 18 is 9 × 2, and 5 is 10 ÷ 2).
- 9 × 10 = 90.
- 5. Nearest Multiple Method
- 20 × 5 = 100.
- Subtract 2 × 5 = 10.
- 100 – 10 = 90.
Doubling and Halving
If we halve one number and double the other number, the answer remains the same.
Let’s understand this through an example:

- Start with 3 × 18.
- Double 3 → 6.
- Half of 18 → 9.
- Now, 6 × 9 = 54.
Both 3 × 18 and 6 × 9 give the same result: 54.
Why does it work?
Multiplication is like making groups.
If the groups are made half small but the number of groups doubles, the total stays the same.
That’s why 3 groups of 18 and 6 groups of 9 both give 54 objects.
Try It Yourself
Butter packets are arranged in the following ways. Let us find some strategies to calculate the total number of packets.
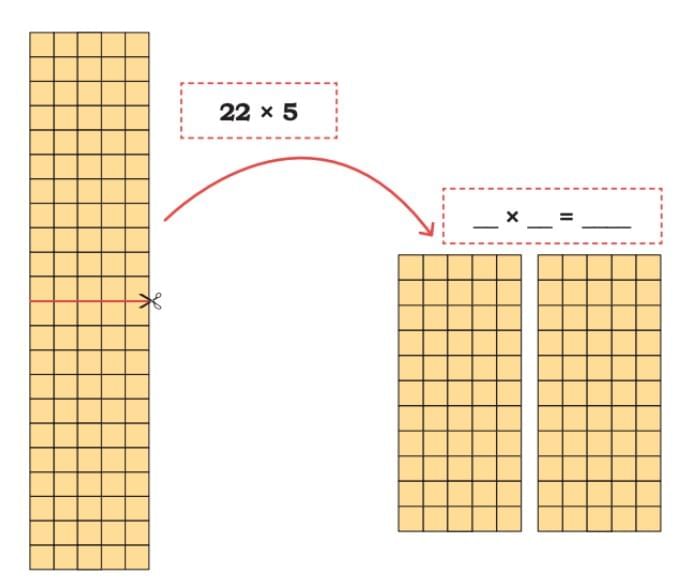
 View Answer
View Answer 
We need to find 22 × 5.
- I will half 22 and double 5.
- Half of 22 is 11.
- Double of 5 is 10.
- Now, 11 × 10 = 110.
So, 22 × 5 = 110.
Nearest Multiple
Sometimes, multiplication becomes easier if we round one number to the nearest multiple of 10 and then adjust the answer.
Let’s understand this through examples
(a) 4 × 19

1. Notice that 19 is close to 20.
2. Instead of multiplying directly with 19, take the nearest multiple of 10, i.e., 20.
3. But 19 is 1 less than 20, and since we are multiplying by 4, we must subtract 4 (i.e., 4 × 1).
Let's Explore

Because when we did 4 × 20, we counted one extra group of 4.
To correct it, we subtract that extra 4.
(b) 14 × 21
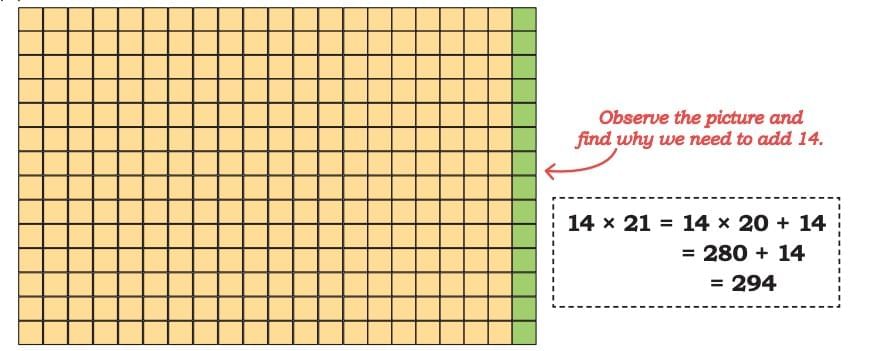
1. Notice that 21 is close to 20.
2. Instead of multiplying directly with 21, use the nearest multiple of 10, i.e., 20.
3. But 21 is 1 more than 20, so we must add one more group of 14.
Let's Explore

Because when we did 14 × 20, we counted one group of 14 less.
Since 21 = (20 + 1), we need to add back that missing 14.
Waste and Composting
Multiplication by Breaking Numbers into Parts
- Sometimes, it is difficult to multiply big numbers directly.
- We can make it easier by breaking numbers into smaller parts (expanded form).
- Expanded form means writing a number as the sum of tens and ones (or hundreds, tens, ones).
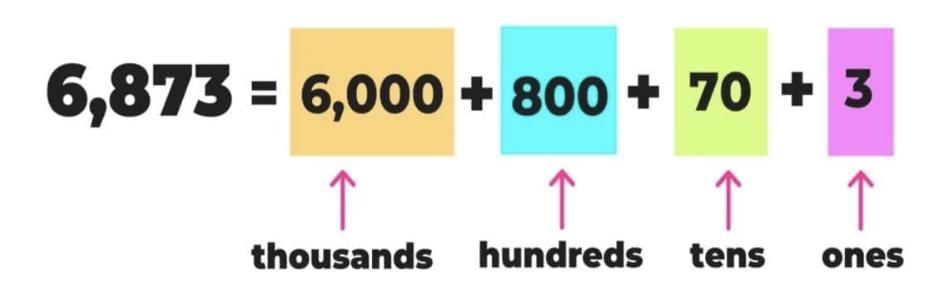
- After breaking, we multiply each part separately.
- Finally, we add all the partial products to get the total.
Let’s understand this through an example:
A family of 4 produces around 35 kg of kitchen waste in a month. How much waste will the family produce in a year?
Quantity of kitchen waste in 1 month is 35 kg.
Quantity of kitchen waste in 12 months is 12 × 35 kg.

Nida, Kanti, and John used different methods to solve the problem. Let’s go through them one by one.
(a) Nida's Way 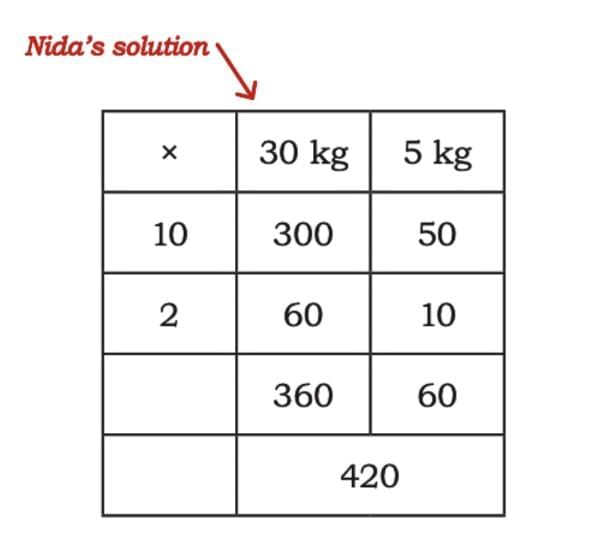
Instead of doing it directly, Nida has broken the numbers into parts to make multiplication easier.
Step 1: Break the Numbers
Split 35 into 30 + 5
Split 12 into 10 + 2
Step 2: Multiply in Parts
10 × 30 = 300
10 × 5 = 50
2 × 30 = 60
2 × 5 = 10
Step 3: Add Them Together
(b) Kanti's Way
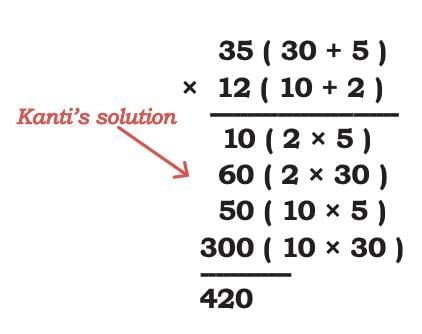
Let’s go through this step by step.
Step 1: Take the 2 from (10 + 2) and multiply with the 5 from (30 + 5):
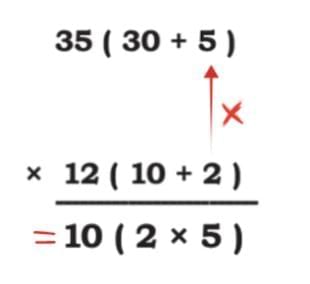
Step 2: Next, take the 2 and multiply with the 30:
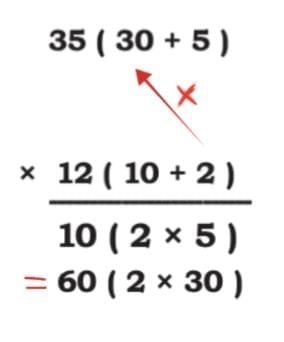
Step 3: Now, take the 10 (from 10 + 2) and multiply with the 5:

Step 4: Finally, take the 10 and multiply with the 30:
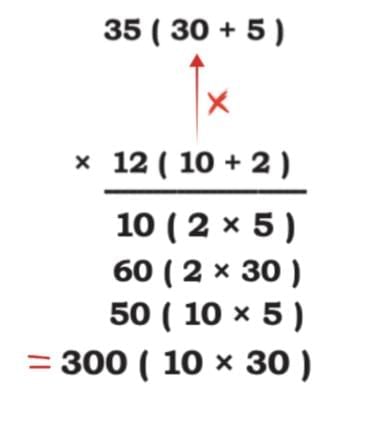
Step 5: Now we add all the partial results:
10 + 60 + 50 + 300 = 420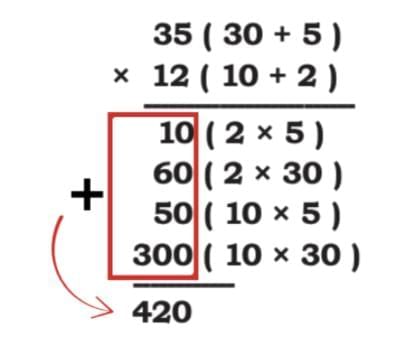
So, 35 × 12 = 420
(a) John's Way

35 = (30 + 5)
12 = (10 + 2)
Step 1: Multiply 2 with each part of 35
Together → 60 + 10 = 70 (which is 2 × 35)
Step 2: Multiply 10 with each part of 35Together → 300 + 50 = 350 (which is 10 × 35)
Step 3: Add the two results
70 + 350 = 420
So, 35 × 12 = 420
Dairy Cooperative
Multiplying a 3-Digit Number by a 1-Digit Number
There are two simple methods to do this.
Let’s understand both methods with the help of the following example:
A dairy cooperative in a small town gets its milk from 268 villagers. Each villager has at least 4 milk-giving cows.

1. What is the minimum number of cows the dairy cooperative gets its milk from?1 villager has at least 4 milk-giving cows. 268 villagers will have at least 268 × 4 cows.
Method 1: Expanded Form Method

Break the number
268 = 200 + 60 + 8
Now multiply each part by 4:
- 200 × 4 = 800
- 60 × 4 = 240
- 8 × 4 = 32
Now add them:
800 + 240 + 32 = 1,072
Method 2: Short Method (Column Multiplication)
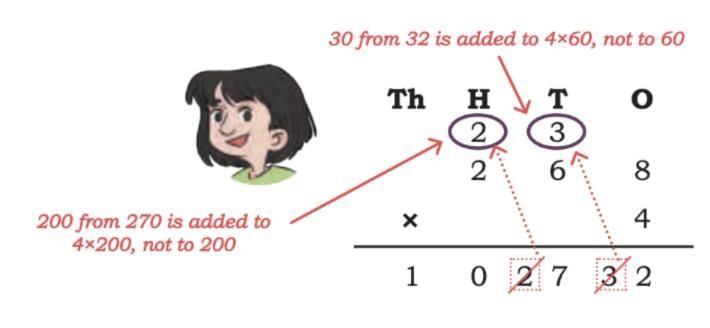
- Multiply ones: 8 × 4 = 32 → write 2, carry 3.
- Multiply tens: 6 × 4 = 24, plus the carry 3 = 27 → write 7, carry 2.
- Multiply hundreds: 2 × 4 = 8, plus the carry 2 = 10 → write 10.
So, the answer is 1,072
Important to Remember
Carry is not just a single digit; it has a value.
- 3 carried from 32 means 30 (3 tens).
- 2 carried from 270 means 200 (2 hundreds).
- That is why we add the carry to the next place value, not to the small number.
Check! Check!
Check if the following children’s solutions are correct. If correct, explain why the solution is correct. If it is incorrect, then identify the error and correct the solution.
Give it a try first, then match with the solution.
The King's Reward
Repeated Multiplication
- Repeated multiplication means multiplying the same number again and again.
- It is a faster way of growing numbers compared to addition.
- Example: 2 × 2 × 2 × 2 = 16.
- Repeated multiplication is written using powers (like 2⁴ = 16).
- This idea helps us understand how numbers become very large quickly.
One day, a king decided to reward three of his most talented ministers. The king called them to his court and said, “You all have served my empire with great dedication. As a reward, I give you three choices of gold.
Choose wisely!
Choice 1: Take 5 gold coins and double the number of coins every day for 7 days.
Choice 2: Take 3 gold coins and triple the number of coins every day for 7days.
Choice 3: Take 1 gold coin and multiply the number of coins by 5 every day for 7 days.
Minister 1—I will take 5 gold coins and double the number of coins every day for 7 days.
Minister 2—I will take 3 gold coins and triple the number of coins every day for 7 days.
Minister 3—I will take 1 gold coin and multiply the number of coins by 5every day for 7 days.
The King gave 5 coins to Minister 1, 3 coins to Minister 2 and 1 coin to Minister 3. Which of the rewards would you have chosen? After a week, the 3 ministers were surprised at the final amount of gold coins. Guess who received the most gold coins? Calculate how many gold coins each minister received.
Sol: The king gave 3 choices. Every day, the coins are multiplied.
Minister 1 — start 5 coins, double (×2) for 7 days
Day 0: 5
Day 1: 5 × 2 = 10
Day 2: 10 × 2 = 20
Day 3: 20 × 2 = 40
Day 4: 40 × 2 = 80
Day 5: 80 × 2 = 160
Day 6: 160 × 2 = 320
Day 7: 320 × 2 = 640
So total after 7 days = 640
(Quick check: 5 × 2⁷ = 5 × 128 = 640)
Minister 2 — start 3 coins, triple (×3) for 7 days
Day 0: 3
Day 1: 3 × 3 = 9
Day 2: 9 × 3 = 27
Day 3: 27 × 3 = 81
Day 4: 81 × 3 = 243
Day 5: 243 × 3 = 729
Day 6: 729 × 3 = 2,187
Day 7: 2,187 × 3 = 6,561
So total after 7 days = 6,561
(Quick check: 3 × 3⁷ = 3⁸ = 6,561)
Minister 3 — start 1 coin, multiply by 5 (×5) for 7 days
Day 0: 1
Day 1: 1 × 5 = 5
Day 2: 5 × 5 = 25
Day 3: 25 × 5 = 125
Day 4: 125 × 5 = 625
Day 5: 625 × 5 = 3,125
Day 6: 3,125 × 5 = 15,625
Day 7: 15,625 × 5 = 78,125
So total after 7 days = 78,125
(Quick check: 1 × 5⁷ = 78,125)
Which reward to choose
Minister 1 doubled his coins and got 640.
Minister 2 tripled his coins and got 6,561.
Minister 3 multiplied by 5 and got 78,125.
Even though Minister 3 started with only 1 coin, he multiplied by a bigger number (×5). Multiplying by 5 again and again made the coins grow very fast. That is why Choice 3 gave the largest number of coins.
So the best choice is Choice 3, because multiplying by a bigger number every day gives the highest reward.
Final answers
Minister 1: 640 coins
Minister 2: 6,561 coins
Minister 3: 78,125 coins
Most coins: Minister 3.
Multiplication Patterns
- In multiplication, the numbers we multiply are called multiplicand and multiplier.
- The answer we get is called the product.
- Sometimes, when we change the multiplier or multiplicand, the product also changes in a pattern.
Observe and complete the given patterns
a) 1 × 1 = 1
1 × 1 = 1
11 × 11 = 121
111 × 111 = 12,321
1111 × 1111 = 1,234,321
Explanation: when a number has only 1s and we square it, the digits go up 1–2–3–4 and then come back down 3–2–1.
b)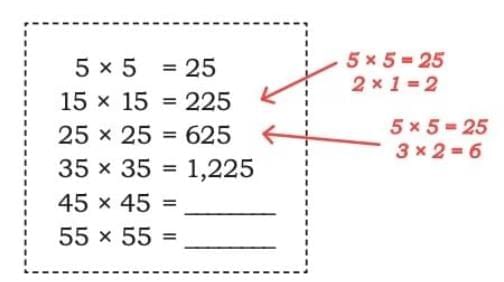 5 × 5 = 25
5 × 5 = 25
15 × 15 = 225
25 × 25 = 625
35 × 35 = 1,225
45 × 45 = 2,025
55 × 55 = 3,025
Explanation: any number ending with 5, say a5, squared is a × (a + 1) followed by 25.
Example: 45² → 4 × 5 = 20, then write 25 → 2,025.
c) 11 × 12 = 132
11 × 12 = 132
11 × 34 = 374
11 × 56 = 616
11 × 78 = 858
11 × 54 = 594
11 × 82 = 902
Explanation: 11 × ab (two-digit ab) becomes a (a+b) b. If a+b is 10 or more, put the 0 in the middle and carry 1 to the first digit.
For 82: 8 (8+2=10) 2 → carry 1 to 8 → 902.
d)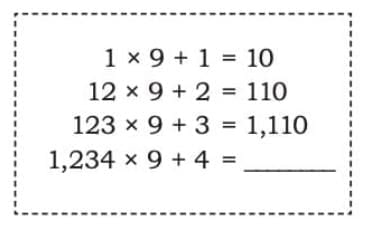 1 × 9 + 1 = 10
1 × 9 + 1 = 10
12 × 9 + 2 = 110
123 × 9 + 3 = 1,110
1,234 × 9 + 4 = 11,110
Explanation: multiply the counting numbers 1, 12, 123, 1234 by 9 and add the last digit. The answer becomes all 1s with a zero at the end.
Remember number pairs from Grade 4? Any two adjacent numbers in a row or a column are number pairs. Can you identify the pair whose product is the smallest and another pair whose product is the largest? Do you need to find every product or can you find this by looking at the numbers?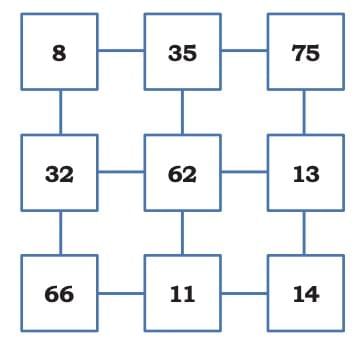
Sol:
Horizontal products: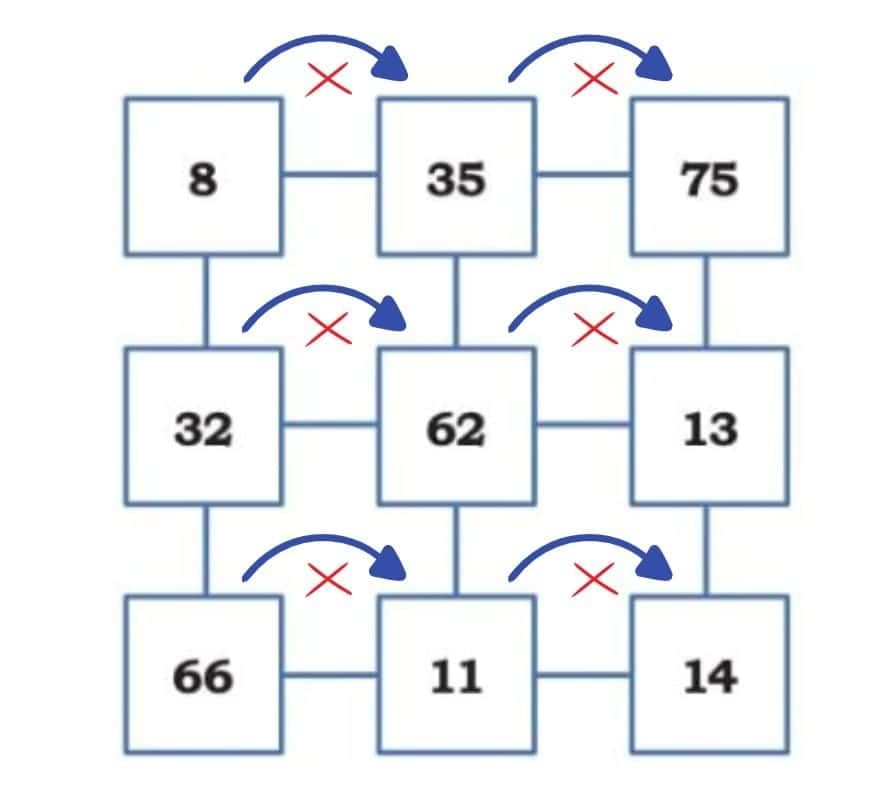 Row 1
Row 1
Row 2:
Row 3
Vertical products: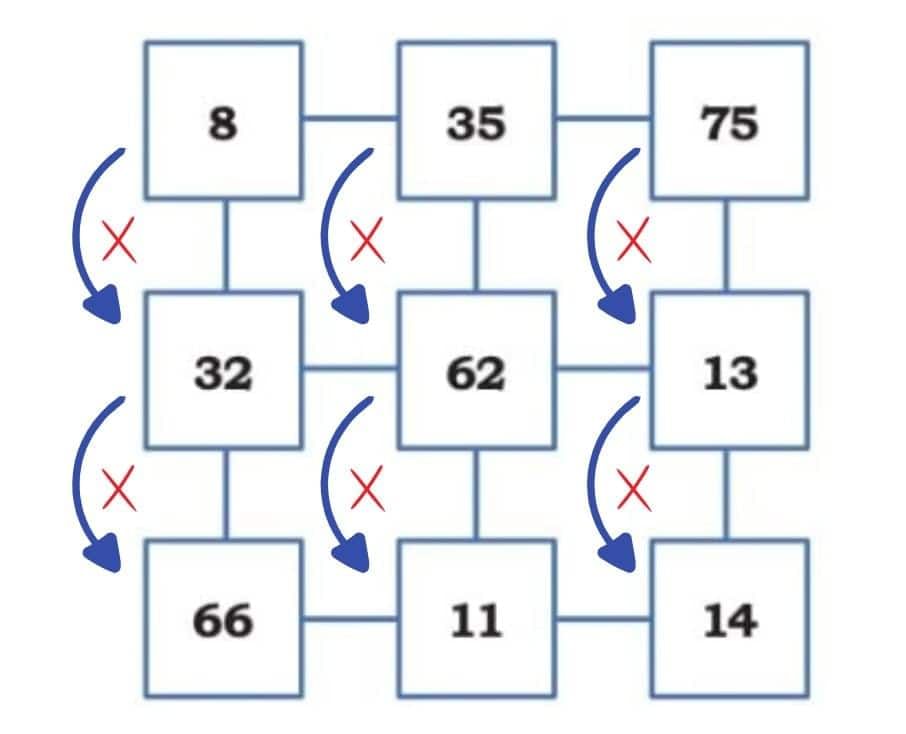 Column 1
Column 1
Column 2
- 35×62 = 2,170
- 62×11 = 682
Column 3
Smallest product = 11 and 14 → 154
Largest product = 35 and 75 → 2,625
To find the smallest and largest products, look for the smallest adjacent pair and the largest adjacent pair. You don’t need to multiply all pairs.
Find by looking:
- Smallest adjacent pair: 11 and 14 → product will be smallest.
- Largest adjacent pair: 35 and 75 → product will be largest.
When numbers are multiplied, bigger numbers give bigger products and smaller numbers give smaller products. So instead of multiplying everything, we can look for the smallest adjacent pair and the largest adjacent pair.


 Can you imagine doing this one by one? That’s why multiplication is so helpful!
Can you imagine doing this one by one? That’s why multiplication is so helpful!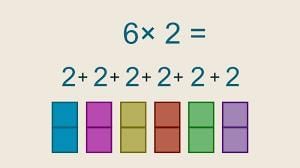
 Here we see that multiplication is a faster and easier way to find the total than adding again and again.
Here we see that multiplication is a faster and easier way to find the total than adding again and again.



 Rectangle × Circle = Triangle
Rectangle × Circle = Triangle Rectangle × Rectangle = White shape
Rectangle × Rectangle = White shape Parallelogram × Diamond = Triangle
Parallelogram × Diamond = Triangle Diamond × Pentagon = Diamond
Diamond × Pentagon = Diamond Parallelogram × Circle = Semicircle
Parallelogram × Circle = Semicircle Semicircle × Rectangle = Parallelogram × Triangle
Semicircle × Rectangle = Parallelogram × Triangle



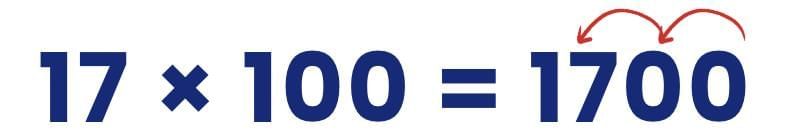














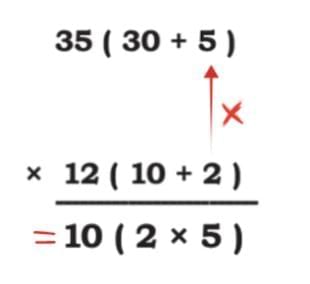
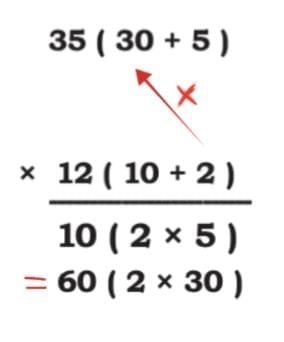

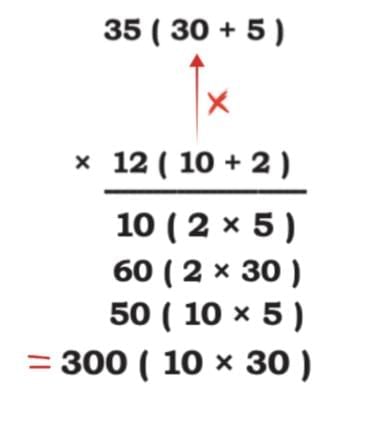






 Asma’s solution (46 × 59)
Asma’s solution (46 × 59)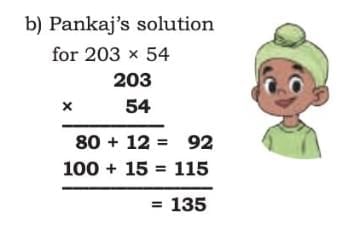 Pankaj’s solution (203 × 54)
Pankaj’s solution (203 × 54)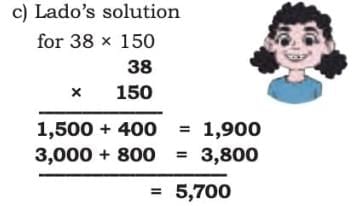 Lado’s solution (38 × 150)
Lado’s solution (38 × 150)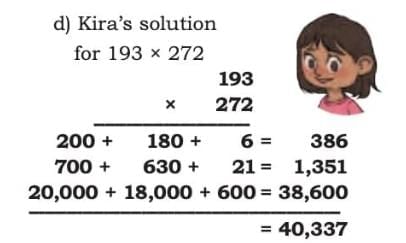 Kira’s solution (193 × 272)
Kira’s solution (193 × 272)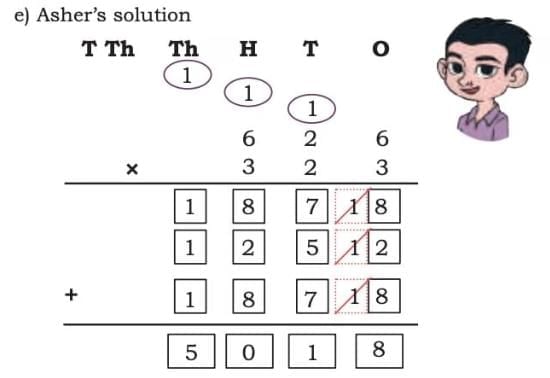 Asher’s solution (626 × 323)
Asher’s solution (626 × 323) 1 × 1 = 1
1 × 1 = 1 5 × 5 = 25
5 × 5 = 25 11 × 12 = 132
11 × 12 = 132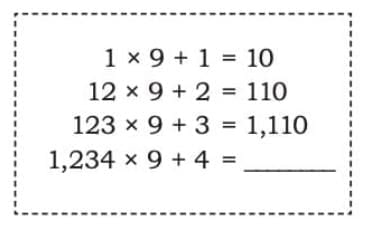 1 × 9 + 1 = 10
1 × 9 + 1 = 10
 Row 1
Row 1 Column 1
Column 1














