Practice Question - 11 (Venn Diagram) | 100 DILR Questions for CAT Preparation PDF Download
A speciality supermarket sells 320 products. Each of these products was either a cosmetic product or a nutrition product. Each of these products was also either a foreign product or a domestic product. Each of these products had at least one of the two approvals - FDA or EU.
The following facts are also known:
1. There were equal numbers of domestic and foreign products.
2. Half of the domestic products were FDA approved cosmetic products.
3. None of the foreign products had both the approvals, while 60 domestic products had both the approvals.
4. There were 140 nutrition products, half of them were foreign products.
5. There were 200 FDA approved products. 70 of them were foreign products and 120 of them were cosmetic products.
Q1: How many foreign products were FDA approved cosmetic products?
View Answer 
Ans: 40
It is given that the total number of products supermarket sells is 320.
cosmetic + nutrition = foreign + domestic = FDA + EU = 320 products
In statement 1, it is given that the number of foreign products is equal to the number of domestic products.
Foreign products = Domestic products = 320/2 = 160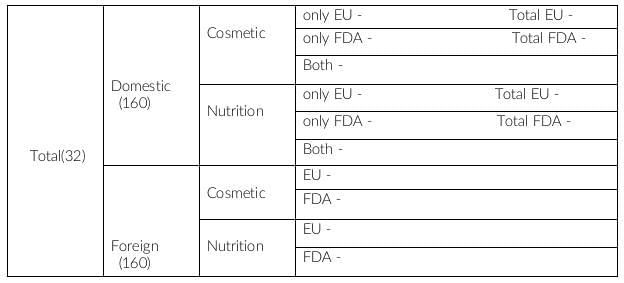
In statement 2, it is given that half of the domestic products were FDA approved cosmetic products, i.e. domestic, cosmetic and FDA = 80
In statement 4, it is given that there were 140 nutrition products, half of them were foreign products. This implies remaining half are domestic.
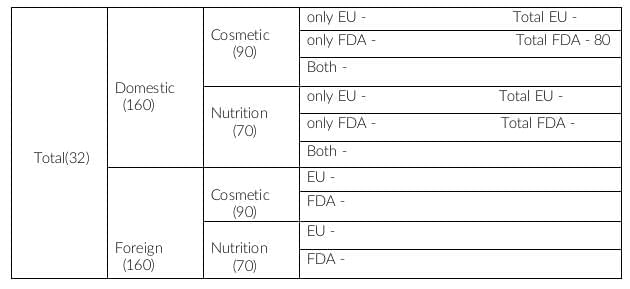
In statement 5, it is given that there are 200 FDA approved products out of which 70 are foreign products and 120 are cosmetic products.
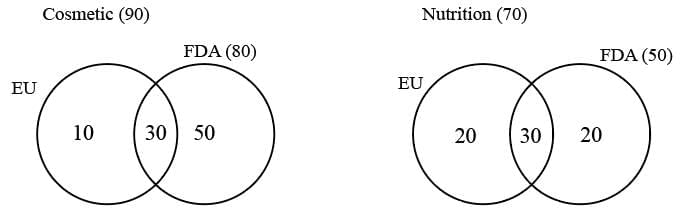
If 70 are foreign products, remaining 130 should be domestic products. In domestic products, FDA approved cosmetic products are 80. This implies FDA approved nutrition products are 130-80, i.e. 50.
There are 120 FDA approved cosmetic products.
Domestic, cosmetic and FDA approved = 80
This implies, Foreign, cosmetic and FDA approved is 120-80, i.e. 40.
There are 70 FDA approved foreign products.
This implies Foreign, nutrition and FDA approved is 70-40, i.e. 30.
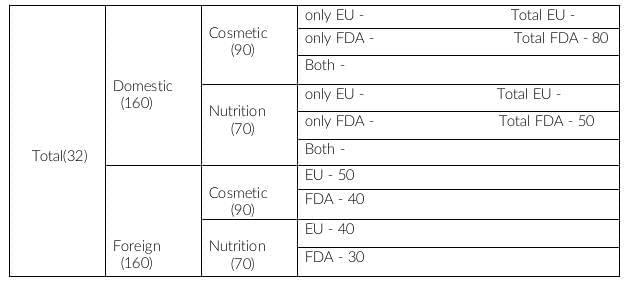
Domestic and Cosmetic = 90
Domestic, comestic and FDA approved = 80
This implies, Domestic, cosmetic and FDA not approved is 90-80, i.e. 10.
Therefore, (domestic, cosmetic and only EU) = 10
Similarly, we get (domestic, nutrition and only EU) = 70-50 = 20
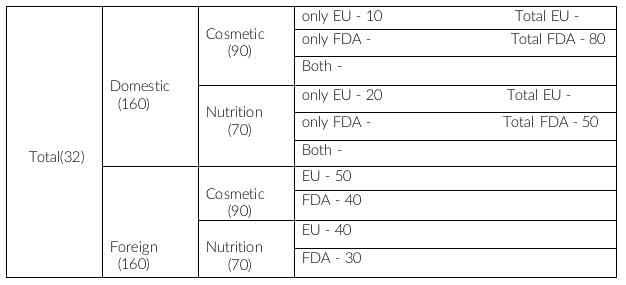
The number of foreign, cosmetic and FDA approved products is 40.
The answer is 40.
Q2: How many cosmetic products did not have FDA approval?
(a) 10
(b) Cannot be determined
(c) 50
(d) 60
View Answer Ans: (d)
It is given that the total number of products supermarket sells is 320.
cosmetic + nutrition = foreign + domestic = FDA + EU = 320 products
In statement 1, it is given that the number of foreign products is equal to the number of domestic products.
Foreign products = Domestic products = 320/2 = 160
In statement 2, it is given that half of the domestic products were FDA approved cosmetic products, i.e. domestic, cosmetic and FDA = 80
In statement 4, it is given that there were 140 nutrition products, half of them were foreign products. This implies remaining half are domestic.
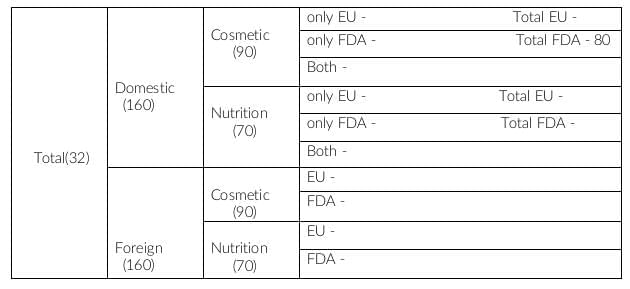
In statement 5, it is given that there are 200 FDA approved products out of which 70 are foreign products and 120 are cosmetic products.
If 70 are foreign products, remaining 130 should be domestic products. In domestic products, FDA approved cosmetic products are 80. This implies FDA approved nutrition products are 130-80, i.e. 50.
There are 120 FDA approved cosmetic products.
Domestic, cosmetic and FDA approved = 80
This implies, Foreign, cosmetic and FDA approved is 120-80, i.e. 40.
There are 70 FDA approved foreign products.
This implies Foreign, nutrition and FDA approved is 70-40, i.e. 30.
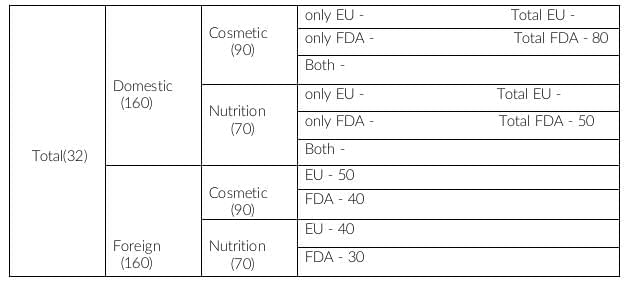
Domestic and Cosmetic = 90
Domestic, comestic and FDA approved = 80
This implies, Domestic, cosmetic and FDA not approved is 90-80, i.e. 10.
Therefore, (domestic, cosmetic and only EU) = 10
Similarly, we get (domestic, nutrition and only EU) = 70-50 = 20
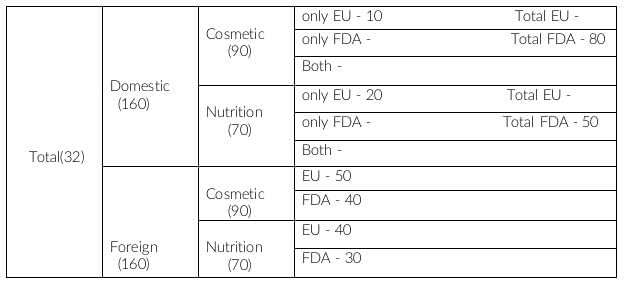
The number of cosmetic products which do not have FDA approval = domestic only EU + foreign EU = 10 + 50 = 60
The answer is option (d).
Q3: Which among the following options best represents the number of domestic cosmetic products that had both the approvals?
(a) At least 10 and at most 60
(b) At least 10 and at most 80
(c) At least 20 and at most 70
(d) At least 20 and at most 50
View Answer Ans: (a)
It is given that the total number of products supermarket sells is 320.
cosmetic + nutrition = foreign + domestic = FDA + EU = 320 products
In statement 1, it is given that the number of foreign products is equal to the number of domestic products.
Foreign products = Domestic products = 320/2 = 160
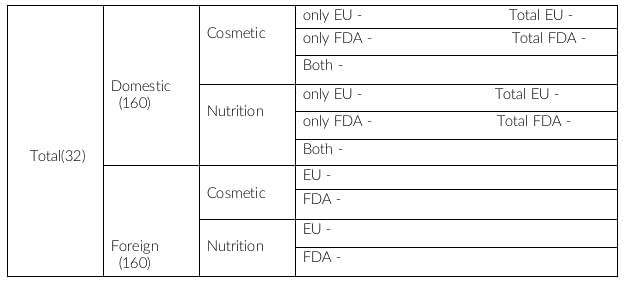
In statement 2, it is given that half of the domestic products were FDA approved cosmetic products, i.e. domestic, cosmetic and FDA = 80
In statement 4, it is given that there were 140 nutrition products, half of them were foreign products. This implies remaining half are domestic.
In statement 5, it is given that there are 200 FDA approved products out of which 70 are foreign products and 120 are cosmetic products.
If 70 are foreign products, remaining 130 should be domestic products. In domestic products, FDA approved cosmetic products are 80. This implies FDA approved nutrition products are 130-80, i.e. 50.
There are 120 FDA approved cosmetic products.
Domestic, cosmetic and FDA approved = 80
This implies, Foreign, cosmetic and FDA approved is 120-80, i.e. 40.
There are 70 FDA approved foreign products.
This implies Foreign, nutrition and FDA approved is 70-40, i.e. 30.
Domestic and Cosmetic = 90
Domestic, comestic and FDA approved = 80
This implies, Domestic, cosmetic and FDA not approved is 90-80, i.e. 10.
Therefore, (domestic, cosmetic and only EU) = 10
Similarly, we get (domestic, nutrition and only EU) = 70-50 = 20
In statement 3, it is given that the number of domestic products which have both the approvals = 60
In the question, it is given that a + c = 60
To find the minimum value of a, we need to maximise c.
Maximum value c can take is 50
Therefore, minimum value of a is 60-50, i.e. 10.
To find the maximum value of a, we need to minimise c.
Maximum value c can take is 0.
Therefore, maximum value of a is 60-0, i.e. 60.
a is minimum:
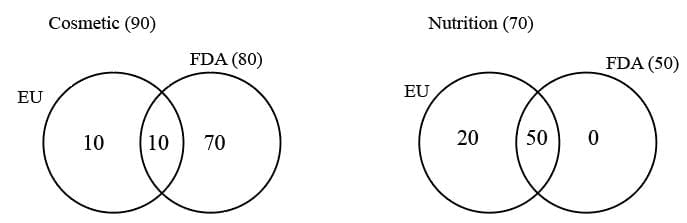
a is maximum:
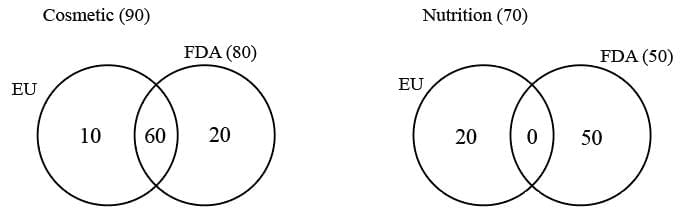
Therefore, the number of domestic cosmetic products that had both the approvals is at least 10 and at most 60.
The answer is option (a).
Q4: If 70 cosmetic products did not have EU approval, then how many nutrition products had both the approvals?
(a) 50
(b) 30
(c) 10
(d) 20
View Answer Ans: (c)
It is given that the total number of products supermarket sells is 320.
cosmetic + nutrition = foreign + domestic = FDA + EU = 320 products
In statement 1, it is given that the number of foreign products is equal to the number of domestic products.
Foreign products = Domestic products = 320/2 = 160
In statement 2, it is given that half of the domestic products were FDA approved cosmetic products, i.e. domestic, cosmetic and FDA = 80
In statement 4, it is given that there were 140 nutrition products, half of them were foreign products. This implies remaining half are domestic.
In statement 5, it is given that there are 200 FDA approved products out of which 70 are foreign products and 120 are cosmetic products.
If 70 are foreign products, remaining 130 should be domestic products. In domestic products, FDA approved cosmetic products are 80. This implies FDA approved nutrition products are 130-80, i.e. 50.
There are 120 FDA approved cosmetic products.
Domestic, cosmetic and FDA approved = 80
This implies, Foreign, cosmetic and FDA approved is 120-80, i.e. 40.
There are 70 FDA approved foreign products.
This implies Foreign, nutrition and FDA approved is 70-40, i.e. 30.
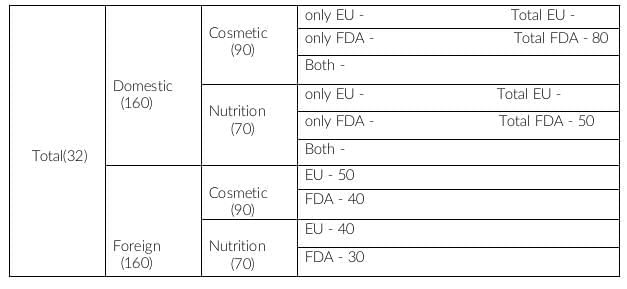
Domestic and Cosmetic = 90
Domestic, comestic and FDA approved = 80
This implies, Domestic, cosmetic and FDA not approved is 90-80, i.e. 10.
Therefore, (domestic, cosmetic and only EU) = 10
Similarly, we get (domestic, nutrition and only EU) = 70-50 = 20
In the question, it is given that 70 cosmetic products did not have EU approval.
In foreign, 40 cosmetic products did not have EU approval. This implies 30 cosmetic products should have only FDA approval in domestic products.
According to the above statement, b = 30
a = 80 - 30 = 50
Given, a + c = 60
c = 60 - 50 = 10
Therefore, the number of nutrition products which had both the approvals is 10.
The answer is option (c).
Q5: If 50 nutrition products did not have EU approval, then how many domestic cosmetic products did not have EU approval?
View Answer Ans: 50
It is given that the total number of products supermarket sells is 320.
cosmetic + nutrition = foreign + domestic = FDA + EU = 320 products
In statement 1, it is given that the number of foreign products is equal to the number of domestic products.
Foreign products = Domestic products = 320/2 = 160
In statement 2, it is given that half of the domestic products were FDA approved cosmetic products, i.e. domestic, cosmetic and FDA = 80
In statement 4, it is given that there were 140 nutrition products, half of them were foreign products. This implies remaining half are domestic.
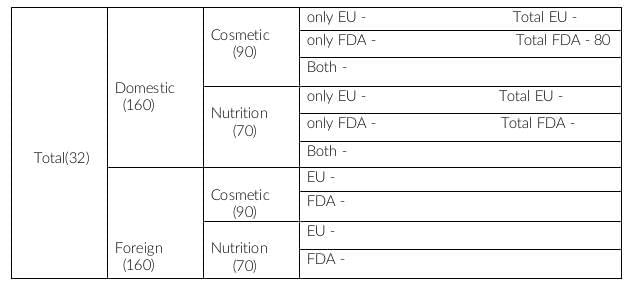
In statement 5, it is given that there are 200 FDA approved products out of which 70 are foreign products and 120 are cosmetic products.
If 70 are foreign products, remaining 130 should be domestic products. In domestic products, FDA approved cosmetic products are 80. This implies FDA approved nutrition products are 130-80, i.e. 50.
There are 120 FDA approved cosmetic products.
Domestic, cosmetic and FDA approved = 80
This implies, Foreign, cosmetic and FDA approved is 120-80, i.e. 40.
There are 70 FDA approved foreign products.
This implies Foreign, nutrition and FDA approved is 70-40, i.e. 30.
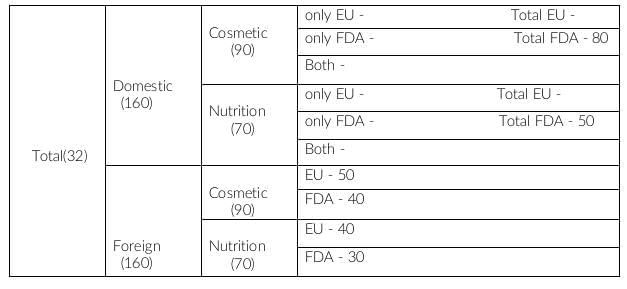
Domestic and Cosmetic = 90
Domestic, comestic and FDA approved = 80
This implies, Domestic, cosmetic and FDA not approved is 90-80, i.e. 10.
Therefore, (domestic, cosmetic and only EU) = 10
Similarly, we get (domestic, nutrition and only EU) = 70-50 = 20
In the question, it is given that 50 nutrition products did not have EU approval.
In Foreign products, there are 30 nutrition products which do not have EU approval. This implies 20 nutrition products do not have EU(have only FDA) approval in domestic products.
It is given, d = 20
c = 50 - 20 = 30
It is given, a + c = 60
a = 60 - 30 = 30
b = 80 - 30 = 50
Therefore, the number of domestic cosmetic products did not have EU(only FDA) approval is 50.
|
102 videos|123 docs|121 tests
|
FAQs on Practice Question - 11 (Venn Diagram) - 100 DILR Questions for CAT Preparation
| 1. What is a Venn diagram, and how is it used in problem-solving? |  |
| 2. How do you interpret the results of a Venn diagram in the context of a question? | |
| 3. What types of questions can be effectively solved using Venn diagrams? | |
| 4. Are there any specific strategies for solving Venn diagram problems in exams? | |
| 5. Can Venn diagrams be used for more than two sets, and how does that work? | |
Free
,Important questions
,study material
,practice quizzes
,Extra Questions
,Objective type Questions
,Summary
,MCQs
,Practice Question - 11 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,mock tests for examination
,past year papers
,Exam
,Previous Year Questions with Solutions
,Practice Question - 11 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,Viva Questions
,Practice Question - 11 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,ppt
,Semester Notes
,video lectures
,Sample Paper
,shortcuts and tricks
;
Practice Question - 11 (Venn Diagram) Free PDF Download
Importance of Practice Question - 11 (Venn Diagram)
Practice Question - 11 (Venn Diagram) Notes
Practice Question - 11 (Venn Diagram) CAT Questions
Study Practice Question - 11 (Venn Diagram) on the App
|
© EduRev
|
Education Revolution
|
|
