Practice Question - 12 (Venn Diagram) | 100 DILR Questions for CAT Preparation PDF Download
There are 15 girls and some boys among the graduating students in a class. They are planning a get-together, which can be either a 1-day event, or a 2-day event, or a 3-day event. There are 6 singers in the class, 4 of them are boys. There are 10 dancers in the class, 4 of them are girls. No dancer in the class is a singer.
Some students are not interested in attending the get-together. Those students who are interested in attending a 3-day event are also interested in attending a 2-day event; those who are interested in attending a 2-day event are also interested in attending a 1-day event.
The following facts are also known:
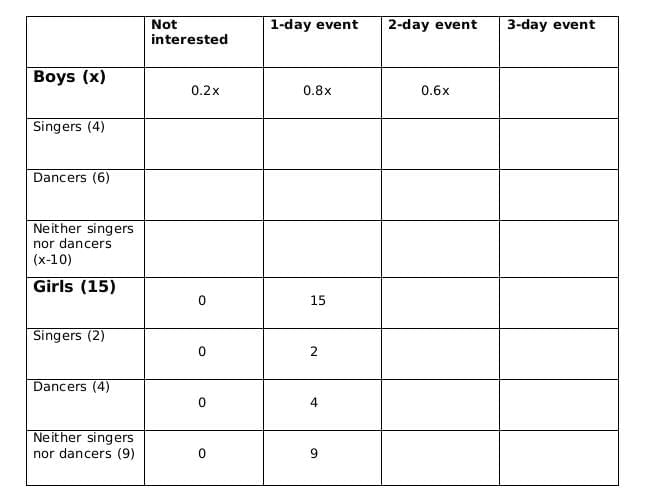
1. All the girls and 80% of the boys are interested in attending a 1-day event. 60% of the boys are interested in attending a 2-day event.
2. Some of the girls are interested in attending a 1-day event, but not a 2-day event; some of the other girls are interested in attending both.
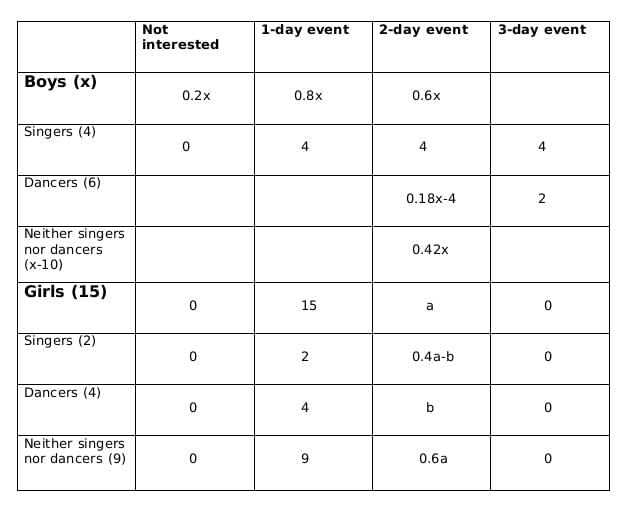
3. 70% of the boys who are interested in attending a 2-day event are neither singers nor dancers. 60% of the girls who are interested in attending a 2-day event are neither singers nor dancers.
4. No girl is interested in attending a 3-day event. All male singers and 2 of the dancers are interested in attending a 3-day event.
5. The number of singers interested in attending a 2-day event is one more than the number of dancers interested in attending a 2-day event.
Q1: How many boys are there in the class?
View Answer 
Ans: 50
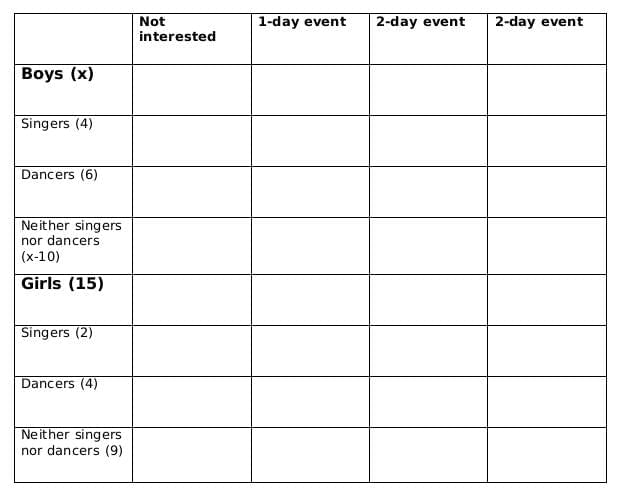
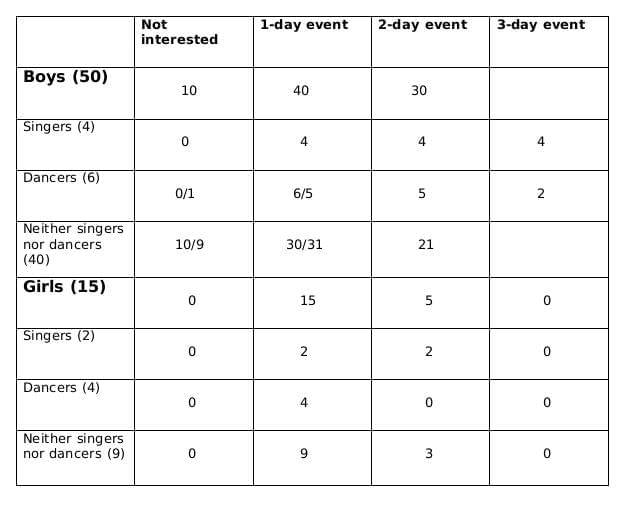
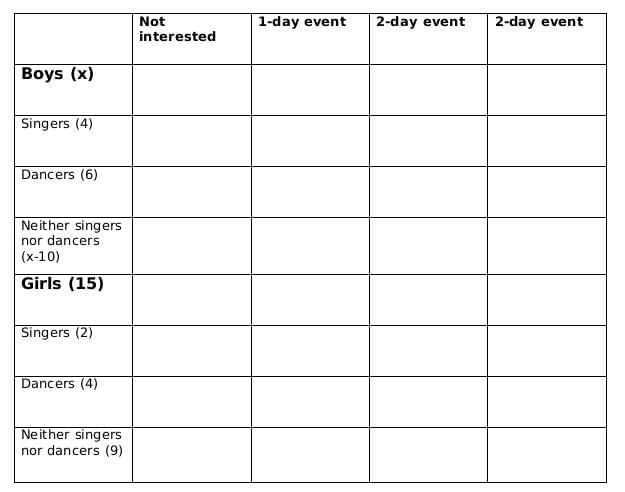
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
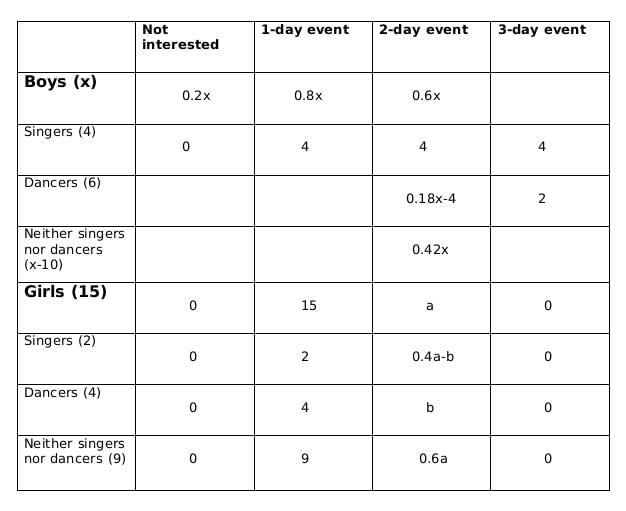
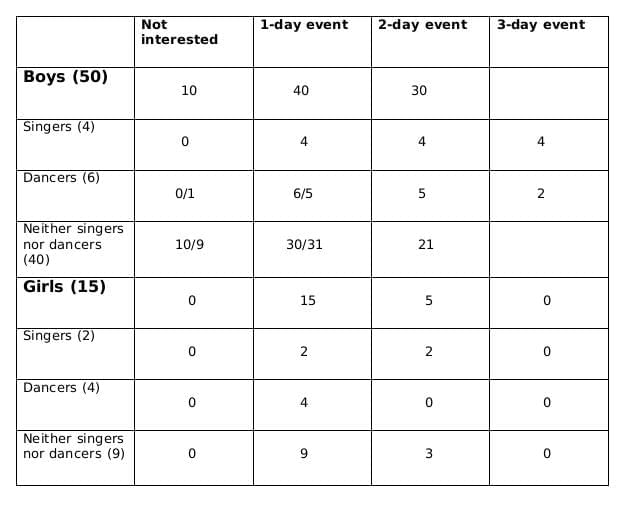
Now we fill the above table, using statements 1 and 2, we get the following table
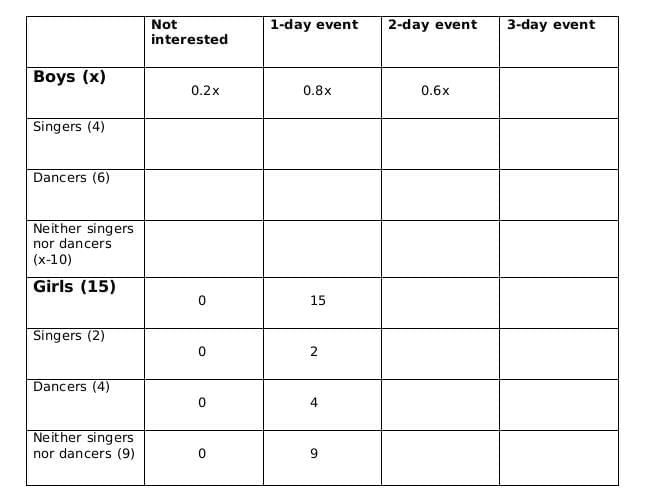
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
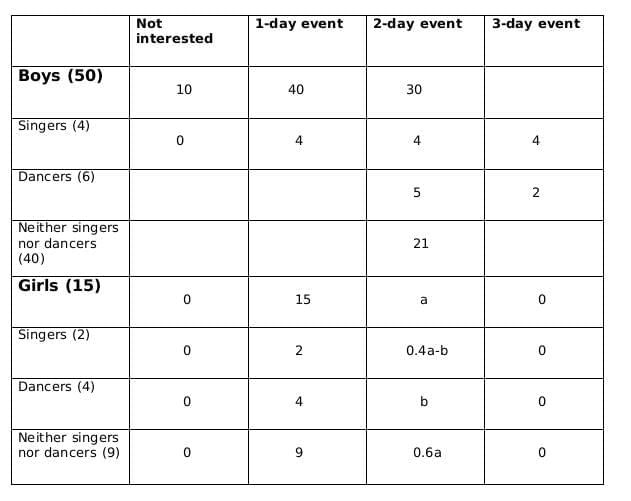
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
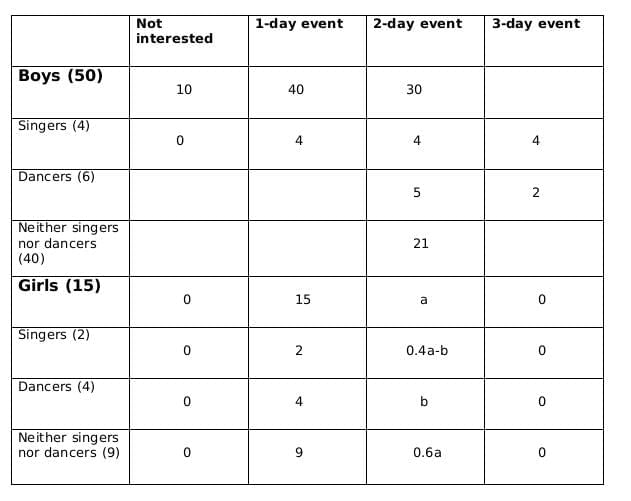
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
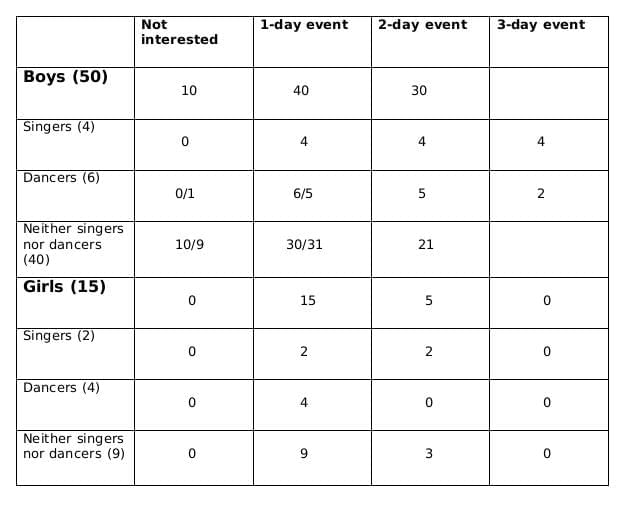
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
Q2: Which of the following can be determined from the given information?
I. The number of boys who are interested in attending a 1-day event and are neither dancers nor singers.
II. The number of female dancers who are interested in attending a 1-day event.
(a) Only I
(b) Neither I nor II
(c) Only II
(d) Both I and II
View Answer Ans: (c)
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
Now we fill the above table, using statements 1 and 2, we get the following table
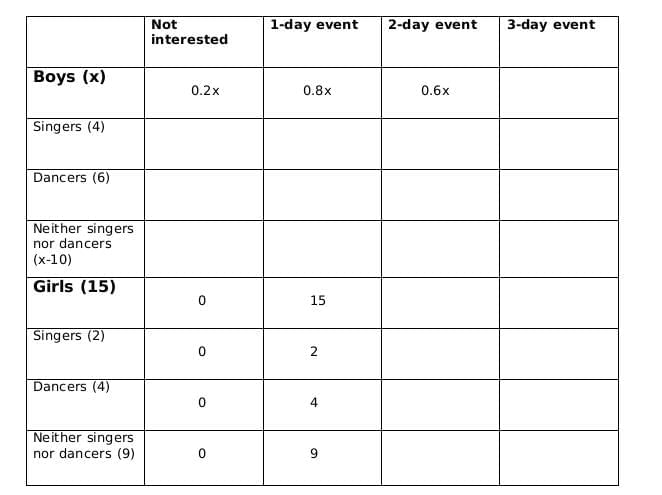
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
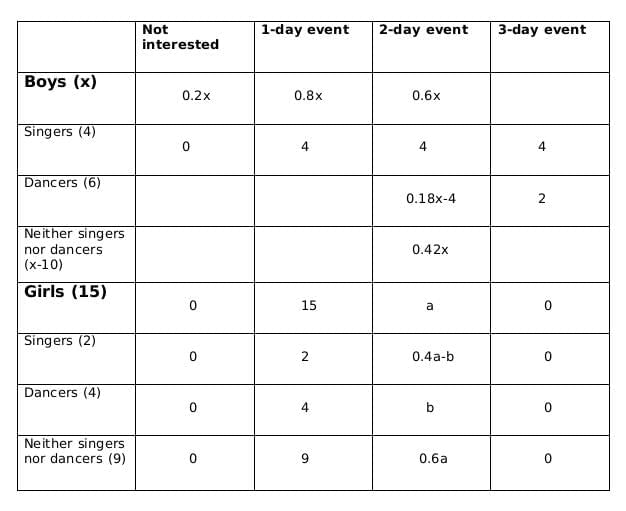
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
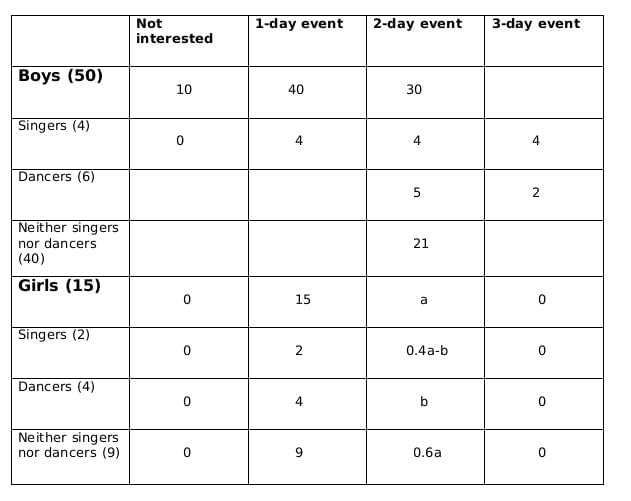
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a = 5 then b =1.
Q3: What fraction of the class are interested in attending a 2-day event?
(a) 7/10
(b) 7/13
(c) 9/13
(d) 2/3
View Answer Ans: (b)
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
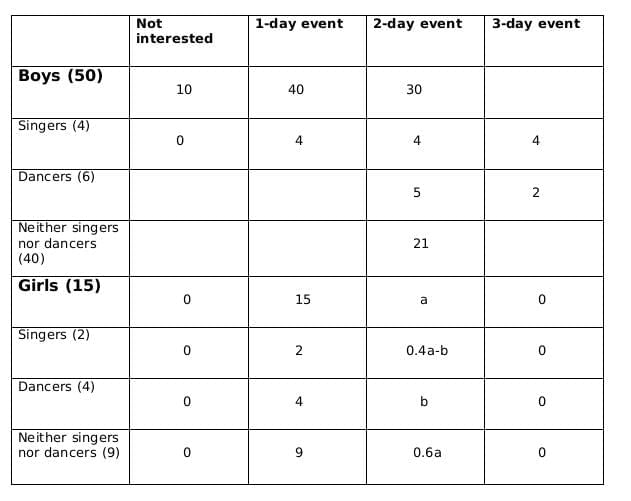
Total students interested in 2-day event = 30+5 = 35
Total students = 15 + 50 = 65
Fraction = 35/65 = 7/13
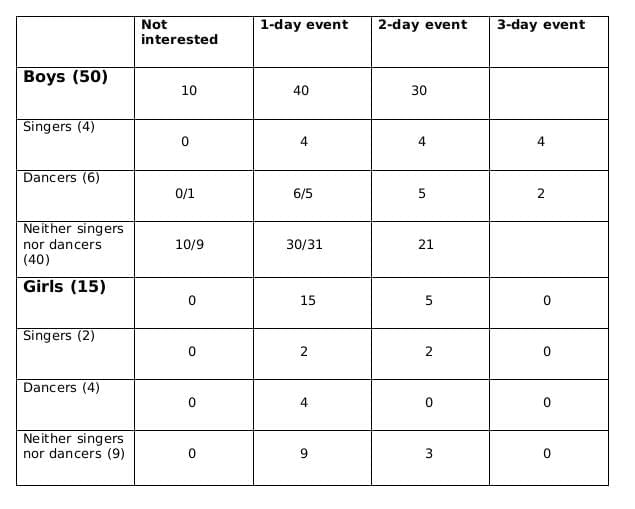
Q4: What BEST can be concluded about the number of male dancers who are interested in attending a 1-day event?
(a) 5 or 6
(b) 6
(c) 5
(d) 4 or 6
View Answer Ans: (a)
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
Now we fill the above table, using statements 1 and 2, we get the following table
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a = 5 then b = 1.
Q5: How many female dancers are interested in attending a 2-day event?
(a) 2
(b) 1
(c) 0
(d) Cannot be determined
View Answer Ans: (c)
No. of girls = 15
Let the no. of boys be x
No. of singers = 6
No of boys who are singers = 4
Therefore, no of girls who are singers = 2
No of dancers = 10
No of boys who are dancers = 6
Therefore, no. of girls who are dancers = 4
No. of boys who are neither singers nor dancers = x-10
No. of girls who are neither singers nor dancers = 9
Now we fill the above table, using statements 1 and 2, we get the following table
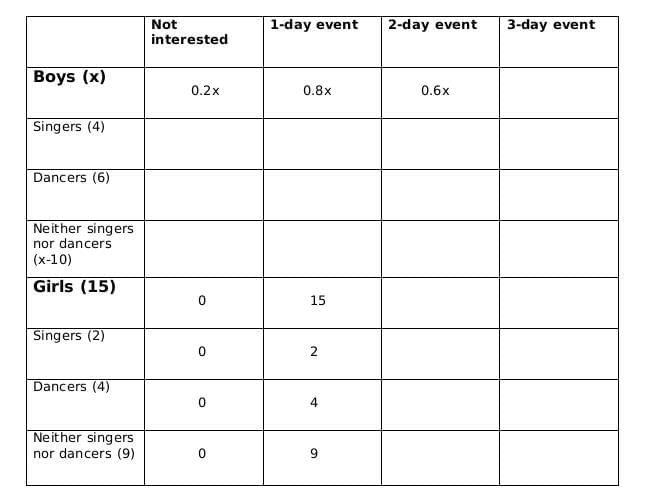
Let the number of girls who are interested in attending a 2-day event be a and the number of girls who are dancers and are interested in 2-day event be b.
Now using statements 3 and 4, we get
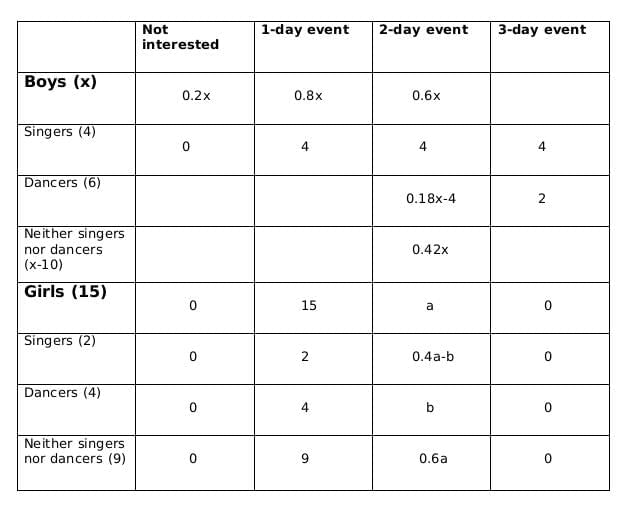
2 ≤ 0.18x − 4 ≤ 6
6 ≤ 0.18x ≤ 10
0.18x should be integer for which x should be a multiple of 50, and 0.18x lies between 6 and 10; therefore, the only possible value of x is 50.
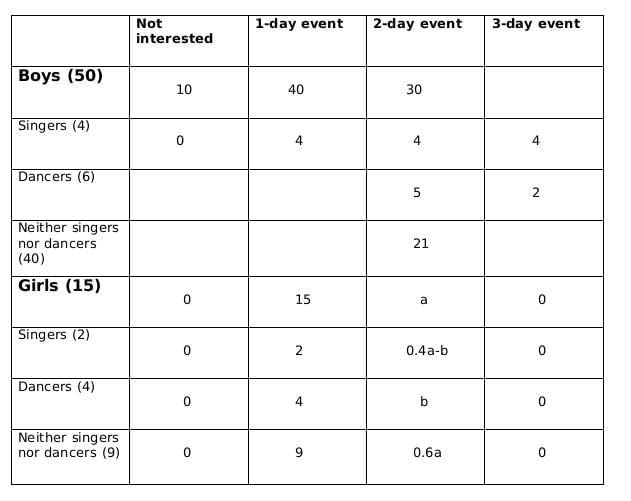
From statement 5, we can say that,
4+ 0.4a - b = 5+b +1
or, 0.4a = 2+2b
or, a = 5(1+b)
a should be a multiple of 5 as b is a whole number. So possible values of a can be 5, 10 or 15. Now, as the maximum value of b can be 4 and the maximum value of 0.4a-b can be 2, so the only possible value of a satisfying the conditions above is 5. If a= 5 then b=1.
|
102 videos|123 docs|121 tests
|
FAQs on Practice Question - 12 (Venn Diagram) - 100 DILR Questions for CAT Preparation
| 1. What is a Venn diagram, and how is it used in problem-solving? |  |
| 2. How can Venn diagrams be applied to solve problems in competitive exams? | |
| 3. What types of questions can be expected in exams that involve Venn diagrams? | |
| 4. What are some common mistakes to avoid when interpreting Venn diagrams? | |
| 5. Can Venn diagrams be used beyond mathematics, and if so, how? | |
past year papers
,study material
,Practice Question - 12 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,Practice Question - 12 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,Sample Paper
,mock tests for examination
,Objective type Questions
,Practice Question - 12 (Venn Diagram) | 100 DILR Questions for CAT Preparation
,Exam
,Previous Year Questions with Solutions
,video lectures
,Summary
,Extra Questions
,MCQs
,ppt
,practice quizzes
,Important questions
,Free
,Semester Notes
,Viva Questions
,shortcuts and tricks
;
Practice Question - 12 (Venn Diagram) Free PDF Download
Importance of Practice Question - 12 (Venn Diagram)
Practice Question - 12 (Venn Diagram) Notes
Practice Question - 12 (Venn Diagram) CAT Questions
Study Practice Question - 12 (Venn Diagram) on the App
|
© EduRev
|
Education Revolution
|
|
