Unit Test (Solutions): Animal Jumps | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each
Q1: Which of the following is a prime number? (1 Mark)
(a) 9
(b) 11
(c) 15
(d) 21
Ans: (b) 11
Prime numbers have exactly 2 factors: 1 and the number itself.
11 has only 1 and 11 as factors.
Q2: The least common multiple (LCM) of 4 and 6 is: (1 Mark)
(a) 8
(b) 10
(c) 12
(d) 14
Ans: (c) 12
Multiples of 4 → 4, 8, 12, 16…
Multiples of 6 → 6, 12, 18…
Smallest common multiple = 12.
Q3: Which of the following is NOT a factor of 30? (1 Mark)
(a) 2
(b) 3
(c) 5
(d) 7
Ans: (d) 7
Factors of 30 → 1, 2, 3, 5, 6, 10, 15, 30
7 does not divide 30.
Q4: Which of the following numbers is both a factor and a multiple of 9? (1 Mark)
(a) 1
(b) 3
(c) 9
(d) 18
Ans: (c) 9
Factor of 9 means it divides 9 exactly.
Multiple of 9 means it is in 9, 18, 27,…
Only 9 is both.
Q5: A number that has exactly two factors is called a: (1 Mark)
(a) Prime number
(b) Composite number
(c) Even number
(d) Odd number
Ans: (a) Prime number
- Numbers with only 2 factors (1 and itself) are prime numbers.
Q6: True or False (2 Marks)
(i) 36 is a multiple of 9.
Ans: True
The first ten multiples of 9 are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90.
(ii) 6 is the least non-zero multiple of 6.
Ans: True
In this question, the number is 6.
We know that, multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54 and so on.
By observing above multiples, it is clear that, 6 is the least non-zero multiple of 6.
So, the least non-zero multiple of 6 is 6.
(iii) 1 is the multiple of 5.
Ans: True
Yes, every whole number is a multiple of 1.
Q7: Fill in the Blanks (2 Marks)
(i) The first six multiples of 4 are ____, ____, ____, ____, ____, and ____.
Ans: 4, 8, 12, 16, 20, 24
Multiples of 4 obtained by multiplying 4 by counting numbers 1 through 6.
(ii) A number divisible by both 3 and 5 is a multiple of ____.
Ans: 15
3 × 5 = 15, a number divisible by both 3 and 5.
(iii) The number 17 is ____ because it has only two factors.
Ans: prime
Prime numbers have only two factors: 1 and the number itself.
(iv) The smallest whole number is ____.
Ans: 0
Whole numbers start from 0.
(v) The common factors of 12 and 18 are ____, ____, and ____.
Ans: 1, 2, 3, 6
Factors of 12: 1, 2, 3, 4, 6, 12. Factors of 18: 1, 2, 3, 6, 9, 18. Common factors are 1, 2, 3, 6.
Q8: Find the common multiples of 3 and 5. (2 Marks)
Solution: Multiples of 3 – 3, 6, 9, 12, 15, 18, 21
Multiples of 5 – 5, 10, 15, 20, 25
15 is a common multiple of 3 and 5.
Indeed, 15 is the least common multiple (LCM) of 3 and 5.
Q9: Identify the common factors of 20 and 35.? (3 Marks)
Solution: Find the factors of each number and then determine which ones are common.
Factors of 20: 1, 2, 4, 5, 10, 20.
Factors of 35: 1, 5, 7, 35.
Common factors: 1 and 5.
Note: We first find all factors of each number and then identify those that appear in both lists. These common factors are the ones that divide both numbers evenly.
Q10: Find out all the factors of 24. (3 Marks)
Solution: 24 ÷ 1 = 24 24 ÷ 2 = 12 24 ÷ 3 = 8
24 ÷ 4 = 6 24 ÷ 6 = 4 24 ÷ 8 = 3
24 ÷ 12 = 2 24 ÷ 24 = 1
1, 2, 3, 4, 6, 8, 12 and 24 are factors of 24 as they divide 24 exactly. Hence, factors are also divisors of a number. When you divide one number by another and there is no remainder, the divisor and the quotient are factors of the fi rst number.
Q11: Find all the factors of 36 using the division method. (3 Marks)
Solution: We start by dividing 36 by the smallest prime number, which is 2.
We find that 36 ÷ 2 = 18. Since 18 is still divisible by 2, we continue dividing: 18 ÷ 2 = 9. Finally, 9 is not divisible by 2, so we move to the next smallest prime number, which is 3. Dividing 9 by 3, we get 9 ÷ 3 = 3. Since 3 is a prime number, we stop here.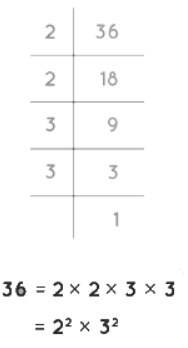
Q12: There are 24 boys and 36 girls in a class. The teacher wants to divide them into groups so that each group has the same number of boys and the same number of girls. What is the greatest number of groups that can be made? (5 Marks)
Solution:
We need to find the HCF of 24 and 36.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
HCF = 12
Answer: The teacher can make 12 groups.
Q13: A bell rings every 20 minutes and another bell rings every 30 minutes. If they both ring together at 9:00 a.m., at what time will they ring together again? (5 Marks)
Solution:
We need the LCM of 20 and 30.
Multiples of 20: 20, 40, 60, 80, 100, 120
Multiples of 30: 30, 60, 90, 120
LCM = 60 minutes
So, they will ring together after 60 minutes = 1 hour.
9:00 a.m. + 1 hour = 10:00 a.m.
Answer: The bells will ring together again at 10:00 a.m.
|
35 videos|276 docs|7 tests
|
FAQs on Unit Test (Solutions): Animal Jumps - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are the different types of animals that can jump and what are their unique jumping abilities? |  |
| 2. How do the jumping mechanics of animals differ from one species to another? |  |
| 3. What role does jumping play in the survival of animals in the wild? |  |
| 4. Are there any specific adaptations that enhance an animal's jumping ability? |  |
| 5. How do environmental factors influence the jumping abilities of animals? |  |





















