Practice Question - 60 (Quant Based) | 100 DILR Questions for CAT Preparation PDF Download
Odsville has five firms - Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores. The table below provides partial information about the five firms.
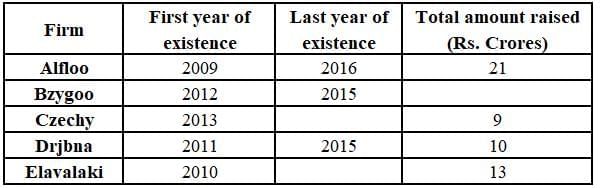
Q1: For which firm(s) can the amounts raised by them be concluded with certainty in each year?
(a) Only Bzygoo and Czechy and Drjbna
(b) Only Czechy and Drjbna
(c) Only Drjbna
(d) Only Czechy
 View Answer
View Answer 
Ans: (b)
In this set, we are told that the amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down and no firm raised the same amount of money in two consecutive years.
The increase or decrease can be ±1 or ±2. ⇒ (1)
We are also told that each firm raised Rs. 1 crore in its first and last year of existence
Consider A:
It raised money for 8 years
⇒ The raising pattern looks like follows:
1, a, b, c, d, e, f, 1 => where a, b, c,..,, f are the unknown amounts raised.
Also a + b + c + d + e + f = 21 - 2 = 19.
We can observe that 19/6 is slightly greater than 3 => The average amount raised should be around 3.
If a = 3 and f = 3 ⇒ b + c + d + e = 13 (not possible) as the minimum case would be (4, 5, 6, 4) ⇒ Not possible.
If a = 3 and f = 2 ⇒ b + c + d + e = 14 (not possible) as the minimum case would be (4, 5, 4, 3) ⇒ Not possible.
⇒ a = 2 and f = 2 ⇒ b + c + d + e = 15 the minimum case is (3, 4, 5, 3) or (3, 5, 4, 3) which gives a sum of 15.
So, the possible cases for A are: Consider B:
Consider B:
The patterns looks as follows:
1, a, b, 1
If a = 2, b has to be equal to 3 to satisfy (1)
if a = 3, b has to be equal to 2 to satisfy (1)
⇒ The possible cases for B are: Consider C:
Consider C:
The pattern looks as follows:
1, ..., 1
Let us assume there are 2 gaps between ⇒ a + b = 7 (Not possible) as maximum case would be 1, 3, 2, 1
Let us assume there are 3 gaps between ⇒ a + b + c = 7, the minimum case possible is 1, 2, 3, 2, 1 ⇒ Satisfies.
Now, if there are 4 gaps ⇒ a + b + c + d = 7 ⇒ The average value is 7/4 which is less than 2 ⇒ Not possible.
⇒ The possible cases for C are:
Consider D:
The pattern looks as follows:
1, a, b, c, 1
⇒ a + b + c = 8
When a = 2 and c = 2 => b = 4 => 2, 4, 2 => Satisfies.
When a = 2 and c = 3, b should be 3 (Not satisfying (1))
When a = 3 and c = 3, b should be 2 (Not satisfying (1))
⇒ The possible cases for D are: Consider E:
Consider E:
The pattern looks as follows:
1,.....,1
For 1 or 2 gaps, we can't get a sum of 11.
Assume 3 gaps ⇒ a + b + c = 11, the maximum case is 3, 5, 3 ⇒ Satisfies.
Now, assume 4 gaps
⇒ a + b + c + d = 11, the minimum case is 2, 3, 4, 2 or 2, 4, 3, 2 which satisfies (1) and 2 + 3 + 4 + 2 = 11.
⇒ The possible cases for E are:

In summary, the possible cases for all 5 companies is: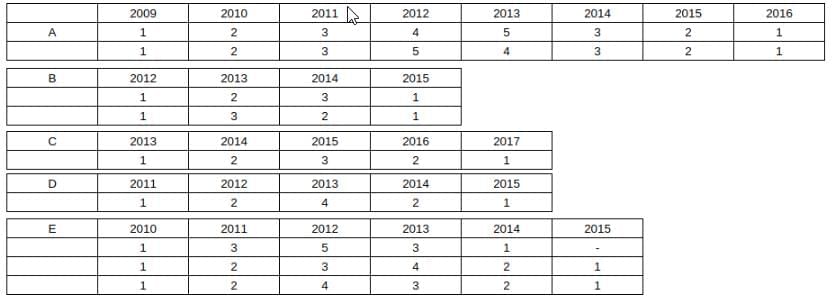
We see that only for C and D, we can conclude the amounts raised with certainty.
Q2: What best can be concluded about the total amount of money raised in 2015?
(a) It is either Rs. 7 crores or Rs. 8 crores or Rs. 9 crores.
(b) It is exactly Rs. 8 crores.
(c) It is either Rs. 7 crores or Rs. 8 crores.
(d) It is either Rs. 8 crores or Rs. 9 crores.
 View Answer
View Answer 
Ans: (c)
In this set, we are told that the amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down and no firm raised the same amount of money in two consecutive years.
The increase or decrease can be ±1 or ±2. ⇒ (1)
We are also told that each firm raised Rs. 1 crore in its first and last year of existence
Consider A:
It raised money for 8 years
⇒ The raising pattern looks like follows:
1, a, b, c, d, e, f, 1 => where a, b, c,..,, f are the unknown amounts raised.
Also a + b + c + d + e + f = 21 - 2 = 19.
We can observe that 19/6 is slightly greater than 3 => The average amount raised should be around 3.
If a = 3 and f = 3 ⇒ b + c + d + e = 13 (not possible) as the minimum case would be (4, 5, 6, 4) ⇒ Not possible.
If a = 3 and f = 2 ⇒ b + c + d + e = 14 (not possible) as the minimum case would be (4, 5, 4, 3) ⇒ Not possible.
⇒ a = 2 and f = 2 ⇒ b + c + d + e = 15 the minimum case is (3, 4, 5, 3) or (3, 5, 4, 3) which gives a sum of 15.
So, the possible cases for A are: Consider B:
Consider B:
The patterns looks as follows:
1, a, b, 1
If a = 2, b has to be equal to 3 to satisfy (1)
if a = 3, b has to be equal to 2 to satisfy (1)
⇒ The possible cases for B are: Consider C:
Consider C:
The pattern looks as follows:
1, ..., 1
Let us assume there are 2 gaps between ⇒ a + b = 7 (Not possible) as maximum case would be 1, 3, 2, 1
Let us assume there are 3 gaps between ⇒ a + b + c = 7, the minimum case possible is 1, 2, 3, 2, 1 ⇒ Satisfies.
Now, if there are 4 gaps ⇒ a + b + c + d = 7 ⇒ The average value is 7/4 which is less than 2 ⇒ Not possible.
⇒ The possible cases for C are:
Consider D:
The pattern looks as follows:
1, a, b, c, 1
⇒ a + b + c = 8
When a = 2 and c = 2 => b = 4 => 2, 4, 2 => Satisfies.
When a = 2 and c = 3, b should be 3 (Not satisfying (1))
When a = 3 and c = 3, b should be 2 (Not satisfying (1))
⇒ The possible cases for D are: Consider E:
Consider E:
The pattern looks as follows:
1,.....,1
For 1 or 2 gaps, we can't get a sum of 11.
Assume 3 gaps ⇒ a + b + c = 11, the maximum case is 3, 5, 3 ⇒ Satisfies.
Now, assume 4 gaps
⇒ a + b + c + d = 11, the minimum case is 2, 3, 4, 2 or 2, 4, 3, 2 which satisfies (1) and 2 + 3 + 4 + 2 = 11.
⇒ The possible cases for E are:

In summary, the possible cases for all 5 companies is: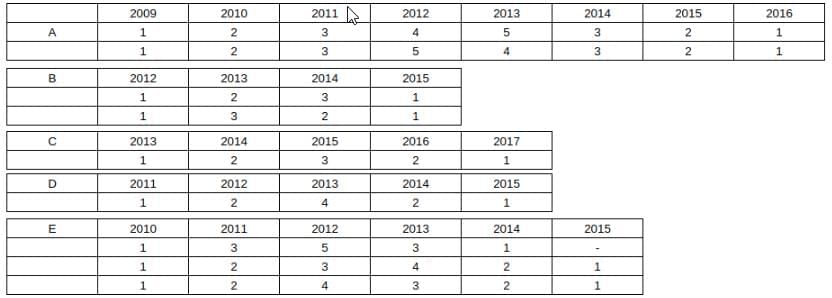
Money raised in 2015 is 2 + 1 + 3 + 1 + 0/1 = 7 or 8.
Q3: What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
 View Answer
View Answer 
Ans: 17
In this set, we are told that the amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down and no firm raised the same amount of money in two consecutive years.
The increase or decrease can be ±1 or ±2. ⇒ (1)
We are also told that each firm raised Rs. 1 crore in its first and last year of existence
Consider A:
It raised money for 8 years
⇒ The raising pattern looks like follows:
1, a, b, c, d, e, f, 1 => where a, b, c,..,, f are the unknown amounts raised.
Also a + b + c + d + e + f = 21 - 2 = 19.
We can observe that 19/6 is slightly greater than 3 => The average amount raised should be around 3.
If a = 3 and f = 3 ⇒ b + c + d + e = 13 (not possible) as the minimum case would be (4, 5, 6, 4) ⇒ Not possible.
If a = 3 and f = 2 ⇒ b + c + d + e = 14 (not possible) as the minimum case would be (4, 5, 4, 3) ⇒ Not possible.
⇒ a = 2 and f = 2 ⇒ b + c + d + e = 15 the minimum case is (3, 4, 5, 3) or (3, 5, 4, 3) which gives a sum of 15.
So, the possible cases for A are: Consider B:
Consider B:
The patterns looks as follows:
1, a, b, 1
If a = 2, b has to be equal to 3 to satisfy (1)
if a = 3, b has to be equal to 2 to satisfy (1)
⇒ The possible cases for B are: Consider C:
Consider C:
The pattern looks as follows:
1, ..., 1
Let us assume there are 2 gaps between ⇒ a + b = 7 (Not possible) as maximum case would be 1, 3, 2, 1
Let us assume there are 3 gaps between ⇒ a + b + c = 7, the minimum case possible is 1, 2, 3, 2, 1 ⇒ Satisfies.
Now, if there are 4 gaps ⇒ a + b + c + d = 7 ⇒ The average value is 7/4 which is less than 2 ⇒ Not possible.
⇒ The possible cases for C are:
Consider D:
The pattern looks as follows:
1, a, b, c, 1
⇒ a + b + c = 8
When a = 2 and c = 2 => b = 4 => 2, 4, 2 => Satisfies.
When a = 2 and c = 3, b should be 3 (Not satisfying (1))
When a = 3 and c = 3, b should be 2 (Not satisfying (1))
⇒ The possible cases for D are: Consider E:
Consider E:
The pattern looks as follows:
1,.....,1
For 1 or 2 gaps, we can't get a sum of 11.
Assume 3 gaps ⇒ a + b + c = 11, the maximum case is 3, 5, 3 ⇒ Satisfies.
Now, assume 4 gaps
⇒ a + b + c + d = 11, the minimum case is 2, 3, 4, 2 or 2, 4, 3, 2 which satisfies (1) and 2 + 3 + 4 + 2 = 11.
⇒ The possible cases for E are:

In summary, the possible cases for all 5 companies is: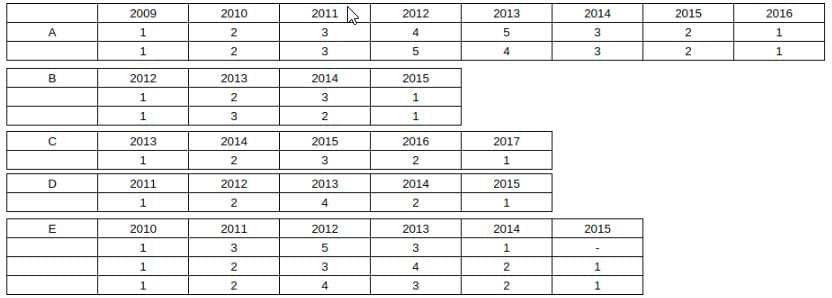
Maximum money raised in 2013 is 5 + 3 + 1 + 4 + 4 = 17.
Q4: If Elavalaki raised Rs. 3 crores in 2013, then what is the smallest possible total amount of money (in Rs. crores) that could have been raised by all the companies in 2012?
(a) 12
(b) 9
(c) 11
(d) 10
 View Answer
View Answer 
Ans: (c)
In this set, we are told that the amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down and no firm raised the same amount of money in two consecutive years.
The increase or decrease can be ±1 or ±2. ⇒ (1)
We are also told that each firm raised Rs. 1 crore in its first and last year of existence
Consider A:
It raised money for 8 years
⇒ The raising pattern looks like follows:
1, a, b, c, d, e, f, 1 => where a, b, c,..,, f are the unknown amounts raised.
Also a + b + c + d + e + f = 21 - 2 = 19.
We can observe that 19/6 is slightly greater than 3 => The average amount raised should be around 3.
If a = 3 and f = 3 ⇒ b + c + d + e = 13 (not possible) as the minimum case would be (4, 5, 6, 4) ⇒ Not possible.
If a = 3 and f = 2 ⇒ b + c + d + e = 14 (not possible) as the minimum case would be (4, 5, 4, 3) ⇒ Not possible.
⇒ a = 2 and f = 2 ⇒ b + c + d + e = 15 the minimum case is (3, 4, 5, 3) or (3, 5, 4, 3) which gives a sum of 15.
So, the possible cases for A are: Consider B:
Consider B:
The patterns looks as follows:
1, a, b, 1
If a = 2, b has to be equal to 3 to satisfy (1)
if a = 3, b has to be equal to 2 to satisfy (1)
⇒ The possible cases for B are: Consider C:
Consider C:
The pattern looks as follows:
1, ..., 1
Let us assume there are 2 gaps between ⇒ a + b = 7 (Not possible) as maximum case would be 1, 3, 2, 1
Let us assume there are 3 gaps between ⇒ a + b + c = 7, the minimum case possible is 1, 2, 3, 2, 1 ⇒ Satisfies.
Now, if there are 4 gaps ⇒ a + b + c + d = 7 ⇒ The average value is 7/4 which is less than 2 ⇒ Not possible.
⇒ The possible cases for C are:
Consider D:
The pattern looks as follows:
1, a, b, c, 1
⇒ a + b + c = 8
When a = 2 and c = 2 => b = 4 => 2, 4, 2 => Satisfies.
When a = 2 and c = 3, b should be 3 (Not satisfying (1))
When a = 3 and c = 3, b should be 2 (Not satisfying (1))
⇒ The possible cases for D are: Consider E:
Consider E:
The pattern looks as follows:
1,.....,1
For 1 or 2 gaps, we can't get a sum of 11.
Assume 3 gaps ⇒ a + b + c = 11, the maximum case is 3, 5, 3 ⇒ Satisfies.
Now, assume 4 gaps
⇒ a + b + c + d = 11, the minimum case is 2, 3, 4, 2 or 2, 4, 3, 2 which satisfies (1) and 2 + 3 + 4 + 2 = 11.
⇒ The possible cases for E are:

In summary, the possible cases for all 5 companies is: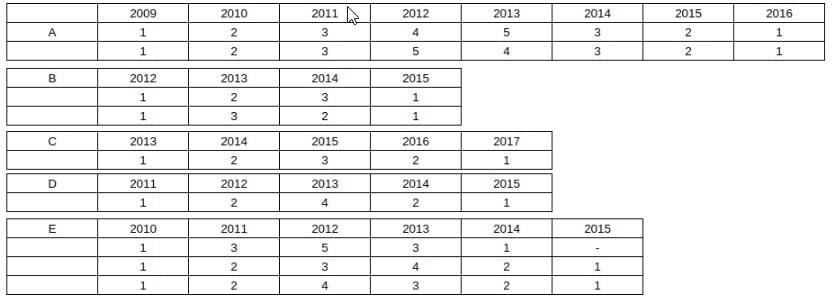
Given that E raised 3 in 2013 ⇒ in 2012 he could have raised a minimum of 4 crores.
⇒ Minimum amount is 4 + 1 + 0 + 2 + 4 = 11.
Q5: If the total amount of money raised in 2014 is Rs. 12 crores, then which of the following is not possible?
(a) Bzygoo raised the same amount of money as Elavalaki in 2013.
(b) Alfloo raised the same amount of money as Drjbna in 2013.
(c) Alfloo raised the same amount of money as Bzygoo in 2014.
(d) Bzygoo raised more money than Elavalaki in 2014.
 View Answer
View Answer 
Ans: (a)
In this set, we are told that the amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down and no firm raised the same amount of money in two consecutive years.
The increase or decrease can be ±1 or ±2. ⇒ (1)
We are also told that each firm raised Rs. 1 crore in its first and last year of existence
Consider A:
It raised money for 8 years
⇒ The raising pattern looks like follows:
1, a, b, c, d, e, f, 1 => where a, b, c,..,, f are the unknown amounts raised.
Also a + b + c + d + e + f = 21 - 2 = 19.
We can observe that 19/6 is slightly greater than 3 => The average amount raised should be around 3.
If a = 3 and f = 3 ⇒ b + c + d + e = 13 (not possible) as the minimum case would be (4, 5, 6, 4) ⇒ Not possible.
If a = 3 and f = 2 ⇒ b + c + d + e = 14 (not possible) as the minimum case would be (4, 5, 4, 3) ⇒ Not possible.
⇒ a = 2 and f = 2 ⇒ b + c + d + e = 15 the minimum case is (3, 4, 5, 3) or (3, 5, 4, 3) which gives a sum of 15.
So, the possible cases for A are: Consider B:
Consider B:
The patterns looks as follows:
1, a, b, 1
If a = 2, b has to be equal to 3 to satisfy (1)
if a = 3, b has to be equal to 2 to satisfy (1)
⇒ The possible cases for B are: Consider C:
Consider C:
The pattern looks as follows:
1, ..., 1
Let us assume there are 2 gaps between ⇒ a + b = 7 (Not possible) as maximum case would be 1, 3, 2, 1
Let us assume there are 3 gaps between ⇒ a + b + c = 7, the minimum case possible is 1, 2, 3, 2, 1 ⇒ Satisfies.
Now, if there are 4 gaps ⇒ a + b + c + d = 7 ⇒ The average value is 7/4 which is less than 2 ⇒ Not possible.
⇒ The possible cases for C are:
Consider D:
The pattern looks as follows:
1, a, b, c, 1
⇒ a + b + c = 8
When a = 2 and c = 2 => b = 4 => 2, 4, 2 => Satisfies.
When a = 2 and c = 3, b should be 3 (Not satisfying (1))
When a = 3 and c = 3, b should be 2 (Not satisfying (1))
⇒ The possible cases for D are: Consider E:
Consider E:
The pattern looks as follows:
1,.....,1
For 1 or 2 gaps, we can't get a sum of 11.
Assume 3 gaps ⇒ a + b + c = 11, the maximum case is 3, 5, 3 ⇒ Satisfies.
Now, assume 4 gaps
⇒ a + b + c + d = 11, the minimum case is 2, 3, 4, 2 or 2, 4, 3, 2 which satisfies (1) and 2 + 3 + 4 + 2 = 11.
⇒ The possible cases for E are:

In summary, the possible cases for all 5 companies is: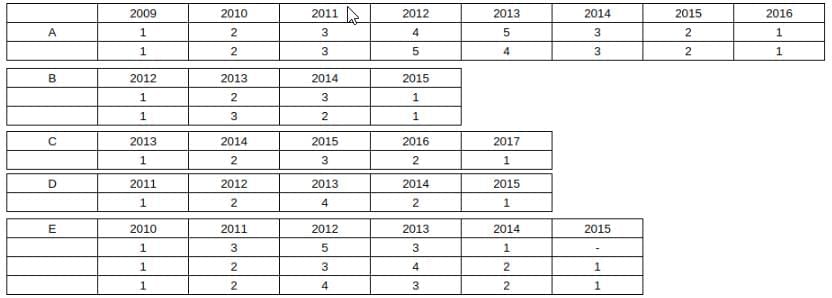 Given that total amount raised in 2014 is 12
Given that total amount raised in 2014 is 12
⇒ 3 + 3/2 + 2 + 2 + 1/2 = 12 ⇒
⇒ possible case is 3 + 3 + 2 + 2 + 2 = 12.
A) In 2013, B raised 2 crores and E also raised 3/4 crores ⇒ Not Possible.
B) In 2013, A could have raised 5/4 and D raised 4⇒ Possible.
C) In 2014, A raised 3 and B raised 3 ⇒ Possible.
D) In 2014, B raised 3 where as E raised 2 ⇒ 3 > 2 ⇒ Possible.
|
102 videos|123 docs|121 tests
|
FAQs on Practice Question - 60 (Quant Based) - 100 DILR Questions for CAT Preparation
| 1. What is the format of the Quantitative Ability section in the CAT exam? |  |
| 2. How can candidates effectively prepare for the Quantitative Ability section of the CAT? |  |
| 3. Are calculators allowed during the CAT exam? |  |
| 4. What is the scoring pattern for the Quantitative Ability section in the CAT? |  |
| 5. What are some common topics covered in the Quantitative Ability section of the CAT exam? |  |















