Practice Question - 65 (Tables) | 100 DILR Questions for CAT Preparation PDF Download
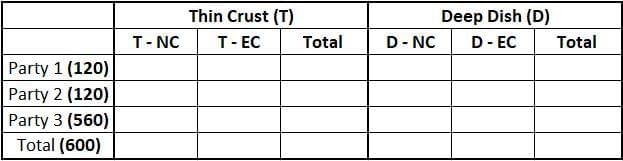
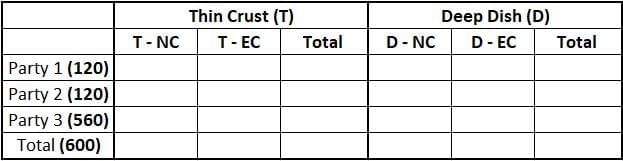
Funky Pizzeria was required to supply pizzas to three different parties. The total number of pizzas it had to deliver was 800, 70% of which were to be delivered to Party 3 and the rest equally divided between Party 1 and Party 2.
Pizzas could be of Thin Crust (T) or Deep Dish (D) variety and come in either Normal Cheese (NC) or Extra Cheese (EC) versions. Hence, there are four types of pizzas: T-NC, T-EC, D-NC and D-EC. Partial information about proportions of T and NC pizzas ordered by the three parties is given below:
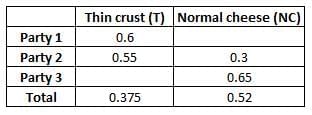
Q1: How many Thin Crust pizzas were to be delivered to Party 3?
(a) 398
(b) 162
(c) 96
(d) 364
View Answer 
Ans: (b)
We are given that Party 3 received 70% of total pizzas,therefore, number of pizzas received by Party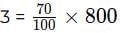 
Remaining 240 pizzas are equally divided among party 1 and party 2 hence we can say that each of Party 1 and Party 2 received 120 pizzas.
We know that all of the pizza can be classified into a total of 4 types. Hence, on drawing a table which can accommodate all of the cases:
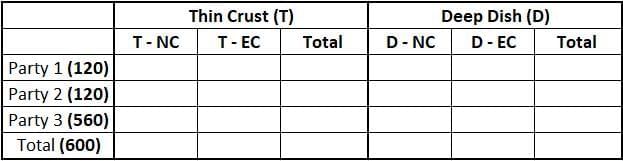
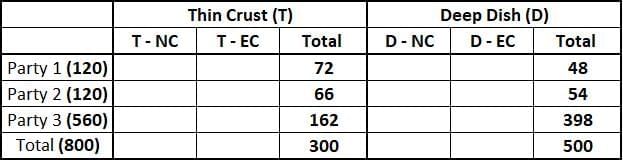
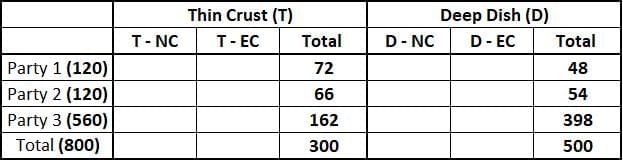
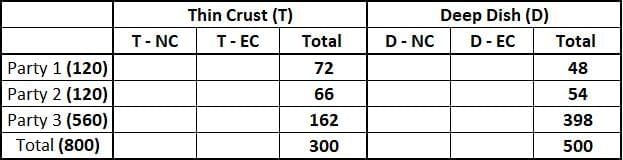
Total number of Thin Crust pizzas = 0.375*800 = 300. Therefore, total number of Deep Dish pizzas = 800 - 300 = 500.
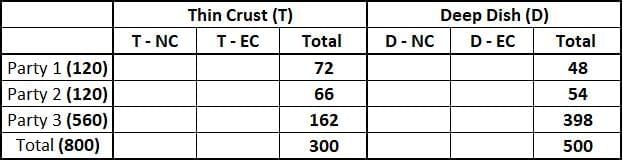
Out of 120 pizzas that Party 1 received, 60% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 1 = 0.6*120 = 72. Consequently Party 1, must have received 42 Deep Dish type pizzas.
Out of 120 pizzas that Party 2 received, 55% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 2 = 0.55*120 = 66. Consequently Party 1, must have received 54 Deep Dish type pizzas.
Therefore, total number of Thin Crust pizzas ordered by Party 3 = Total Thin Crust pizzas ordered - Thin Crust pizzas ordered by Party 1 - Thin Crust pizzas ordered by Party 2
⇒ 300 - 72 - 66 = 162
Hence number of Deep Dish type of pizzas order by Party 3 = 560 - 162 = 398
No, of Thin Crust Pizzas delivered to party 3 is 162. Hence, option (b) is the correct answer.
Q2: How many Normal Cheese pizzas were required to be delivered to Party 1?
(a) 104
(b) 84
(c) 16
(d) 196
View Answer We are given that Party 3 received 70% of total pizzas,therefore, number of pizzas received by Party
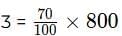
Remaining 240 pizzas are equally divided among party 1 and party 2 hence we can say that each of Party 1 and Party 2 received 120 pizzas.
We know that all of the pizza can be classified into a total of 4 types. Hence, on drawing a table which can accommodate all of the cases:
Total number of Thin Crust pizzas = 0.375*800 = 300. Therefore, total number of Deep Dish pizzas = 800 - 300 = 500.
Out of 120 pizzas that Party 1 received, 60% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 1 = 0.6*120 = 72. Consequently Party 1, must have received 42 Deep Dish type pizzas.
Out of 120 pizzas that Party 2 received, 55% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 2 = 0.55*120 = 66. Consequently Party 1, must have received 54 Deep Dish type pizzas.
Therefore, total number of Thin Crust pizzas ordered by Party 3 = Total Thin Crust pizzas ordered - Thin Crust pizzas ordered by Party 1 - Thin Crust pizzas ordered by Party 2
⇒ 300 - 72 - 66 = 162
Hence number of Deep Dish type of pizzas order by Party 3 = 560 - 162 = 398
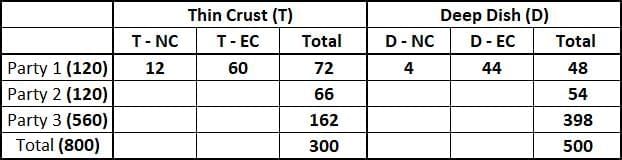
Total number of Normal Cheese pizzas require to be delivered = 0.52*800 = 416
Number of Normal Cheese pizzas require to be delivered to Party 2 = 0.3*120 = 36
Number of Normal Cheese pizzas require to be delivered to Party 3 = 0.65*560 = 364
Therefore, total number of Normal Cheese pizzas require to be delivered to Party 1 = Total Normal Cheese pizzas to be delivered - Normal Cheese pizzas require to be delivered to Party 2 - Normal Cheese pizzas require to be delivered to Party 3
⇒ 416 - 36 - 364 = 16
Hence, option (c) is the correct answer.
Q3: For Party 2, if 50% of the Normal Cheese pizzas were of Thin Crust variety, what was the difference between the numbers of T-EC and D-EC pizzas to be delivered to Party 2?
(a) 18
(b) 12
(c) 30
(d) 24
View Answer Ans: (b)
We are given that Party 3 received 70% of total pizzas,therefore, number of pizzas received by Party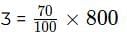 
Remaining 240 pizzas are equally divided among party 1 and party 2 hence we can say that each of Party 1 and Party 2 received 120 pizzas.
We know that all of the pizza can be classified into a total of 4 types. Hence, on drawing a table which can accommodate all of the cases:
Total number of Thin Crust pizzas = 0.375*800 = 300. Therefore, total number of Deep Dish pizzas = 800 - 300 = 500.
Out of 120 pizzas that Party 1 received, 60% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 1 = 0.6*120 = 72. Consequently Party 1, must have received 42 Deep Dish type pizzas.
Out of 120 pizzas that Party 2 received, 55% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 2 = 0.55*120 = 66. Consequently Party 1, must have received 54 Deep Dish type pizzas.
Therefore, total number of Thin Crust pizzas ordered by Party 3 = Total Thin Crust pizzas ordered - Thin Crust pizzas ordered by Party 1 - Thin Crust pizzas ordered by Party 2
⇒ 300 - 72 - 66 = 162
Hence number of Deep Dish type of pizzas order by Party 3 = 560 - 162 = 398
Number of Normal Cheese pizzas require to be delivered to Party 2 = 0.3*120 = 36
It is given that 50% of these Normal Cheese pizzas were of Thin Crust variety, then We can say that remaining 50% were of Deep Dish variety. We can find out each of 4 types of pizzas require to be delivered to Party 2.
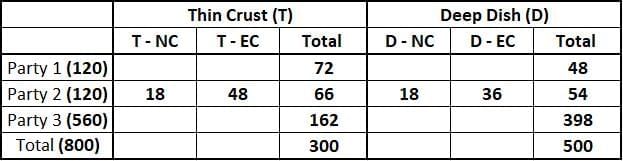
Hence, the difference between the numbers of T-EC and D-EC pizzas to be delivered to Party 2 = 48 - 36 = 12
Therefore, option (b) is the correct answer.
Q4: Suppose that a T-NC pizza cost as much as a D-NC pizza, but 3/5th of the price of a D-EC pizza.A D-EC pizza costs Rs. 50 more than a T-EC pizza, and the latter costs Rs. 500.
If 25% of the Normal Cheese pizzas delivered to Party 1 were of Deep Dish variety, what was the total bill for Party 1?
(a) Rs. 59480
(b) Rs. 59840
(c) Rs. 42520
(d) Rs. 45240
View Answer Ans: (a)
We are given that Party 3 received 70% of total pizzas,therefore, number of pizzas received by Party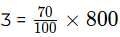 
Remaining 240 pizzas are equally divided among party 1 and party 2 hence we can say that each of Party 1 and Party 2 received 120 pizzas.
We know that all of the pizza can be classified into a total of 4 types. Hence, on drawing a table which can accommodate all of the cases:
Total number of Thin Crust pizzas = 0.375*800 = 300. Therefore, total number of Deep Dish pizzas = 800 - 300 = 500.
Out of 120 pizzas that Party 1 received, 60% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 1 = 0.6*120 = 72. Consequently Party 1, must have received 42 Deep Dish type pizzas.
Out of 120 pizzas that Party 2 received, 55% were of Thin Crust type hence, total number of Thin Crust pizza received by Party 2 = 0.55*120 = 66. Consequently Party 1, must have received 54 Deep Dish type pizzas.
Therefore, total number of Thin Crust pizzas ordered by Party 3 = Total Thin Crust pizzas ordered - Thin Crust pizzas ordered by Party 1 - Thin Crust pizzas ordered by Party 2
⇒ 300 - 72 - 66 = 162
Hence number of Deep Dish type of pizzas order by Party 3 = 560 - 162 = 398
Total number of Normal Cheese pizzas require to be delivered = 0.52*800 = 416
Number of Normal Cheese pizzas require to be delivered to Party 2 = 0.3*120 = 36
Number of Normal Cheese pizzas require to be delivered to Party 3 = 0.65*560 = 364
Therefore, total number of Normal Cheese pizzas require to be delivered to Party 1 = Total Normal Cheese pizzas to be delivered - Normal Cheese pizzas require to be delivered to Party 2 - Normal Cheese pizzas require to be delivered to Party 3
⇒ 416 - 36 - 364 = 16
It is given that 25% of these 16 Normal Cheese pizzas were of Deep Dish type, hence the number of D- NC type pizza require to be delivered to Party 1 = 0.25*16 = 4
Consequently, the number of T- NC type pizza require to be delivered to Party 1 = 16 - 4 = 12
We can find out each type of pizza that is required to be delivered to Party 1.
Cost Price of a T-EC pizza = Rs. 500
Cost Price of a D-EC pizza = Rs. 550
Cost Price of a T-NC pizza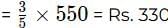 
Cost Price of a D-NC pizza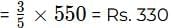 
Therefore the total bill amount for Party 1 = 12*330 + 60*500 + 4*330 + 44*550 = Rs. 59480
Therefore, option (a) is the correct answer.
|
102 videos|123 docs|121 tests
|
FAQs on Practice Question - 65 (Tables) - 100 DILR Questions for CAT Preparation
| 1. What is the significance of tables in data representation? |  |
| 2. How can I prepare for the Tables section of competitive exams? | |
| 3. What common mistakes should I avoid when solving questions related to tables? | |
| 4. Are there specific strategies to quickly analyze tables during exams? | |
| 5. How important is it to understand the context of data presented in tables? | |
Free
,Practice Question - 65 (Tables) | 100 DILR Questions for CAT Preparation
,Sample Paper
,Summary
,ppt
,Extra Questions
,Objective type Questions
,mock tests for examination
,Practice Question - 65 (Tables) | 100 DILR Questions for CAT Preparation
,Viva Questions
,shortcuts and tricks
,past year papers
,study material
,Exam
,MCQs
,practice quizzes
,Semester Notes
,Practice Question - 65 (Tables) | 100 DILR Questions for CAT Preparation
,video lectures
,Important questions
,Previous Year Questions with Solutions
;
Practice Question - 65 (Tables) Free PDF Download
Importance of Practice Question - 65 (Tables)
Practice Question - 65 (Tables) Notes
Practice Question - 65 (Tables) CAT Questions
Study Practice Question - 65 (Tables) on the App
|
© EduRev
|
Education Revolution
|
|
within 7 days!