Quadrilaterals NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Page 94
Q1. Find all the other angles inside the following rectangles.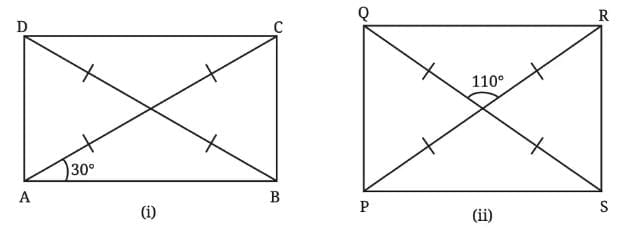
Ans:
(i) 
∠1 + ∠9 = 90° ……… (All corner angles of a rectangle are 90°)
∠1 + 30° = 90°
∠1 = 90° – 30°
∠1 = 60°
∠1 = ∠5 = 60°………. (Alternate interior angles)
∠9 = ∠4 = 30°………. (Alternate interior angles)
In △AOB, OA = OB, then the angles opposite them are equal
∴ ∠9 = ∠7 = 30°
∠7 = ∠3 = 30°………. (Alternate interior angles)
In △AOD, OA = OD, then the angles opposite them are equal
∴ ∠2 = ∠1 = 60°
∠2 = ∠6 = 60°………. (Alternate interior angles)
In △AOB,
∠9 + ∠7 + ∠AOB = 180° ………. (Sum of angles of a triangle)
30° + 30° + ∠AOB = 180°
60° + ∠AOB = 180°
∠AOB = 180° – 60°
∠AOB = 120°
∠AOB = ∠COD = 120° ………… (Vertically opposite angles)
∠AOB + ∠AOD = 180° …………. (Linear pair)
120° + ∠AOD = 180°
∠AOD = 180° – 120°
∠AOD = 60°
∠AOD = ∠BOC = 60° ………… (Vertically opposite angles)
Thus, ∠1 = ∠5 = ∠2 = ∠6 = ∠AOD = ∠BOC = 60°.
∠AOB = ∠COD = 120°.
∠9 = ∠4 = ∠7 = ∠3 = 30°.
(ii)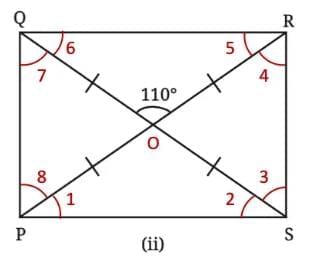 ∠POS = ∠ROQ = 110° ………… (Vertically opposite angles)
∠POS = ∠ROQ = 110° ………… (Vertically opposite angles)
∠POS + ∠POQ = 180° …………. (Linear Pair)
110° + ∠POQ = 180°
∠POQ = 180° – 110°
∠POQ = 70°
∠POQ = ∠SOR = 70° ………… (Vertically opposite angles)
In △POS, OP = OS, then the angles opposite them are equal.
∴ ∠1 = ∠2 = a
In △POS,
∠1 + ∠2 + ∠POS = 180° …………. (Sum of angles of a triangle)
a + a + 110° = 180°
2a = 180° – 110°
2a = 70°
a = 35°
∴ ∠1 = ∠2 = a = 35°
∠1 = ∠5 = 35° ………… (Alternate interior angles)
∠2 = ∠6 = 35° ………… (Alternate interior angles)
Since ABCD is a rectangle, ∠P = 90°
∠9 = ∠1 + ∠8
90° = 35° + ∠8
∠8 = 90° – 35°
∠8 = 55°
∠8 = ∠4 = 55° ………… (Alternate interior angles)
In △POQ, OP = OQ, then the angles opposite them are equal i.e. ∠7 = ∠8 = 55°
∠7 = ∠2 = 55° ………… (Alternate interior angles)
Thus, ∠POS = ∠ROQ = 110°.
∠POQ = ∠SOR = 70°.
∠1 = ∠2 = ∠5 = ∠6 = 35°.
∠8 = ∠4 = ∠7 = ∠2 = 55°
Q2. Draw a quadrilateral whose diagonals have equal lengths of 8 cm that bisect each other, and intersect at an angle of
(i) 30°
(ii) 40°
(iii) 90°
(iv) 140°
Ans:
(i) Draw a line AB equal to 8 cm.
Take point O on AB such that AO = BO = 4 cm.
Using a protractor, draw an angle of 30° at O on OB.
On this line, take points C and D such that OC = OD = 4 cm.
Join AD, DB, BC, and CA.
ABCD is the required quadrilateral.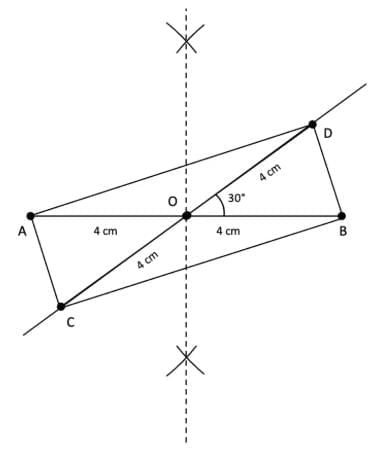
Since diagonals AB and CD are equal and are bisecting each other at O, ACBD is a rectangle.
(ii) Draw a line AB equal to 8 cm.
Take point O on AB such that AO = BO = 4 cm.
Using a protractor, draw an angle of 40° at O on OB.
On this line, take points C and D such that OC = OD = 4 cm.
Join AD, DB, BC, and CA.
ABCD is the required quadrilateral.
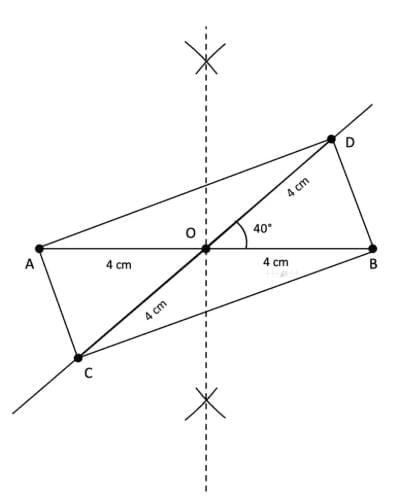
Since diagonals AB and CD are equal and are bisecting each other at O, ACBD is a rectangle.
(iii) Draw a line AB equal to 8 cm.Take a point O on AB such that AO = BO = 4 cm.
Using a protractor, draw an angle of 90° at O on OB.
On this line, take points C and D such that OC = OD = 4 cm.
Join AD, DB, BC, and CA.
ACBD is the required square.
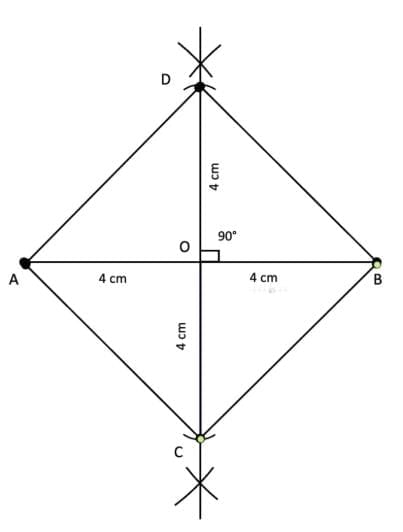
Since diagonals AB and CD are equal and are bisecting each other at M, and also the diagonals are perpendicular to each other, ACBD is a square.
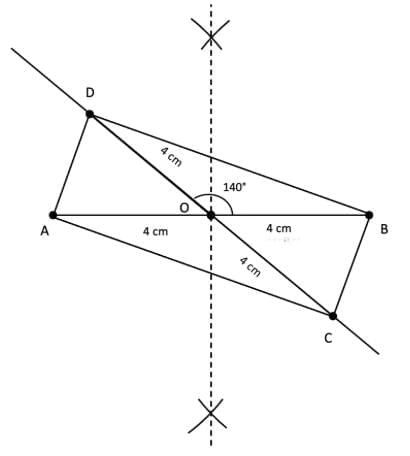
(iv) Draw a line AB equal to 8 cm.Take a point O on AB such that AO = BO = 4 cm.
Using a protractor, draw an angle of 140° at O on OB.
On this line, take points C and D such that OC = OD = 4 cm.
Join AD, DB, BC, and CA.
ACBD is the required quadrilateral.
 Q3. Consider a circle with centre O. Line segments PL and AM are two perpendicular diameters of the circle.
Q3. Consider a circle with centre O. Line segments PL and AM are two perpendicular diameters of the circle.
What is the figure APML? Reason and/or experiment to figure this out.
Ans: 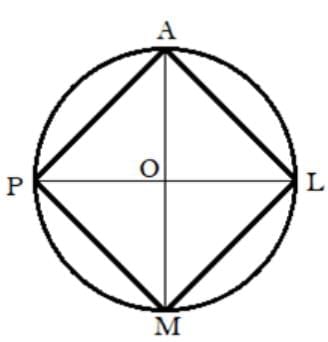 ∴ PL = PO + OL
∴ PL = PO + OL
= r + r
= 2r
and AM = AO + OM
= r + r
= 2r
∴ PL = AM
∴ In the quadrilateral APML, diagonals PL and AM are equal and are perpendicular to each other.
Also, OP = OA = OL = OM = r
∴ Diameters PL and AM bisect each other at O.
∴ Quadrilateral APML is a square.
Q4. We have seen how to get 90° using paper folding. Now, suppose we do not have any paper but two sticks of equal length, and a thread. How do we make an exact 90° using these?
Ans: Let AB and CD be two sticks of equal length, say 6 cm.
Mark the midpoints of the sticks using a ruler.
Fix a screw to the sticks at their midpoints.
Using a thread, measure distances AD and BD.
Keep on moving the sticks about the screw, so that the distances AD and BD are equal.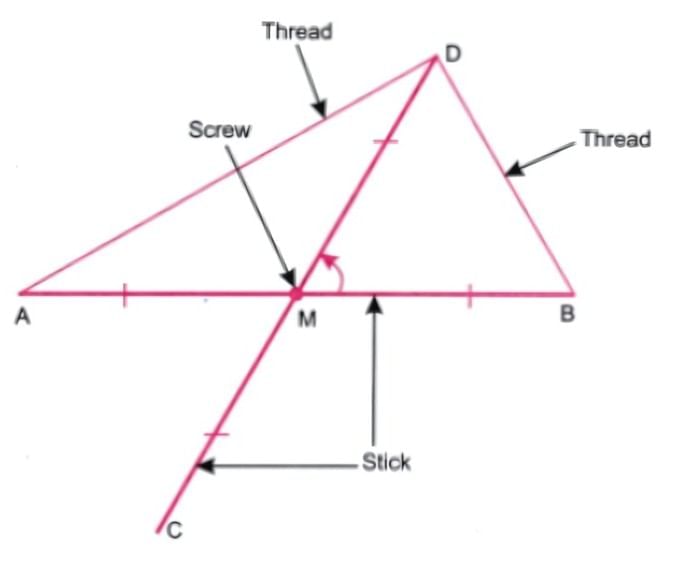
In this position, fix the sticks by tightening the screw.
The new positions of the sticks are shown in the figure.
Tie pieces of thread along AD and BD.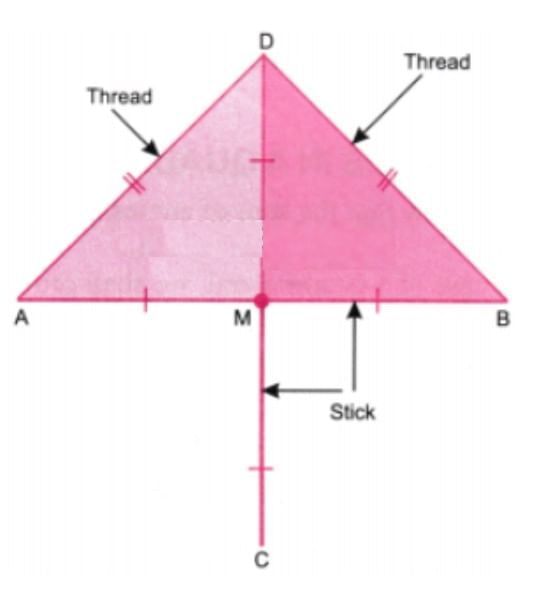
Consider ∆AMD and ∆BMD.
We have AM = BM, AD = BD
and MD is common
∴ By the SSS condition,
∆AMD and ∆BMD are congruent.
∴ ∠AMD = ∠BMD
Also ∠AMD + ∠BMD = 180° (Linear angles)
∴ ∠AMD + ∠AMD = 180°
⇒ 2∠AMD = 180°
⇒ ∠AMD = 90°
∴ ∠AMD = ∠BMD = 90°
∴ Angle between the sticks is 90°.
Q5. We saw that one of the properties of a rectangle is that its opposite sides are parallel. Can this be chosen as a definition of a rectangle? In other words, is every quadrilateral that has opposite sides parallel and equal a rectangle?
Ans: Let ABCD be a quadrilateral in which opposite sides are parallel and equal.
Here AB || DC and AD || BC.
Also, AB = DC and AD = BC.
In the quadrilateral ABCD, opposite sides are equal.
For ABCD to be a rectangle, we require each angle to be 90°.
Given information AB || DC and AD || BC can not help us to prove that each angle of ABCD is 90°.
∴ ABCD may not be a rectangle.
∴ A rectangle can not be defined as a quadrilateral with equal and parallel opposite sides.
Page 102
Figure it Out
Q1. Find the remaining angles in the following quadrilaterals.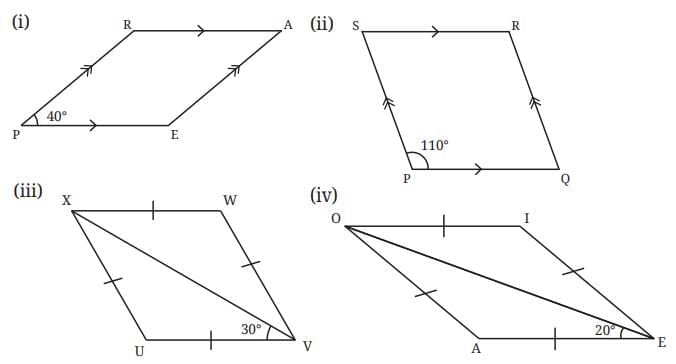
Ans: (i) Here PR ∥ EA, and PE ∥ RA
Therefore, PEAR is a parallelogram.
∠P = ∠A = 40° …………. (Opposite angles of a parallelogram are equal)
∠P + ∠R = 180° …………. (The sum of the adjacent angles of a parallelogram is 180°)
40° + ∠R = 180°
∠R = 180° – 40°
∠R = 140°.
∠R = ∠E = 140° …………. (Opposite angles of a parallelogram are equal)
(ii) Here PQ ∥ SR, and PS ∥ QR
∴ PQRS is a parallelogram.
∠P = ∠R = 110° …………. (Opposite angles of a parallelogram are equal)
∠P + ∠S = 180° …………. (The sum of the adjacent angles of a parallelogram is 180°)
110° + ∠S = 180°
∠S = 180° – 110°
∠S = 70°.
∠S = ∠Q = 70° …………. (Opposite angles of a parallelogram are equal)
(iii) Here, XWUV is a rhombus (all sides equal).
In △VUX, UV = UX, then the angles opposite them are equal.
∴ ∠UXV = ∠UVX = 30°
∠UXV = ∠WXV = 30° …………. (The diagonals of a rhombus bisect its angles)
Also, ∠UVX = ∠WVX = 30° …………. (The diagonals of a rhombus bisect its angles)
∠E = 2 × ∠UVX = 2 × 30° = 60°
∠V = ∠X = 60° …………. (Opposite angles of a rhombus are equal)
∠V + ∠U = 180° …………. (The sum of adjacent angles of a rhombus is 180°)
60° + ∠U = 180°
∠U = 180° – 60°
∠U = 120°
∠U = ∠W = 120° …………. (Opposite angles of a rhombus are equal)
(iv) Here, AEIO is a rhombus (all sides equal).
In △EAO, AE = AO, then the angles opposite them are equal.
∴ ∠AOE = ∠AEO = 20°
∠AEO = ∠IEO = 20° …………. (The diagonals of a rhombus bisect its angles)
Also, ∠AOE = ∠IOE = 20° …………. (The diagonals of a rhombus bisect its angles)
∠E = 2 × ∠AEO = 2 × 20° = 40°
∠E = ∠O = 40° …………. (Opposite angles of a rhombus are equal)
∠E + ∠A = 180° …………. (The sum of adjacent angles of a rhombus is 180°)
40° + ∠A = 180°
∠A = 180° – 40°
∠A = 140°
∠A = ∠I = 140° …………. (Opposite angles of a rhombus are equal)
Q2. Using the diagonal properties, construct a parallelogram whose diagonals are of lengths 7 cm and 5 cm, and intersect at an angle of 140°.
Ans: 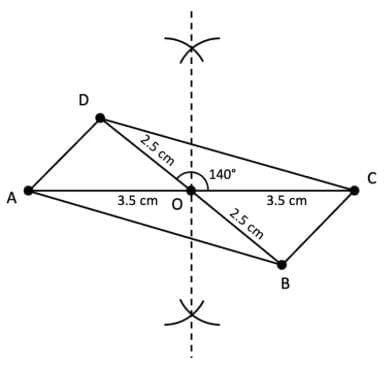
Steps of construction:
(i) Draw a line segment AC of length 7 cm and mark its midpoint as O.
(ii) At point O, draw an angle of 140° with respect to diagonal AC.
(iii) From O, along the 140° line in both directions, mark OD = 2.5 cm OD and OB = 2.5 cm using a compass.
(iv) Join D to A and C.
Join B to A and C.
ABCD is the required parallelogram.
Q3. Using the diagonal properties, construct a rhombus whose diagonals are of lengths 4 cm and 5 cm.
Ans: 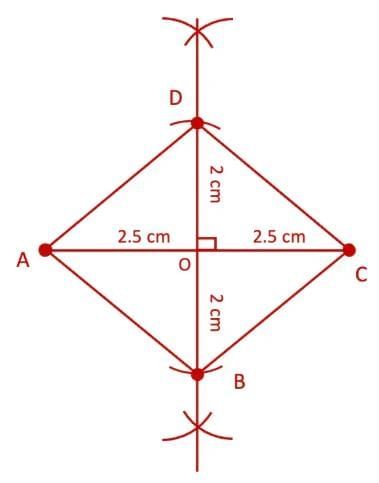
Steps of construction:
(i) Draw a line segment AC of length 5 cm.
(ii) Draw the perpendicular bisector of AC, intersecting it at O.
(iii) With O as centre and radius 2 cm, mark points B (below) and D (above) on the perpendicular bisector.
(iv) Join A–D, D–C, C–B, and B–A.
ABCD is the required rhombus.
Page 107 & 108
Figure it Out
Q1. Find all the sides and the angles of the quadrilateral obtained by joining two equilateral triangles with sides 4 cm.
Ans: 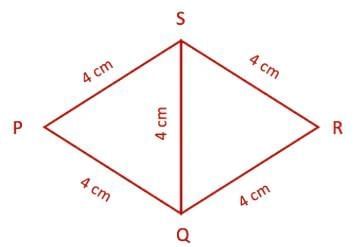
Since all sides of an equilateral triangle are equal.
Thus, the lengths of all sides of the given quadrilateral are equal.
∴ PQ = QR = RS = SP = 4 cm.
Also, the measure of all angles of an equilateral triangle is 60°.
∠P = ∠R = 60°
∠S = ∠PSQ + ∠RSQ = 60° + 60° = 120°.
∠Q = ∠PQR + ∠RQS = 60° + 60° = 120°.
Q2. Construct a kite whose diagonals are of lengths 6 cm and 8 cm.
Ans: 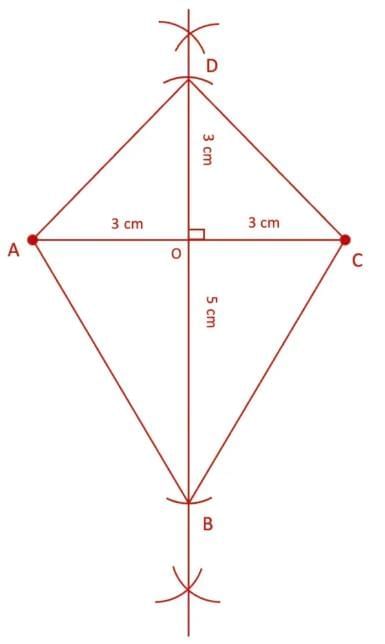
(i) Draw a line segment AC = 6 cm.
(ii) Construct the perpendicular bisector of AC; let it meet AC at O (so O is the midpoint).
(iii) With centre O and radius 3 cm draw an arc to cut the bisector above AC; label that point D. With centre O and radius 5 cm draw an arc to cut the bisector below AC; label that point B.
(iv) Join A − B, B − C, C − D, D − A.
ABCD is the required kite.
Q3. Find the remaining angles in the following trapeziums —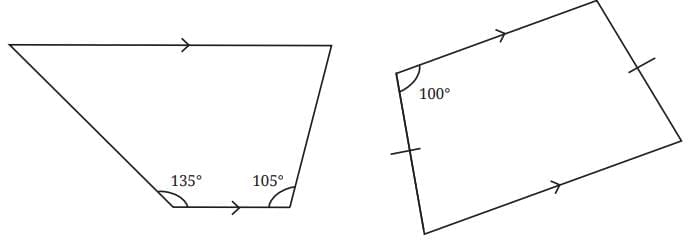 Ans:
Ans: 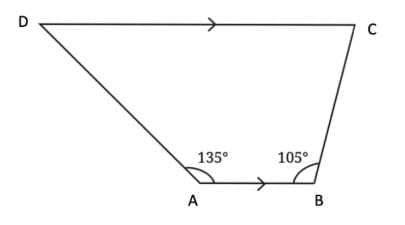 Since AB ∥ DC, and AD is a tranversal, then
Since AB ∥ DC, and AD is a tranversal, then
∠A + ∠D = 180° …………. (Sum of angles on the same side of the transversal)
135° + ∠D = 180°
∠D = 180° – 135°
∠D = 45°
Also, since AB ∥ DC, and BC is a tranversal, then
∠B + ∠C = 180° …………. (Sum of angles on the same side of the transversal)
105° + ∠C = 180°
∠C = 180° – 105°
∠C = 75°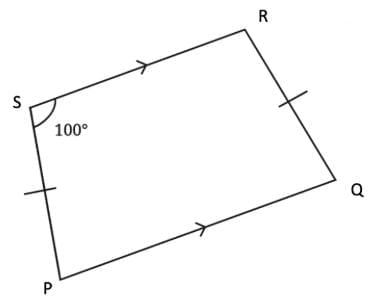
Since PQ ∥ SR, and PS is a tranversal, then
∠P + ∠S = 180° …………. (Sum of angles on the same side of the transversal)
∠P + 100° = 180°
∠P = 180° – 100° = 80°.
∠S = ∠R = 100° …………… (Angles opposite to equal sides are equal)
Also, since PQ ∥ SR, and QR is a tranversal, then
∠Q + ∠R = 180° …………… (Sum of angles on the same side of the transversal)
∠Q + 100° = 180°
∠Q = 180° – 100° = 80°.
Q4. Draw a Venn diagram showing the set of parallelograms, kites, rhombuses, rectangles, and squares. Then, answer the following questions
(i) What is the quadrilateral that is both a kite and a parallelogram?
(ii) Can there be a quadrilateral that is both a kite and a rectangle?
(iii) Is every kite a rhombus? If not, what is the correct relationship between these two types of quadrilaterals?
Ans: (i) The set of rhombuses is common to both the set of kites and the set of parallelograms.
∴ A rhombus is both a kite and a parallelogram.
(ii) A kite is not a rectangle, and a rectangle is not a kite.
∴ There can be no quadrilateral that is both a kite and a rectangle.
Also, there is no common portion of the set of kites and the set of rectangles.
(iii) Every kite is not a rhombus.
In the given figure, the kite ABCD is not a rhombus.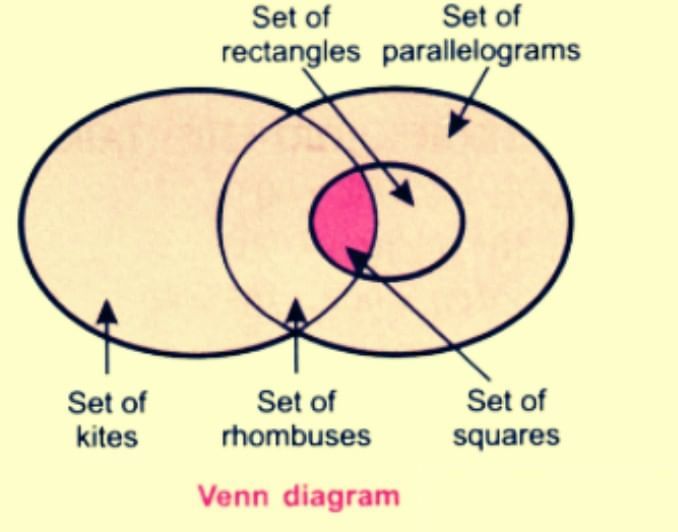
Correct relationship: Every rhombus is a kite, but not every kite is a rhombus.
Q5. If PAIR and RODS are two rectangles, find ∠IOD.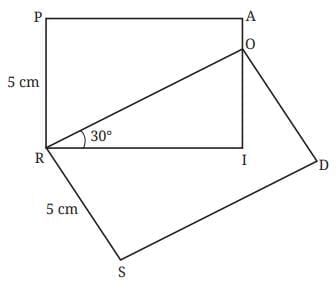 Ans: Since PAIR and RODS are two triangles.
Ans: Since PAIR and RODS are two triangles.
∠RIO = 90° ……… (Corner angle of a rectangle)
In △RIO,
∠IRO + ∠IOR + ∠RIO = 180° …………. (Sum of angles of a triangle)
30° + ∠IOR + 90° = 180°
120° + ∠IOR = 180°
∠IOR = 180° – 120° = 60°.
∴ ∠IOD = 90° – ∠IOR = 90° – 60° = 30°.
Q6. Construct a square with a diagonal 6 cm without using a protractor.
Ans: 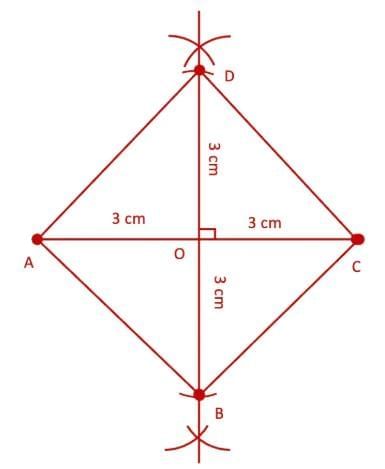
Steps of construction:
(i) Draw a line segment AC = 6 cm and mark its midpoint as O.
(ii) With O as centre and radius greater than half of AC, draw arcs above and below AC from points A and C.
(iii) Join the arc intersections to get a line perpendicular to AC and passing through O.
(iv) Again, with O as centre and radius equal to 3 cm, mark points B and D on the perpendicular line.
(v) Connect A–B–C–D–A.
Hence, ABCD is the required square with a diagonal of 6 cm.
Q7. CASE is a square. The points U, V, W and X are the midpoints of the sides of the square. What type of quadrilateral is UVWX? Find this by using geometric reasoning, as well as by construction and measurement. Find other ways of constructing a square within a square such that the vertices of the inner square lie on the sides of the outer square, as shown in Figure (b).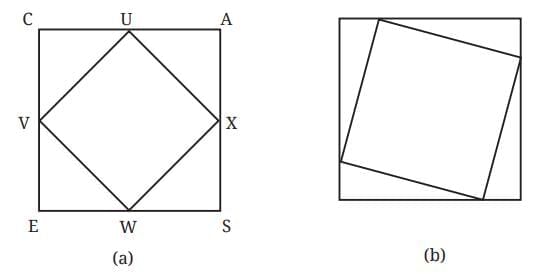
Ans: (a) U, V, W, and X are the midpoints of the sides of the square.
In ∆VCU and ∆UAX,
we have VC = UA, ∠VCU = ∠UAX = 90°, and CU = AX.
∴ By the SAS condition, ∆VCU and ∆UAX are congruent.
∴ VU = UX
Similarly, VU = XW, VU = WV.
∴ Sides of the quadrilateral UVWX are equal.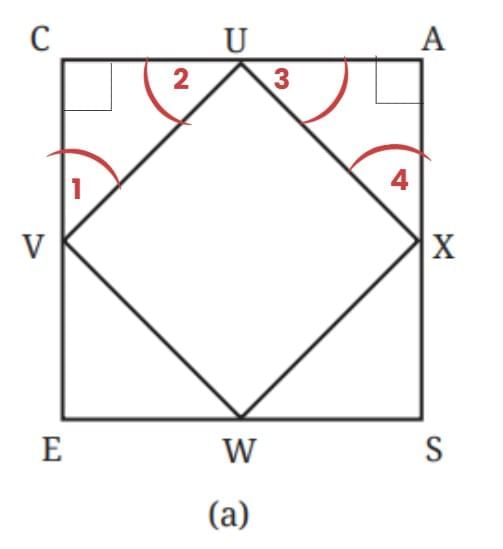
In ∆VCU, VC = CU
⇒∠1 = ∠2
Also, ∠1 + ∠C + ∠2 = 180°
⇒∠1 + 90° + ∠1 = 180°
⇒2∠1 = 90°
⇒∠1 = 45°
∴ ∠2 is also 45°.
Similarly, ∠3 = ∠4 = 45°
We have ∠2 + ∠VUX + ∠3 = 180°
⇒45° + ∠VUX + 45° = 180°
⇒∠VUX = 180° – 90°
⇒ ∠VUX = 90°
Similarly, ∠VXW = 90°, ∠XWV = 90° and ∠WVU = 90°.
∴ By definition, the quadrilateral UVWX is a square.
(b) Let ABCD be a square.
Take points P, Q, R, and S such that AS = BP = CQ = DR.
Since the sides of squares are equal,
we have DS = AP = BQ = CR.
In ∆PAS and ∆SDR, we have
PA = SD, ∠PAS = ∠SDR = 90°, and AS = DR.
∴ By the SAS condition, ∆PAS and ∆SDR are congruent.
∴ PS = SR
Similarly, PS = RQ, PS = QP.
∴ Sides of the quadrilateral PQRS are equal.
In ∆PAS, ∠1 + ∠2 + 90° = 180°
⇒∠1 + ∠2 = 90°
⇒∠3 + ∠2 = 90° (∵ ∠1 = ∠3)
Also, ∠2 + ∠4 + ∠3 = 180°
⇒ 90° + ∠4 = 180°
⇒ ∠4 = 180° – 90°
⇒ ∠4 = 90°
∴ Similarly, ∠5 = 90°, ∠6 = 90°, and ∠7 = 90°.
By definition, the quadrilateral PQRS is a square.
Q8. If a quadrilateral has four equal sides and one angle of 90°, will it be a square? Find the answer using geometric reasoning as well as by construction and measurement.
Ans: Reasoning:
- A rhombus is a quadrilateral with four equal sides.
- If a rhombus has one angle of 90°, then:
- Its opposite angle is also 90° (opposite angles of a rhombus are equal).
- Each adjacent angle must also be 90° (sum of adjacent angles in a parallelogram/rhombus is 180°).
- Thus, all four angles are 90°.
- Since the quadrilateral has all sides equal and all angles right angles, it is a square.
Construction and measurement: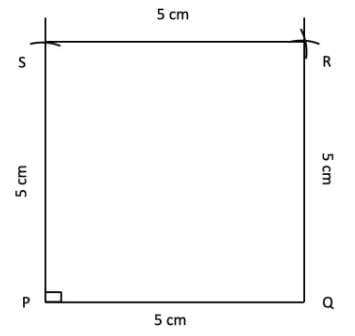
Steps of construction:
(i) Draw a line segment PQ of length 5 cm.
(ii) At point PP, construct a perpendicular line to PQ.
(iii) On this perpendicular, mark point S such that PS = 5 cm.
(iv) With S as centre and radius 5 cm, draw an arc to the right of PS.
(v) With Q as centre and radius 5 cm, draw an arc above PQ to intersect the arc from step (4) at point R.
Join Q–R, R–S, and S–P to complete the square PQRS.
Verification by measurement:
All sides: PQ = QR = RS = SP = 5 cm
All angles: ∠P =∠Q =∠R =∠S = 90°.
Conclusion: The figure constructed is a square.
Q9. What type of quadrilateral is one in which the opposite sides are equal? Justify your answer.
Hint: Draw a diagonal and check for congruent triangles.
Ans: If a quadrilateral has opposite sides equal, then it is a parallelogram.
Geometric reasoning using a diagonal: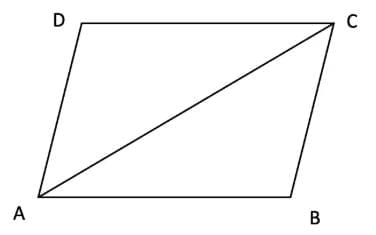
Given: Quadrilateral ABCD with AB = CD and BC = DA.
Draw diagonal AC.
In △ABC and △CDA,
AB = CD (given)
BC = DA (given)
AC = AC (common side)
By SSS congruence, △ABC ≅ △CDA.
From congruence, corresponding angles are equal:
∠BAC =∠DCA and ∠ACB =∠CAD.
But these are alternate interior angles.
∴ AB ∥ DC and AD ∥ BC.
Hence, ABCD is a parallelogram.
Q10. Will the sum of the angles in a quadrilateral such as the following one also be 360°? Find the answer using geometric reasoning as well as by constructing this figure and measuring.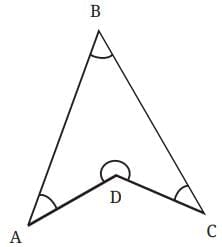 Ans: Yes, the sum of the angles in a quadrilateral will always be 360°.
Ans: Yes, the sum of the angles in a quadrilateral will always be 360°.
Construction: Mark four non-collinear points as A, B, C, and D, and join them to form a quadrilateral ABCD.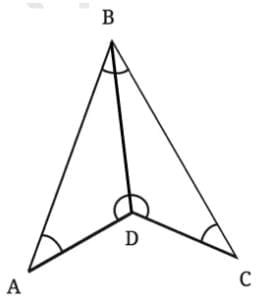
Geometric reasoning:
In quad. ABCD, join BD to divide it into two triangles.
Now, In △BAD,
∠DBA + ∠BAD + ∠ADB = 180° ……….(1)……. (Sum of angles of a triangle)
In △BCD,
∠BCD + ∠CDB + ∠DBC = 180° ……….(2)……. (Sum of angles of a triangle)
Adding (1) and (2), we get
∠DBA + ∠BAD + ∠ADB + ∠BCD + ∠CDB + ∠DBC = 180° + 180°
(∠DBA + ∠DBC) + (∠ADB + ∠CDB) + ∠BAD + ∠BCD = 360°
∠ABC + ∠ADC + ∠BAD + ∠BCD = 360°
Thus, the sum of the angles of the given quadrilateral is 360°.
Q11. State whether the following statements are true or false. Justify your answers.
(i) A quadrilateral whose diagonals are equal and bisect each other must be a square.
Ans: False.
A quadrilateral whose diagonals are equal and bisect each other is a rectangle. A square is a special case of a rectangle where all sides are also equal.
(ii) A quadrilateral having three right angles must be a rectangle.
Ans: True.
Let ABCD be a quadrilateral having three right angles at A, D, and C.
We have ∠A + ∠B + ∠C + ∠D = 360°.
⇒ 90° + ∠B + 90° + 90° = 360°
⇒ ∠B = 360° – 270°
⇒ ∠B = 90°.
∴ Each angle of ABCD is 90°.
∴ Given quadrilateral is a rectangle.
(iii) A quadrilateral whose diagonals bisect each other must be a parallelogram.
Ans: True.
If the diagonals bisect each other, then the two triangles formed by a diagonal are congruent, which gives pairs of opposite sides parallel. Hence the figure is a parallelogram.
(iv) A quadrilateral whose diagonals are perpendicular to each other must be a rhombus.
Ans: False.
Squares, kites, and some other quadrilaterals also have perpendicular diagonals. Therefore, having perpendicular diagonals does not necessarily mean the quadrilateral is a rhombus.
(v) A quadrilateral in which the opposite angles are equal must be a parallelogram.
Ans: True.
Let ABCD be a quadrilateral in which ∠1 = ∠3 and ∠2 = ∠4.
We have, ∠1 + ∠2 + ∠3 + ∠4 = 360°.
⇒ ∠1 + ∠2 + ∠1 + ∠2 = 360°
⇒ 2(∠1 + ∠2) = 360°
⇒ ∠1 + ∠2 = 180°
AB is a transversal of lines AD and BC, and the sum of internal angles ∠1 and ∠2 on the same side is 180°.
∴ Lines AD and BC are parallel.
Again, ∠1 + ∠2 + ∠3 + ∠4 = 360°
⇒ ∠3 + ∠2 + ∠3 + ∠2 = 360°
⇒ 2(∠2 + ∠3) = 360°
⇒ ∠2 + ∠3 = 180°
BC is a transversal of lines AB and DC, and the sum of internal angles ∠2 and ∠3 on the same sides is 180°.
∴ Lines AB and DC are parallel.
∴ Opposite sides of quadrilateral ABCD are parallel.
∴ ABCD is a parallelogram.
∴ The given statement is true
(vi) A quadrilateral in which all the angles are equal is a rectangle.
Ans: True
If all four angles are equal, each angle must be 360°/4 = 90°. A quadrilateral with four right angles is a rectangle.
(vii) Isosceles trapeziums are parallelograms.
Ans: False.
An isosceles trapezium has exactly one pair of parallel sides and the non-parallel sides equal while a parallelogram must have two pairs of parallel sides. So an isosceles trapezium is not a parallelogram.
|
26 videos|133 docs|11 tests
|
FAQs on Quadrilaterals NCERT Solutions - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the properties of quadrilaterals in geometry? |  |
| 2. How can we calculate the area of different types of quadrilaterals? |  |
| 3. What is the significance of diagonals in quadrilaterals? |  |
| 4. Can you explain the difference between convex and concave quadrilaterals? |  |
| 5. How do we prove that a quadrilateral is a parallelogram? |  |

















