Number Play NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Page 122
Figure it Out
Q1. The sum of four consecutive numbers is 34. What are these numbers?
Ans: Let four consecutive numbers be x, (x + 1), (x + 2) and (x + 3).
x + (x + 1) + (x + 2) + (x + 3) = 34
x + x + 1 + x + 2 + x + 3 = 34
4x + 6 = 34
4x = 34 – 6
4x = 28
x = 28/7 = 7.
So, (x + 1 ) = 7 + 1 = 8
(x + 2) = 7 + 2 = 9
(x + 3) = 7 + 3 = 10
Therefore, the given four consecutive numbers are 7, 8, 9, and 10.
Q2. Suppose p is the greatest of five consecutive numbers. Describe the other four numbers in terms of p.
Ans: Given p is the greatest of five consecutive numbers.
The other four numbers in terms of p are (p – 1), (p – 2), (p – 3), and (p – 4).
p – 1 is the second largest number
p – 2 is the third largest number
p – 3 is the second smallest number
p – 4 is the smallest number
∴ p > (p – 1) > (p – 2) > (p – 3) > (p – 4).
Q3. For each statement below, determine whether it is always true, sometimes true, or never true. Explain your answer. Mention examples and non-examples as appropriate. Justify your claim using algebra.
(i) The sum of two even numbers is a multiple of 3.
Ans: Let the two even numbers be 2a + 2b
Sum = 2a + 2b = 2(a + b)
For 2(a + b) to be a multiple of 3, (a + b) must be multiple of 3.
Example:
2 + 4 = 6 → divisible by 3
2 + 8 = 10 → not divisible by 3
Conclusion: Sometimes true.
(ii) If a number is not divisible by 18, then it is also not divisible by 9.
Ans: If a number is divisible by 18, then it is also divisible by 9 because 9 is a factor of 18.
18a ÷ 9 = 2a → divisible by 9.
But if a number is divisible by 9, it is not always divisible by 18.
9b ÷ 18 = b/2 → not divisible by 9.
Example: 9 is divisible by 9 but not divisible by 18.
27 is divisible by 9 but not 18.
Conclusion: Sometimes true.
(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
Ans: Let the two numbers be a and b.
Not divisible by 6 means they do not satisfy 6∣a or 6∣b.
But their sum can still be divisible by 6.
Example: 2 and 4 → both not divisible by 6.
But, 2 + 4 = 6 → divisible by 6.
Conclusion: Sometimes true.
(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
Ans: Let the multiple of 6 be 6a, the multiple of 9 be 9b.
Sum: 6a + 9b = 3(2a + 3b)→ clearly divisible by 3.
Example:
6 + 9 = 15 → divisible by 3.
12 + 18 = 30 → divisible by 3.
Conclusion: Always true.
(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
Ans: Let multiple of 6 be 6a, multiple of 3 be 3b.
Sum: 6a + 3b = 3(2a + b).
For it to be divisible by 9, 2a + b must be divisible by 3.
Example:
6 (6 × 1) + 3 (3 × 1) = 9 →divisible by 9
6 + 6 = 12 → not divisible by 9
Conclusion: Sometimes true.
Q4. Find a few numbers that leave a remainder of 2 when divided by 3 and a remainder of 2 when divided by 4. Write an algebraic expression to describe all such numbers.
Ans: Here, Remainder = 2, Dividend = 3
∴ Number = (Quotient × Dividend) + Remainder = (K × 3) + 2
where, K = 1, 2, 3,…..
Numbers = 1 × 3 + 2 = 3 + 2 = 5
Numbers = 2 × 3 + 2 = 6 + 2 = 8
Numbers = 3 × 3 + 2 = 9 + 2 = 11
Thus, 5, 8, and 11 are numbers that leave a remainder of 2 when divided by 3.
Algebraic expression = 3K + 2
Here, Remainder = 2, dividend = 4
Number = 4K + 2, where K = 1, 2, 3, 4, …
Numbers = 4 × 1 + 2 = 4 + 2 = 6
Numbers = 4 × 2 + 2 = 8 + 2 = 10
Numbers = 4 × 3 + 2 = 12 + 2 = 14
Algebraic expression = 4K + 2
Thus, 6, 10, and 14 are numbers that leave a remainder of 2 when divided by 4.
Q5. “I hold some pebbles, not too many, When I group them in 3’s, one stays with me. Try pairing them up — it simply won’t do, A stubborn odd pebble remains in my view. Group them by 5, yet one’s still around, But grouping by seven, perfection is found. More than one hundred would be far too bold, Can you tell me the number of pebbles I hold?”
Ans: Grouped in 3’s leaves 1.
Pairing (2’s) leaves 1.
Grouped by 5 leaves 1.
Grouped by 7 is perfect.
Number ≤ 100.
L.C.M of 2, 3, and 5 = 30.
In all those cases, when we group them, 1 pebble remains.
So, the actual number of pebbles must be = 30 + 1 = 31, but 31 is not divisible by 7.
The next multiple of 30 is 2 × 30 = 60.
So, 60 + 1 = 61, but this is also not divisible by 7.
Similarly, the next number is 90 + 1 = 91.
And 91 is divisible by 7.
Hence, the number of pebbles I hold = 91.
Q6. Tathagat has written several numbers that leave a remainder of 2 when divided by 6. He claims, “If you add any three such numbers, the sum will always be a multiple of 6.” Is Tathagat’s claim true?
Ans: A number that leaves remainder of 2 when divided by 6 can be written as 6k + 2.
Three such numbers are: (6a + 2), (6b + 2), (6c + 2).
(6a + 2) + (6b + 2) + (6c + 2) = 6(a + b + c) + 6 = 6(a + b + c + 1).
This sum is divisible by 6.
So yes, Tathagat’s claim is always true.
Example: Take 20, 26, 32 → sum = 78 → divisible by 6.
Take 2, 8, 14 → sum = 24 → divisible by 6.
Page 123
Q7. When divided by 7, the number 661 leaves a remainder of 3, and 4779 leaves a remainder of 5. Without calculating, can you say what remainders the following expressions will leave when divided by 7? Show the solution both algebraically and visually.
(i) 4779 + 661
(ii) 4779 – 661
Ans: Given, 661 = K × 7 + 3, where K = 1, 2, 3, 4, …
and, 4779 = K × 7 + 5
Algebraic Method:
(i) 4779 + 661
4779 = (682 × 7 ) + 5
Remainder = 5
661 = (94 × 7) + 3
Remainder = 3
∴ 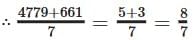 = 1 = Remainder
= 1 = Remainder
(ii) 4779 – 661
∴ 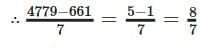 = 4 = Remainder
= 4 = Remainder
Visualization Method:
(i) 4779 + 661 = (682 × 7) + 5 + (94 × 7) + 3
= 7 × (682 + 94) + 5 + 3
= 7 × 776 + 8
= Divisible by 7 + 8/7
= 1, Remainder
(ii) 4779 – 661 = (682 × 7) + 5 – (94 × 7) – 3
= 7 × (682 – 94) + 5 – 3
= 7 × 588 + 2
= Divisible by 7 + 2
= 2, Remainder
Q8. Find a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5. What is the smallest such number? Can you give a simple explanation of why it is the smallest?
Ans: A number that leaves a remainder of 2 when divided by 3 is = 3x + 2
A number that leaves a remainder of 3 when divided by 4 is = 4x + 3
A number that leaves a remainder of 4 when divided by 5 is = 5x + 4
L.C.M of 3, 4, and 5 = 60
All the numbers are the same, so 4x + 3 = 3x + 2
4x – 3x = 2 – 3
x = -1
Each remainder is 1 less than the divisor.
Hence, the number is 1 less than the L.C.M = (60 – 1) = 59.
So, 59 is the smallest number that satisfies all the given conditions.
Page 126
Figure it Out
Q1. Find, without dividing, whether the following numbers are divisible by 9.
(i) 123
Ans: Digit sum of the number 123 = (1 + 2 + 3) = 6
Now, (6 ÷ 9) is not divisible by 9.
So, the whole number 123 is not divisible by 9.
(ii) 405
Ans: Digit sum of the number 405 = (4 + 0 + 5) = 9
Now, (9 ÷ 9) = 1,divisible by 9.
So, the whole number 405 is divisible by 9.
(iii) 8888
Ans: Digit sum of the number 8888 = (8 + 8 + 8 + 8) = 32
Now, (32 ÷ 9) is not divisible by 9.
So, the whole number 8888 is not divisible by 9.
(iv) 93547
Ans: Digit sum of the number 93547 = (9 + 3 + 5 + 4 + 7) = 9
Now, (28 ÷ 9) is not divisible by 9.
So, the whole number 93547 is not divisible by 9.
(v) 358095
Ans: Digit sum of the number 358095 = (3 + 5 + 8 + 0 + 9 + 5) = 30
Now, (30 ÷ 9) is not divisible by 9.
So, the whole number 358095 is not divisible by 9.
Q2. Find the smallest multiple of 9 with no odd digits.
Ans: If we multiply 9 by odd digits, we will get odd digits as a result.
So, we will multiply 9 by only even digits.
- 18 ( 1 is odd)
- 36 ( 3 is odd)
- 72 (7 is odd)
- 90 (9 is odd)
- 108 ( 1 is odd)
- 216 ( 1 is odd)
- 288(2 + 8 + 8 = 18 → divisible by 9, and digits 2,8,8 are even)
Q3. Find the multiple of 9 that is closest to the number 6000.
Ans: First Divide 6000 by 9 → (6000 ÷ 9) →Quotient = 666 and Remainder = 6
So, 5994 is 6 less than 6000.
And next closest number is 667×9 = 6003, 6003 is 3 greater than 6000.
Hence, the closest to the number 6000 that is multiple of 9 = 6003.
Q4. How many multiples of 9 are there between the numbers 4300 and 4400?
Ans: The multiples of 9 are there between the numbers 4300 and 4400 are 4302, 4311, 4320,………, 4392
The number of multiples of 9 =  =
= 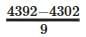 +1
+1
= 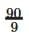 + 1= 10 + 1
+ 1= 10 + 1
= 11
Thus, the multiples of 9 are 11.
Page 130
Q: Between the numbers 600 and 700, which numbers have the digital root:
(i) 5
(ii) 7
(iii) 3
Ans:
(i) Digital root 5:
608 = 6 + 0 + 8 = 14 = 1 + 4 = 5;
617 = 6 + 1 + 7 = 14 = 1 + 4 = 5;
662 = 6 + 6 + 2 = 14 = 1 + 4 = 5;
689 = 6 + 8 + 9 = 23 = 2 + 3 = 5, etc.
(ii) Digital root 7:
610 = 6 + 1 + 0 = 7;
619 = 6 + 1 + 9 = 16 = 1 + 6 = 7;
637 = 6 + 3 + 7 = 16 = 1 + 6 = 7;
673 = 6 + 7 + 3 = 16 = 1 + 6 = 7, etc.
(iii) Digital root 3:
606 = 6 + 0 + 6 = 12 = 1 + 2 = 3;
615 = 6 + 1 + 5 = 12 = 1 + 2 = 3;
633 = 6 + 3 + 3 = 12 = 1 + 2 = 3;
678 = 6 + 7 + 8 = 21 = 2 + 1 = 3, etc.
Q: Write the digital roots of any 12 consecutive numbers. What do you observe?
Ans: The digital roots of any 12 consecutive numbers are:
- 105 = 1 + 0 + 5 = 6;
- 106 = 1 + 0 + 6 = 7;
- 107 = 1 + 0 + 7 = 8;
- 108 = 1 + 0 + 8 = 9;
- 109 = 1 + 0 + 9 = 10 = 1 + 0 = 1;
- 110 = 1 + 1 + 0 = 2;
- 111 = 1 + 1 + 1 = 3;
- 112 = 1 + 1 + 2 = 4;
- 113 = 1 + 1 + 3 = 5;
- 114 = 1 + 1 + 4 = 6;
- 115 = 1 + 1 + 5 = 7;
- 116 = 1 + 1 + 6 = 8
Observation:
The digital roots of cycles repeat after 9 numbers.
6 → 7 → 8 → 9 → 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8
So, the digital roots of consecutive numbers form a repeating cycle of length 9.
The digital root of multiples by 9:
- 405 = 4 + 0 + 5 = 9;
- 234 = 2 + 3 + 4 = 9;
- 1035 = 1 + 0 + 3 + 5 = 9;
- 936 = 9 + 3 + 6 = 18 = 1 + 8 = 9, etc.
Q: We saw that the digital root of multiples by 9 is always 9. Now, find the digital roots of some consecutive multiples of (i) 3, (ii) 4, and (iii) 6.
Ans:
(i) The digital roots of some consecutive multiples of 3 are:
39 = 3 + 9 = 12 = 1 + 2 = 3;
42 = 4 + 2 = 6;
45 = 4 + 5 = 9;
48 = 4 + 8 = 12 = 1 + 2 = 3;
51 = 5 + 1 = 6;
54 = 5 + 4 = 9;
57 = 5 + 7 = 12 = 1 + 2 = 3;
60 = 6 + 0 = 6;
63 = 6 + 3 = 9 etc.
Thus, the digital roots of consecutive multiples of 3 are 3, 6, 9, 3, 6, 9,……
(ii) The digital roots of some consecutive multiples of 4 are:
32 = 3 + 2 = 5;
36 = 3 + 6 = 9;
40 = 4 + 0 = 4;
44 = 4 + 4 = 8;
48 = 4 + 8 = 12 = 1 + 2 = 3;
52 = 5 + 2 = 7;
56 = 5 + 6 = 11 = 1 + 1 = 2;
60 = 6 + 0 = 6, etc.
Thus, the digital roots of consecutive multiples of 4 are 5, 9, 4, 8, 3, 7, 2, 6,……..
(iii) The digital roots of some consecutive multiples of 6 are:
30 = 3 + 0 = 3;
36 = 3 + 6 = 9;
42 = 4 + 2 = 6;
48 = 4 + 8 = 12 = 1 + 2 = 3;
54 = 5 + 4 = 9;
60 = 6 + 0 = 6;
66 = 6 + 6 = 12 = 1 + 2 = 3;
72 = 7 + 2 = 9;
78 = 7 + 8 = 15 = 1 + 5 = 6, etc.
Thus, the digital roots of consecutive multiples of 6 are 3, 9, 6, 3, 9, 6, 3, 9, 6,……….
Q: What are the digital roots of numbers that are 1 more than a multiple of 6? What do you notice? Try to explain the patterns noticed.
Ans: The digital roots of the numbers that are 1 more than a multiple of 6 are:
37 = 3 + 7 = 10 = 1 + 0 = 1;
43 = 4 + 3 = 7;
49 = 4 + 9 = 13 = 1 + 3 = 4;
55 = 5 + 5 = 10 = 1 + 0 = 1;
61 = 6 + 1 = 7;
67 = 6 + 7 = 13 = 1 + 3 = 4, etc.
Hence, the digital roots of the numbers that are 1 more than a multiple of 6 are 1, 7, 4, 1, 7, 4,…..
We notice the digital roots cycle through 1, 7, 4, and then repeat: 1, 7, 4, 1, 7, 4, 1, 7, 4,………
Q: I’m made of digits, each tiniest and odd, No shared ground with root #1 – how odd!
My digits count, their sum, my root – All point to one bold number’s pursuit – The largest odd single-digit I proudly claim. What’s my number? What’s my name?
Ans: Try: 111 111 111
Digits = 9
Sum = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 9
Digital root = 9
All digits are odd (1)
Satisfies all the conditions.
Hence, the answer is 111 111 111.
Page 131
Figure it Out
Q1. The digital root of an 8-digit number is 5. What will be the digital root of 10 more than that number?
Ans: Consider the 8-digit number 80000006.
The digital root of 80000006 = 8 + 0 + 0 + 0 + 0 + 0 + 0 + 6
= 14
= 1 + 4
= 5
10 more than 80000006 = 80000006 + 10 = 80000016
The digital root of 80000016 = 8 + 0 + 0 + 0 + 0 + 0 + 1 + 6
= 15
= 1 + 5
= 6
Thus, the digital root of 10 more than 80000006 is 6.
Q2. Write any number. Generate a sequence of numbers by repeatedly adding 11. What would be the digital roots of this sequence of numbers? Share your observations.
Ans: Consider the number = 40
The sequence of numbers by repeatedly adding 11 are 40, 51(40 + 11), 62(51 + 11), 73(62 + 11), 84(73 + 11), 95(84 + 11), 106(95 + 11), 117(106 + 11), 128(117 + 11), 139(128 + 11), etc.
The digital roots of this sequence of numbers are:
40 = 4 + 0 = 4;
51 = 5 + 1 = 6;
62 = 6 + 2 = 8;
73 = 7 + 3 = 10 = 1 + 0 = 1;
84 = 8 + 4 = 12 = 1 + 2 = 3;
95 = 9 + 5 = 14 = 1 + 4 = 5;
106 = 1 + 0 + 6 = 7;
117 = 1 + 1 + 7 = 9;
128 = 1 + 2 + 8 = 11 = 1 + 1 = 2;
139 = 1 + 3 + 9 = 13 = 1 + 3 = 4,… etc.
Thus, the digital roots of this sequence of numbers are 4, 6, 8, 1, 3, 5, 7, 9, 2, 4,…..
Observations:
The digital roots are 4, 6, 8, 1, 3, 5, 7, 9, 2, 4,……
This sequence starts repeating after 9 steps.
So the digital roots form a cycle: 4, 6, 8, 1, 3, 5, 7, 9, 2, 4,……
Q3. What will be the digital root of the number 9a + 36b + 13?
Ans: First Method:
The digital root of the number 9a + 36b + 13 = 9a + 36b + 9 + 4
= 9(a + 4b + 1) + 4
= 9 + 4
= 13 [∵ The digital root of multiples of 9 is always 9.]
= 1 + 3
= 4
Thus, the digital root of the number 9a + 36b + 13 will be 4.
Second Method:
We have 9a + 36b + 13
Here, a and b are integers
Put a = 1, b = 1,
9a + 36b + 13 = 9 × 1 + 36 × 1 + 13
= 9 + 36 + 13
= 58
The digital root of 58 = 5 + 8 = 13 = 1 + 3 = 4
Put a = 2, 6 = 3,
9a + 36b + 13 = 9 × 2 + 36 × 3 + 13
= 18 + 108 + 13
= 139
The digital root of 139 = 1 + 3 + 9 = 13 = 1 + 3 = 4
Thus, the expression 9a + 36b + 13 always has a digital root of 4.
Q4. Make conjectures by examining if there are any patterns or relations between
(i) the parity of a number and its digital root.
(ii) the digital root of a number and the remainder obtained when the number is divided by 3 or 9.
Ans: Consider the pattern: 8, 16, 24, 32, 40,……
(i) 8 = 8 = digital root, parity → even
16 = 1 + 6 = 7 = digital root, parity → odd
24 = 2 + 4 = 6 = digital root, parity → even
32 = 3 + 2 = 5 = digital root, parity → odd
40 = 4 + 0 = 4 = digital root, parity → even
(ii) Divided by 3
8 ÷ 3 ⇒ 2, Remainder
24 ÷ 3 ⇒ 0, Remainder
32 ÷ 3 ⇒ 2, Remainder
40 ÷ 3 ⇒ 1, Remainder
Divided by 9
8 ÷ 9 ⇒ 8, Remainder
24 ÷ 9 ⇒ 6, Remainder
32 ÷ 9 ⇒ 5, Remainder
40 ÷ 9 ⇒ 4, Remainder
Page 132-134
Figure it Out
Q1. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? Explain why there are two answers to this problem.
Ans: We know that the digital root of multiples of 9 is always 9.
So, the digit root of the number 31z5 is = 9
Hence the value of z = 0 or 9.
Proceedings:
Therefore, 3 + 1 + z + 5 = 9
Or, 9 + z = 9
Or, z = 0
Now, the expression 3 + 1 + z + 5 = 9 + z must be divisible by 9.
If z = 0, then 9 + z = 9 is divisible by 9.
And when z = 9, then 9 + z = 18 is divisible by 9.
So, the value of z = 0 or 9.
And the numbers are 3105 and 3195.
That’s why there are two answers to this problem.
Q2. “I take a number that leaves a remainder of 8 when divided by 12. I take another number which is 4 short of a multiple of 12. Their sum will always be a multiple of 8”, claims Snehal. Examine his claim and justify your conclusion.
Ans: 1st number = 12k + 8
2nd number = 12k - 4
Sum = 12k + 8 + 12k - 4 = 24k + 4
According to Snehal, it is always a multiple of 8.
If we put k = 1, 24 × 1 + 4 = 24, which is a multiple of 8.
k = 2, 24 × 2 + 4 = 48, which is a multiple of 8.
k = 3, 24 × 3 + 4 = 76, which is not a multiple of 8.
So, her claim is “Sometimes True”.
Q3. When is the sum of two multiples of 3, a multiple of 6 and when is it not? Explain the different possible cases, and generalise the pattern.
Ans: Multiples of 3 are: 3, 6, 9, 12, 15, 18,……….
3 + 6 = 9, not a multiple of 6.
6 + 9 = 15, not a multiple of 6.
3 + 9 = 12, multiple of 6.
6 + 12 = 18, multiple of 6.
There are two possible cases.
- If both numbers are odd, then the sum is a multiple of 6.
- If both numbers are even, then the sum is a multiple of 6.
Q4. Sreelatha says, "I have a number that is divisible by 9. If I reverse its digits, it will still be divisible by 9 ".
(i) Examine if her conjecture is true for any multiple of 9.
(ii) Are any other digit shuffles possible such that the number formed is still a multiple of 9?
Ans: Consider a number that is divisible by 9 = 72
We know that,
If the sum of the digits is divisible by 9, then the number is divisible by 9.
If its digits are reversed
27 = 2 + 7 = 9, it is also divisible by 9.
(i) True
(ii) Yes, any other digit shuffle is possible that the number is still a multiple of 9.
Q5. If 48a23b is a multiple of 18, list all possible pairs of values for a and b.
Ans: 48a23b is a multiple of 18.
As we know that,
If the number is a multiple of 18, then it is also a multiple of 2 and 9.
∴ 48a23b
Sum of the digits = 4 + 8 + a + 2 + 3 + b = 17 + a + b
Case 1: Put a = 1 and b = 0
481230, it is possible values of a and b.
Sum = 18, it is divisible by 9.
Case 2: Put a = 4 and b = 6
484236
Sum = 17 + 10 = 27, it is divisible by 9.
Thus, the possible values of a and 6 are a = 1 and b = 0, a = 4 and b = 6; there are two possible cases.
Q6. If 3p7q8 is divisible by 44, list all possible pairs of values for p and q.
Ans: Given by question, 3p7q8 is divisible by 44.
As we know, if a number is divisible by 44, then it is also divisible by 4 and 11.
∴ 3p7q8
Case 1: Put p = 1 and q = 0
37708 is divisible by 4 and 11, then it is also divisible by 44.
Case 2: Put p = 5 and q = 2
35728 is divisible by 4 and 11, then it is also divisible by 44.
Case 3: Put p = 3 and q = 4
33748 is divisible by 4 and 11, then it is also divisible by 44.
Case 4: Put p = 1 and q = 6
31768 is divisible by 4 and 11, then it is also divisible by 11.
Thus, (p = 7, q = 0), (p = 5, q = 2), (p = 3, q = 4), and (p = 1 and q = 6) are the possible pairs of values for p and q.
Q7. Find three consecutive numbers such that the first number is a multiple of 2, the second number is a multiple of 3, and the third number is a multiple of 4. Are there more such numbers? How often do they occur?
Ans: Let x, x + 1 and (x + 2) be the three numbers
Put x = 2, ⇒ 2, 3, 4
Put x = 14, ⇒ 14, 15, 6
Put x = 26, ⇒ 26, 27, 28
Put x = 38, ⇒ 38, 39, 40
Thus, the three consecutive numbers are (14, 15, 16),
Put x = 26, ⇒ 26, 27, 28
(26, 27, 28) and (38, 39, 40)
There are infinite numbers, spaced apart by 12.
Q8. Write five multiples of 36 between 45,000 and 47,000. Share your approach with the class.
Ans: Step:
We know that if a number is a multiple of 36, then it is also a multiple of 4 and 9.
45000
Last two digits = 00, it is divisible by 4.
Sum of the digits = 4 + 5 + 0 + 0 + 0 = 9, it is also divisible by 9.
Thus, 45000 is completely divisible by 36.
The five multiples of 36 between 45,000 and 47,000.
(45,000 + 36), (45,000 + 2 × 36), (45,000 + 3 × 36), (45,000 + 4 × 36) and (45,000 + 5 × 36)
i.e., 45,036, 45,072, 45,108, 45,144, and 45,180.
Q9. The middle number in the sequence of 5 consecutive even numbers is 5p. Express the other four numbers in sequence in terms of p.
Ans: Let be the 5 consecutive even numbers are = x, (x + 2), (x + 4), (x + 6), (x + 8)
The middle number is (x + 4)
Therefore, (x + 4) = 5p
Or, x = 5p – 4
So, the other four numbers are =
1st number → 5p – 4
2nd number → 5p – 2
4th number → 5p + 2
5th number → 5p + 4
Q10. Write a 6-digit number that it is divisible by 15, such that when the digits are reversed, it is divisible by 6.
Ans: We know that if the number is divisible by 3 and 5, then it is also divisible by 15.
Consider the number 643215.
Sum of the digits = 6 + 4 + 3 + 2 + 1 + 5 = 21, which is divisible by 3.
Thus, 643215 is divisible by 3.
One’s place = 5, it is also divisible by 5.
Hence, 643215 is divisible by 15.
One’s place is not 0, because the digits are reversed, it becomes a 5-digit number.
Lakhs place is always taken as an even number.
Reversed the digits:
512346
One’s place = 6, 512346 is divisible by 2.
Sum of the digits = 5 + 1 + 2 + 3 + 4 + 6 = 21.
It is also divisible by 3.
Hence, 512346 is divisible by 6.
Q11. Deepak claims, “There are some multiples of 11 which, when doubled, are still multiples of 11. But other multiples of 11 don’t remain multiples of 11 when doubled”. Examine if his conjecture is true; explain your conclusion.
Ans: The multiples of 11 are: 11, 22, 33, 44, 55,…
When doubled, 22, 44, 66, 88, 110,……
i.e. (11) × 2, 11 × 4, 11 × 6, 11 × 8, 11 × 10,…. are also multiples of 11.
False, if multiples of 11 are doubled, then the multiples of 11 are these numbers.
Q12. Determine whether the statements below are ‘Always True’, ‘Sometimes True’, or ‘Never True’. Explain your reasoning.
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
Ans: ‘Always True’
Explanation: Let be the two numbers are = 6a and 3b.
So the product of these = (6a × 3b) = 18ab
It saws that 18ab is also divisible by 9. [18 is a multiple of 9]
Example: If a = 3 and b = 2
(18 × 3 × 2) = 108, so 108 is a multipleof p.
(ii) The sum of three consecutive even numbers will be divisible by 6.
Ans: ‘Always True’
Explanation: Let be the first consecutive even number = x
So the other consecutive even numbers = (x + 2) and (2 + 4)
Therefore, sum of these number = x + x + 2 + x + 4 = 3x + 6 = 3(x + 2)
Example: If x = 6, then 3(6 + 2) = 24, divisible by 6.
When x = 10, then 3(10 + 2) = 36, divisible by 6.
(iii) If abcdef is a multiple of 6, then badcef will be a multiple of 6.
Ans: ‘Always True’
Explanation: If a number is divisible by 6 it must be divisible by 2 and 3.
Checking divisibility by 2: We check the last digits of the number, if it is even then the number must be divisible by 2.
And checking divisibility by 3: We check the sum of the digits of the number if it is divisible by 3, then the number is also divisible by 3.
Here we can see that the last digit of both the numbers ‘abcdef’ and ‘badcef’ is the same and all the digits are the same, only their positions have changed.
So, if abcdef is a multiple of 6, then badcef should be a multiple of 6.
(iv) 8 (7b-3)-4 (11b+1) is a multiple of 12.
Ans: ‘Never True’
Explanation: 8 × (7b - 3) – 4 × (11b + 1)
= 56b –24 – 44b – 4
= 12b – 28
We see that 12b is a multiple of 12 but 28 is not a multiple of 12.
So, we say that 12b – 28 is not divisible by 12.
Q13. Choose any 3 numbers. When is their sum divisible by 3? Explore all possible cases and generalise.
Ans: Let the three numbers be n1, n2, and n3.
Let their remainders when divided by 3 be r1, r2, and r3.
The sum n1 + n2 + n3 is divisible by 3 if and only if r1 + r2 + r3 is divisible by 3.
Case 1: All remainders are 0.
r1 = 0, r2 = 0, r3 = 0
Sum of remainders = 0 + 0 + 0 = 0, which is divisible by 3.
Case 2: All remainders are 1.
r1 = 1, r2 = 1, r3 = 1
Sum of remainders = 1 + 1 + 1 = 3, which is divisible by 3.
Case 3: All remainders are 2.
r1 = 2, r2 = 2, r3 = 2
Sum of remainders = 2 + 2 + 2 = 6, which is divisible by 3.
Case 4: One remainder is 0, one is 1, and one is 2.
r1 = 0, r2 = 1, r3 = 2 (in any order).
Sum of remainders = 0 + 1 + 2 = 3, which is divisible by 3.
The sum of three numbers is divisible by 3 if and only if all three numbers have the same remainder when divided by 3, or if they all have different remainders when divided by 3.
Q14. Is the product of two consecutive integers always multiple of 2? Why? What about the product of these consecutive integers? Is it always a multiple of 6? Why or why not? What can you say about the product of 4 consecutive integers? What about the product of five consecutive integers?
Ans: Yes, the product of two consecutive integers is always a multiple of 2.
1 × 2 = 2, 2 × 3 = 6, 5 × 6 = 30, 10 × 11 = 110, and so on.
Since we know that multiplying by an odd number and an even number is always an even number.
No, it is not always a multiple of 6.
1 × 2 = 2, 4 × 5 = 20, 7 × 8 = 56
Since it is not divisible by 6.
The product of 4 consecutive integers
2 × 3 × 4 × 5 = 120,
4 × 5 × 6 × 7 = 840,
5 × 6 × 7 × 8 = 1680
We can say that the product of 4 consecutive integers, divisible by 12.
The product of five consecutive integers is:
1 × 2 × 3 × 4 × 5 = 120,
2 × 3 × 4 × 5 × 6 = 720,
3 × 4 × 5 × 6 × 7 = 2520
Hence, we can say that the product of five consecutive integers is always divisible by 24.
Q15. Solve the cryptarithms —
(i) EF × E = GGG
(ii) WOW × 5 = MEOW
Ans: (i) EF × E = GGG
=10E + F × E = 100 G + 10G + G
= (10E + F) × E = 111G
If E = 1, then 10 + F = 111G
[It is not possible because for any value of F, LHS can't be equal to RHS]
If E = 2, then (20 + F) × 2 = 111G
[It is also not possible because for any value of F, LHS can't be equal to RHS]
For E = 3, then (30 + F) × 3 = 111G
=90 + 3F = 111G
If F = 7 and G = 1, then LHS = RHS.
∴ The values of E, F, and G are 3, 7, and 1, respectively.
(ii) WOW × 5 = MEOW
Using the same process as the previous one.
(100W + 10O + W) × 5 = MEOW
⇒ (101 W + 10 O) × 5 = MEOW
⇒ 505 W + 50 O = MEOW
Let’s try possible values of W and O such that the result is a 4-digit number.
If we set W = 5 and O = 7, we obtain a 4-digit number.
505 × 5 + 50 × 7 = 2875
On the right-hand side, if MEOW = 2875
W = 5, O = 7
1000M + 100E + 10O + W = 1000M + 100E + 70 + 5 = 1000M + 100E + 75
If we take M = 2 and E = 8, then it satisfies the LHS.
So, the values of M, E, O, and W are 2, 8, 7, and 5, respectively.
Q16. Which of the following Venn diagrams captures the relationship between the multiples of 4, 8, and 32?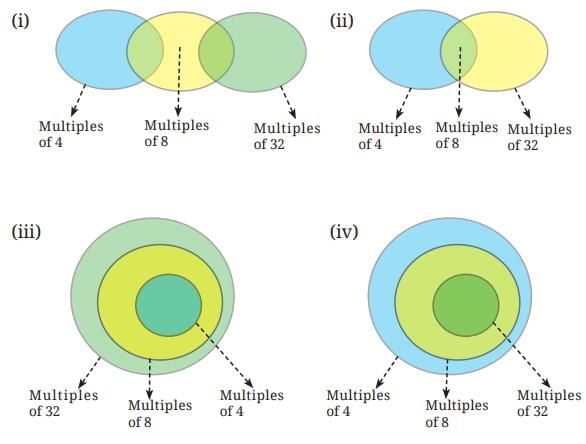 Ans: The correct answer is option (iv).
Ans: The correct answer is option (iv).
(iv) Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64,…
Multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64,….
Multiples of 32 are: 32, 64, 96, 128,…
The Venn diagram captures the relationship between the multiples of 4, 8, and 32: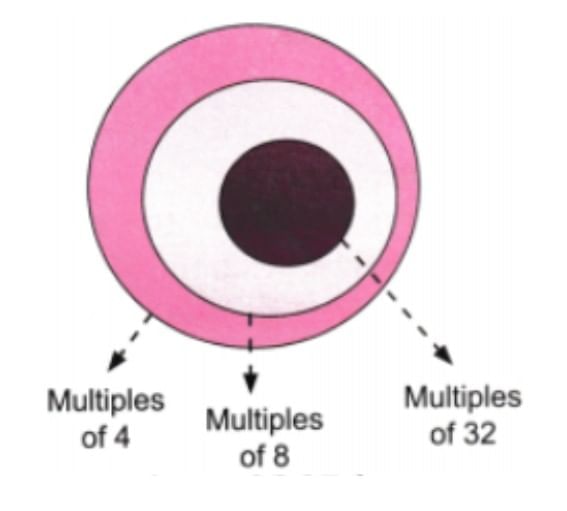
|
26 videos|133 docs|11 tests
|
FAQs on Number Play NCERT Solutions - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the importance of learning number play in Class 8 mathematics? |  |
| 2. How can students effectively practice number play concepts to improve their skills? |  |
| 3. What are some common number patterns and sequences that students should be familiar with? |  |
| 4. How does number play relate to real-life situations and problem-solving? |  |
| 5. What strategies can teachers use to make number play engaging for students? |  |
















