We Distribute, Yet Things Multiply NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Page 142
Q1. Observe the multiplication grid below. Each number inside the grid is formed by multiplying two numbers. If the middle number of a 3 × 3 frame is given by the expression pq, as shown in the figure, write the expressions for the other numbers in the grid.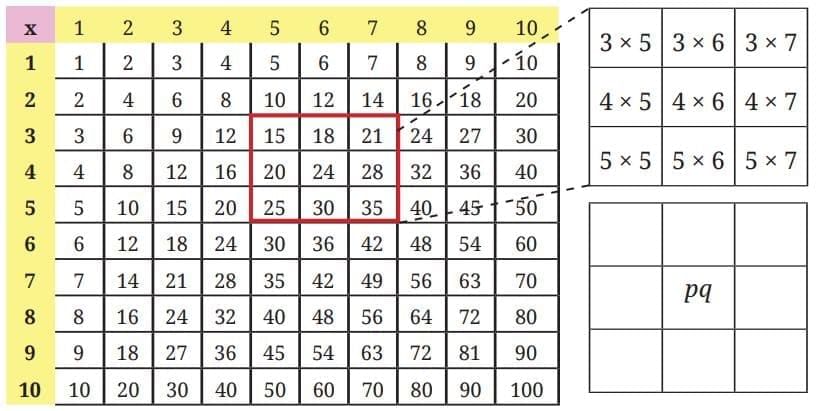
Ans: 
Q2. Expand the following products.
(i) (3 + u) (v – 3)
(ii) 2/3 (15 + 6a)
(iii) (10a + b) (10c + d)
(iv) (3 – x) (x – 6)
(v) (–5a + b) (c + d)
(vi) (5 + z) (y + 9)
Ans: (i) (3 + u) (v – 3)
We have, (3 + u) (v – 3)
= 3(v – 3) + u(v – 3)
= 3v – 9 + uv – 3u
= 3v – 3u + uv – 9
(ii) 2/3 (15 + 6a)
2/3 × 15 + 2/3 × 6a
= 2 × 5 + 2 × 2a
= 10 + 4a.
(iii) (10a + b) (10c + d)
= (10a + b)10c + (10 a + b)d
= 100ac + 10bc + 10ad + bd.
(iv) (3 – x) (x – 6)
= (3 – x)x – (3 – x)6
= 3x – x2 – (18 – 6x)
= 3x – x2 – 18 + 6x
= – x2 + 6x + 3x – 18
= – x2 + 9x – 18.
(v) (–5a + b) (c + d)
= (–5a + b)c + (–5a + b)d
= – 5ac + bc – 5ad + bd
= – 5ac – 5ad + bc + bd.
(vi) (5 + z) (y + 9)
= (5 + z)y + (5 + z)9
= 5y + zy + 45 + 9z
= 5y + 9z + zy + 45.
Q3. Find 3 examples where the product of two numbers remains unchanged when one of them is increased by 2 and the other is decreased by 4.
Ans: If the two numbers are x and y, then:
x × y = (x + 2) × (y − 4)
xy = (x + 2)y – (x + 2)4
xy = xy + 2y – (4x + 8)
xy = xy + 2y – 4x – 8
xy – xy = 2y – 4x – 8
0 = 2y – 4x – 8
4x + 8 = 2y
2(2x + 4) = 2y
y = 2x + 4.
Examples:
(i) x = 1, y = 6 → Product = 1 × 6 = 6
Check: (1 + 2) × (6 − 4) = 3 × 2 = 6.
(ii) x = 2, y = 8→ Product = 16
Check: (2 + 2) × (8 − 4) = 4 × 4 =16.
(iii) x = 5, y =14 → Product = 5 × 14 = 70
Check: (5 + 2) × (14 − 4) = 7 × 10 = 70.
Therefore, (1, 6), (2, 8), and (5, 14) are three valid examples.
Q4. Expand (i) (a + ab – 3b2) (4 + b), and (ii) (4y + 7) (y + 11z – 3).
Ans: (i) (a + ab – 3b2) (4 + b)
= (a + ab – 3b2)4 + (a + ab – 3b2)b
= 4a + 4ab – 12b2 + ab + ab2 – 3b3
= – 3b3 – 12b2 + ab2 + 4ab + ab + 4a
= – 3b3 – 12b2 + ab2 + 5ab + 4a.
(ii) (4y + 7) (y + 11z – 3)
= (4y + 7)y + (4y + 7)11z – (4y + 7)3
= 4y2 + 7y + 44yz + 77z – (12y + 21)
= 4y2 + 7y + 44yz + 77z – 12y – 21
= 4y2 + 7y – 12y + 44yz + 77z – 21
= 4y2 – 5y + 44yz + 77z – 21.
Q5. Expand (i) (a – b) (a + b), (ii) (a – b) (a2 + ab + b2) and (iii) (a – b)(a3 + a2b + ab2 + b3), Do you see a pattern? What would be the next identity in the pattern that you see? Can you check it by expanding?
Ans: (i) (a − b)(a + b)
= (a − b)a + (a − b)b
= a2 – ab + ab – b2
= a2 – b2.
(ii) (a – b) (a2 + ab + b2)
= (a – b)a2 + (a – b)ab + (a – b)b2
= a3 – a2b + a2b – ab2 + ab2 – b3
= a3 – b3.
(iii) (a – b)(a3 + a2b + ab2 + b3)
= (a – b)a3 + (a – b)a2b + (a – b)ab2 + (a – b)b3
= a4 – a3b + a3b – a2b2 + a2b2 – ab3 + ab3 – b4
= a4 – b4.
We observe the following pattern (a – b) (an + an-1 b + ….. + bn) = an+1 – bn+1
The next identity would be: (a − b)(a4 + a3b + a2b2 + ab3 + b4) = a5 − b5.
Page 149
Figure it Out
Q1. Which is greater: (a – b)2 or (b – a)2? Justify your answer.
Ans: Here, (a – b)2 = a2 + b2 – 2ab ……….(1)
and (b – a)2 = b2 + a2 – 2ba
b2 + a2 = a2 + b2 and ba = ab
(b – a)2 = a2 + b2 – 2ab ……….(2)
Comparing (1) and (2), we get (a – b)2 = (b – a)2
Q2. Express 100 as the difference of two squares.
Ans: Therefore, a2 – b2 = 100
Or, a2 – b2 = 2 × 2 × 5 × 5
Or, (a + b) (a – b) = 50 × 2
When, (a + b) = 50 and (a – b) = 2
Then ‘a’ should be = 26 and ‘b’ should be = 24
So, (a + b) (a – b) = (26 + 24) (26 – 24) = 262 – 242 = 676 – 576 = 100
Therefore, 100 = 262 – 242
Q3. Find 4062, 722, 1452, 10972, and 1242 using the identities you have learnt so far.
Ans:
4062
= (400+6)2
= (400)2 + (6)2 + 2×400×6
= 160000 + 36 + 4800
= 164836
722
= (70 + 2)2
= (70)2 + (2)2 + 2×70×2
= 4900 + 4 + 280
= 5184
1452
= (150- 5)2
= (150)2 + (5)2 – 2×150×5
= 22500 + 25 – 1500
= 21025
10972
= (1100- 3)2
= (1100)2 + (3)2 – 2×1100×3
= 1210000 + 9 – 6600
= 1203409
1242
= (100+ 24)2
= (100)2 + (24)2 + 2×100×24
= 10000 + 576 + 4800
= 15376
Q: Do Patterns 1 and 2 hold only for counting numbers? Do they hold for negative integers as well? What about fractions? Justify your answer.
Ans: Pattern 1
2(a2 + b2) = (a + b)2 + (a – b)2
Case-I
Let a = 4, b = 2
LHS = 2(42 + 22) = 2 × (16 + 4) = 40
RHS = (4 + 2)2 + (4 – 2)2 = 36 + 4 = 40
∴ Pattern 1 holds for counting numbers.
Case-II
Let a = -4, b = -2
LHS = 2((-4)2 + (-2)2)
= 2 × (16 + 4)
= 2 × 20
= 40
RHS = (-4 + (-2))2 + (-4 – (-2))2
= (-4 – 2)2 + (-4 + 2)2
= (-6)2 + (-2)2
= 36 + 4
= 40
LHS = RHS
∴ Pattern 1 holds for negative integers also.
Case-III
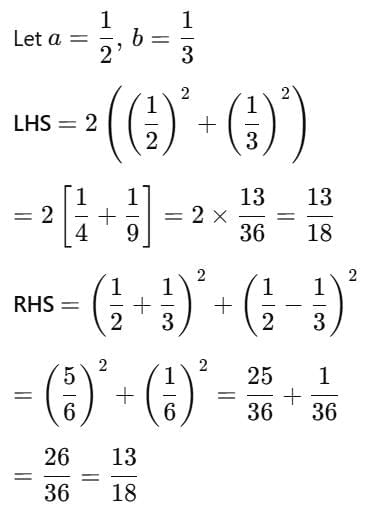
The pattern holds for fractions also.
Pattern 2
a2 – b2 = (a + b) (a – b)
Case-I
Let a = 5, b = 3
LHS = 52 – 32 = 25 – 9 = 16
RHS = (5 + 3) (5 – 3) = 8 × 2 = 16
∴ LHS = RHS
∴ Pattern 2 holds for counting numbers.
Case-II
Let a = -5, b = -3
Now, LHS = (-5)2 – (-3)2 = 25 – 9 = 16
and RHS = [(-5) + (-3)] [(-5) – (-3)]
= (-5 – 3) (-5 + 3)
= (-8) (-2)
= 16
∴ LHS = RHS
∴ Pattern 2 holds for negative integers also.
Case III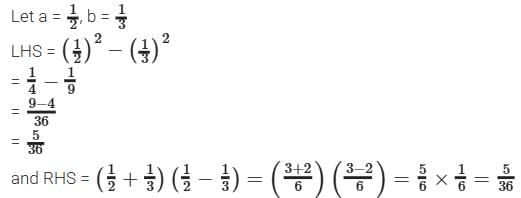
∴ LHS = RHS
∴ Pattern 2 holds for fractions also.
Page 154 - 155
Figure it Out
Q1. Compute these products using the suggested identity.
(i) 462using Identity 1A for (a + b)2
Ans: Identity (a + b)2 = a2 + 2ab + b2
So, 462 = (40 + 6)2
= (40)2 + 2 × 40 × 6 + (6)2
= 1600 + 480 + 36
= 2116
(ii) 397 × 403 using Identity 1C for (a + b) (a – b)
Ans: Identity (a + b) (a – b) = a2 – b2
So, 397 × 403
= (400 – 3) × (400 + 3)
= (400)2 – (3)2
= 160000 – 9
= 159991
(iii) 912 using Identity 1B for (a – b)2
Ans: Identity (a – b)2 = a2 + b2 – 2ab
So, 912 = (100 – 9)2
= (100)2 + (9)2 – 2×100×9
= 10000 + 81 –1800
= 8281
(iv) 43 × 45 using Identity 1C for (a + b) (a – b)
Ans: Identity (a + b) (a – b) = a2 – b2
So, 43 × 45
= (44 – 1) (44 + 1)
= (44)2 – (1)2
= 1936 – 1
= 1935
Q2. Use either a suitable identity or the distributive property to find each of the following products.
(i) (p – 1)(p + 11)
Ans: Distributive property
∴ (p – 1) (p + 11) = p2 + 11p – p – 11 = p2 + 10p – 11
(ii) (3a – 9b)(3a + 9b)
Ans: Identity (a + b) (a – b)
∴ (3a – 9b) (3a + 9b) = (3a)2 – (9b)2 = 9a2 – 81b2
(iii) – (2y + 5) (3y + 4)
Ans: Distributive property
∴ – (2y + 5) (3y + 4) =-6y2 – 8y – 15y – 20 = -6y2 – 23y – 20
(iv) (6x + 5y)2
Ans: Identity(a + b)2
∴ (6x + 5y)2 = (6x)2 + 2 × 6x × 5y + (5y)2 = 36x2 + 60xy + 25y2
(v) (2x – 1/2)2
Ans: Identity (a – b)2
∴ (2x – 1/2)2 = (2x)2 + (1/2)2 – 2 × 2x × 1/2 = 4x2 + 1/4 – 2x
(vi) (7p) × (3r) × (p + 2)
Ans: Distributive property
∴ (7p) × (3r) × (p + 2) = 21pr × (p + 2) = 21p2r + 42pr
Q3. For each statement identify the appropriate algebraic expression(s).
(i) Two more than a square number.
2 + s, (s + 2)2, s2 + 2, s2 + 4, 2s2, 22s
Ans: s2 + 2
Explanation: Let be the number = s
∴ Square number = s2
So, two more the square number is = s2+ 2
(ii) The sum of the squares of two consecutive numbers
m²+n2, (m + n)2, m2 + 1, m2 + (m + 1)2, m2 + (m – 1)2, {m + (m + 1)}2, (2m)2 + (2m + 1)2
Ans: m2 + (m + 1)2
Explanation: Let be the consecutive numbers are = m and (m + 1)
So, the sum of the square numbers = m2 + (m + 1)2
Q4. Consider any 2 by 2 square of numbers in a calendar, as shown in the figure.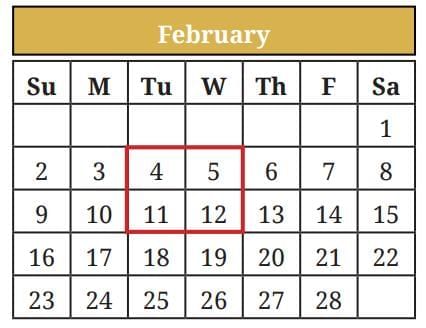
Find products of numbers lying along each diagonal — 4 × 12 = 48, 5 × 11 = 55. Do this for the other 2 by 2 squares. What do you observe about the diagonal products? Explain why this happens.
Hint: Label the numbers in each 2 by 2 square as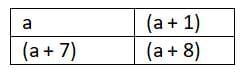
Ans: Case - I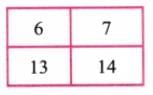
Here, 6 × 14 = 84
13 × 7 = 91
Difference = 91 – 84 = 7
Case-II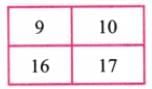
Here, 9 × 17 = 153
16 × 10 = 160
Difference = 160 – 153 = 7
We observe that the difference of the diagonal products in both cases is always 7.
Q5. Verify which of the following statements are true.
(i) (k + 1)(k + 2) – (k + 3) is always 2.
Ans: Statement is false.
Explanation: (k + 1) (k + 2) – (k + 3)
= k2 + 2k + k + 2 – k – 3
= k2 + 2k – 1
Now, if k = 1, then (1)2 + 2 × 1 – 1 = 2
If k = 2, then (2)2 + 2 × 2 – 1 = 7
If k = 3, then (3)2 + 2 × 3 – 1 = 14
(ii) (2q + 1)(2q – 3) is a multiple of 4.
Ans: Statement is false.
Explanation: (2q + 1) (2q – 3)
= 4q2 – 6q + 2q – 3
= 4q2 – 4q – 3
=4(q2 –q) – 3
Here we see that 3 is not divisible by 4, so the entire equation is not divisible by 4.
(iii) Squares of even numbers are multiples of 4, and squares of odd numbers are 1 more than multiples of 8.
Ans: Statement is true.
Explanation: Let be the even number is = 2n (even is always divisible by 2).
∴ Square of 2n = (2n)2 = 4n2 (We see it is always a multiple of 4)
And the odd number is = 2n + 1
∴ Square of 2n + 1 = (2n + 1)2 = (2n)2 + 2×2n×1 + 12 = 4n2 + 4n + 1 = 4(n2 + n) + 1
(n2 + n) is always an even number because n is odd, the square of an odd number is always odd, and odd + odd = even.
Example: If (n2 + n) = 2, then 4×2 + 1 = 9 (9 is 1 more than multiples of 8)
If (n2 + n) = 4, then 4×4 + 1 = 17 (9 is 1 more than multiples of 8) etc.
(iv) (6n + 2)2 – (4n + 3)2 is 5 less than a square number.
Ans: Statement is false.
Explanation: (6n + 2)2 – (4n + 3)2
= {(6n)2 + 2×6n×2 + (2)2} –{(4n)2 + 2×4n×3 + (3)2}
= 36n2 + 24n + 4 – 16n2 – 24n – 9
= 20n2– 5
Clearly we see 20 is a square number so 20n2 is also not a square number.
Q6. A number leaves a remainder of 3 when divided by 7, and another number leaves a remainder of 5 when divided by 7. What is the remainder when their sum, difference, and product are divided by 7?
Ans: Let the numbers be x and y.
x = 7a + 3, y = 7b + 5
Sum = x + y
= 7a + 3 + 7b + 5
= 7(a + b) + 8
= 7(a + b) + 7 + 1
= 7(a + b + 1) + 1
∴ The remainder on division by 7 is 1.
Difference = x – y
= (7a + 3) – (7b + 5)
= 7a + 3 – 7b – 5
= 7(a – b) – 2
= 7(a – b) – 1 + 5 (∵ -2 = -7 + 5)
= 7(a – b – 1) + 5
∴ The remainder on division by 7 is 5.
Product = xy
= (7a + 3) (7b + 5)
= 49ab + 35a + 21b + 15
= (49ab + 35a + 21b + 14) + 1
= 7(7ab + 5a + 3b + 2) + 1
∴ The remainder on division by 7 is 1.
Q7. Choose three consecutive numbers, square the middle one, and subtract the product of the other two. Repeat the same with other sets of numbers. What pattern do you notice? How do we write this as an algebraic equation? Expand both sides of the equation to check that it is a true identity.
Ans: Let be the three consecutive numbers are = x, (x + 1), (x + 2)
Therefore,(x + 1)2 – x(x + 2)
= x2 + 2x + 1 – x2 – 2x
= 1
And let be the other sets of consecutive numbers are = (x – 1), x, (x + 1)
Therefore, x2 – (x – 1) (x + 1)
= x2 – x2 – x + x + 1
= 1
In the pattern we have observed, the value of the equation is always 1.
Hence, the algebraic equation is:-(x + 1)2 – x(x + 2) = 1
Q8. What is the algebraic expression describing the following steps-add any two numbers. Multiply this by half of the sum of the two numbers? Prove that this result will be half of the square of the sum of the two numbers.
Ans: Let be the two numbers are = x and y
Sum of these numbers are = (x + y)
Multiplying this by half = 1/2 × (x + y)
Now, 1/2 × (x + y) × (x + y)
= (x + y)2/2
Therefore, the result will be half of the square of the sum of the two numbers.
Q9. Which is larger? Find out without fully computing the product.
(i) 14 × 26 or 16 × 24
(ii) 25 × 75 or 26 × 74
Ans:
(i) Let p = 14 × 26
p’ = 16 × 24
= (14 + 2) (26 – 2)
= 14 × 26 + 2 × 26 – 14 × 2 – 2 × 2
= 14 × 26 + 2(26 – 14 – 2)
= 14 × 26 + 2 × 10
p’ = p + 2 × 10
∴ p’ > p or 16 × 24 > 14 × 26
(ii) Let p = 25 × 75
p’ = 26 × 74
= (25 + 1) (75 – 1)
= 25 × 75 + 75 × 1 – 25 × 1 – 1 × 1
= p + (75 – 25 – 1)
= p + 49
∴ p’ > p or 26 × 74 > 25 × 75
Q10. A tiny park is coming up in Dhauli. The plan is shown in the figure. The two square plots, each of area g2 sq. ft., will have a green cover. All the remaining area is a walking path w ft. wide that needs to be tiled. Write an expression for the area that needs to be tiled.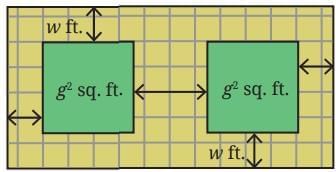
Ans: Area of square plot = g2 sq. ft., so length of side = g ft.
∴ Length of the tiny park = (w + g + w + g + w) ft= (3w + 2g) ft
And breadth of the tiny park = (w + g + w) = (2w + g) ft
Total area of the park = (3w + 2g) × (2w + g)
= 6w2 + 3wg + 4wg + 2g2
= (6w2 + 7wg + 2g2) sq. ft.
So, the remaining area that needs to be tiled for the walking path is
= (6w2 + 7wg + 2g2) – (g2) sq. ft.
= (6w2 + 7wg + g2) sq. ft.
Q11. For each pattern shown below,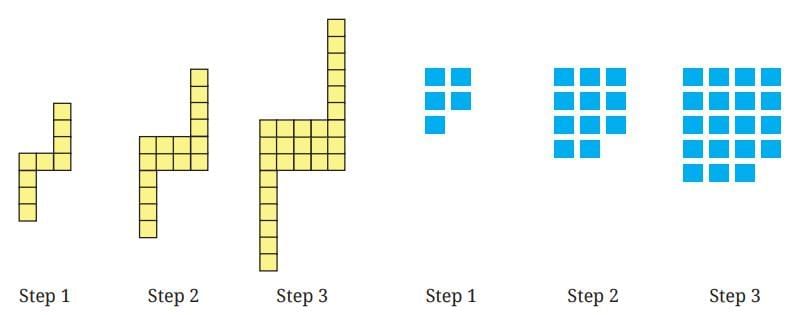 
(i) Draw the next figure in the sequence.
Ans: Next figure in the sequence:
(ii) How many basic units are there in Step 10?
Ans: Step 1 has (1 + 1)2 + 1 or 5 squares
Step 2 has (2 + 1 )2 + 2 or 11 squares
Step 3 has (3 + 1)2 + 3 or 19 squares
Hence step 10 has (10 + 1)2 + 10 or 131 squares
(iii) Write an expression to describe the number of basic units in Step y.
Ans: In 1stfigure:-
Step 1:- (1 + 2)2 = 9
Step 2:- (2 + 2)2 = 16
Step 3:- (3 + 2)2 = 25
→ Step y:- (y + 2)2
In 2nd figure:-
Step 1:- (1+1)2+ 1 = 5
Step 2:- (2+1)2+ 2 = 16
Step 3:- (3 + 1)2+ 3= 25
→ Step y:- (y + 1)2 + y
|
26 videos|133 docs|11 tests
|
FAQs on We Distribute, Yet Things Multiply NCERT Solutions - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is the significance of the concept "We Distribute, Yet Things Multiply" in mathematics? |  |
| 2. How does the distributive property apply to real-life situations? | |
| 3. Can you provide an example of using the distributive property in algebraic expressions? | |
| 4. What role does multiplication play in the context of the given article? | |
| 5. How can students improve their understanding of the distributive property and multiplication? | |
We Distribute
,video lectures
,Viva Questions
,practice quizzes
,Important questions
,shortcuts and tricks
,study material
,Extra Questions
,Yet Things Multiply NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash)
,past year papers
,Objective type Questions
,Yet Things Multiply NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash)
,Exam
,Summary
,Semester Notes
,Yet Things Multiply NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash)
,mock tests for examination
,MCQs
,Free
,We Distribute
,Previous Year Questions with Solutions
,ppt
,Sample Paper
,We Distribute
;
NCERT Solutions: We Distribute, Yet Things Multiply Free PDF Download
Importance of NCERT Solutions: We Distribute, Yet Things Multiply
NCERT Solutions: We Distribute, Yet Things Multiply Notes
NCERT Solutions: We Distribute, Yet Things Multiply Class 8 Questions
Study NCERT Solutions: We Distribute, Yet Things Multiply on the App
|
© EduRev
|
Education Revolution
|
|
