Proportional Reasoning-1 NCERT Solutions | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Page 162 |

|
| Page 163-166 |

|
| Page 167 |

|
| Page 170-171 |

|
| Page 175 |

|
| Page 176-177 |

|
Page 162
Example 1:
(i) Are the ratios 3 : 4 and 72 : 96 proportional?
(ii) What is the HCF of 72 and 96?
Ans:
(i) HCF of 3 and 4 = 1
∴ Ratio 3/4 is in its simplest form.
HCF of 72 and 96 = 24 (∵ 72 = 24 × 3 and 96 = 24 × 4)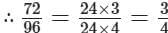
∴ Ratio 72/96 in its simplest form is 3/4.
∴ Ratios 3 : 4 and 72 : 96 are proportional, because both ratios in their simplest form are the same.
(iii) HCF of 72 and 96 is equal to 24.
Example 2: Kesang wanted to make lemonade for a celebration. She made 6 glasses of lemonade in a vessel and added 10 spoons of sugar to the drink. Her father expected more people to join the celebration. So he asked her to make 18 more glasses of lemonade.
Ans: Number of glasses of lemonade = 6
Number of spoons of sugar = 10
∴ Ratio of glasses of lemonade to spoon of sugar = 6/10 = 3/5 = 3 : 5
In the second case, the number of glasses of lemonade = 18
Let the number of spoons of sugar = x
∴ Ratio of glasses of lemonade to spoons of sugar = 18/x = 18 : x
Since sweetness is the same, the ratios 3 : 5 and 18 : x are in proportion.
∴ 3/5 = 18/x
⇒ 3x = 5 × 18 = 90
⇒ x = 90/3 = 30
∴ Number of spoons of sugar = 30.
Number of glasses of lemonade in the I case = 6
Number of glasses of lemonade in the II case = 18
∴ Factor of change = 18/6 = 3
Page 163-166
Example 3: Nitin and Hari were constructing a compound wall around their house. Nitin was building the longer side, 60 ft in length, and Hari was building the shorter side, 40 ft in length. Nitin used 3 bags of cement but Hari used only 2 bags of cement. Nitin was worried that the wall Hari built would not be as strong as the wall he built because she used less cement.
Is Nitin correct in his thinking?
Ans: 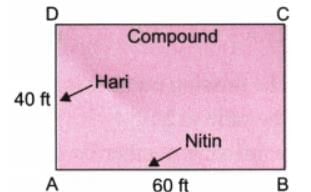 For Nitin, the ratio of the length of the wall to the number of bags of cement = 60/3 =20/1
For Nitin, the ratio of the length of the wall to the number of bags of cement = 60/3 =20/1
For Hari, the ratio of the length of the wall to the number of bags of cement = 40/2 =20/1
∴ Ratios in simplest form are equal.
∴ Ratios 60 : 3 and 40 : 2 are in proportion.
∴ Walls are equally strong.
∴ Nitin is not correct in his thinking.
Note: Both ratios show that 1 bag of cement is required for a wall of 20 ft.
Example 4: In my school, there are 5 teachers and 170 students. The ratio of teachers to students in my school is 5 : 170. Count the number of teachers and students in your school. What is the ratio of teachers to students in your school? Write it below.
Ans:
In the given school, there are 5 teachers and 170 students.
∴ Ratio of teachers to students = 5/170 =1/34 = 1 : 34
In my school, there are 6 teachers and 213 students.
∴ Ratio of teachers to students = 6/213 = 1/35.5 = 1 : 35.5
∴ The teacher-to-student ratios 5 : 170 and 6 : 213 are not proportional.
∴ The teacher-to-student ratio in my school is not proportional to that in the given school.
Example 5: Measure the width and height (to the nearest cm) of the blackboard in your classroom. What is the ratio of width to height of the blackboard?
Can you draw a rectangle in your notebook whose width and height are proportional to the ratio of the blackboard?
Compare the rectangle you have drawn to those drawn by your classmates. Do they all look the same?
Ans:
Let the width and height of the blackboard in my classroom be 300 cm and 150 cm, respectively.
∴ Ratio of width to height = 300/150 cm = 2/1 Draw a line AB equal to 6 cm.
Draw a line AB equal to 6 cm.
Let the height of the rectangle be x cm, so that the width and height of the rectangle are proportional to the ratio of the blackboard.
∴ 2 : 1 :: 6 : x
⇒ 2/1 = 6/x
⇒ 2x = 6
⇒ x = 3
∴ The height of the rectangle is 3 cm.
Draw AD and BC perpendicular to AB and of length 3 cm. Join CD.
ABCD is the required rectangle.
Comparing the rectangles drawn by other classmates, I find that the ratios of width and height of all rectangles drawn by other classmates are proportional. Their rectangle are all similar, but they do not look the same.
Example 6: When Neelima was 3 years old, her mother was 10 times her age. What is the ratio of Neelima’s age to her mother’s age? What would be the ratio of their ages when Neelima is 12 years old? Would it remain the same?
Ans:
Age of Neelima = 3 years
Mother’s age is 10 times the age of Neelima.
∴ Age of mother = 10 × 3 = 30 years
∴ Ratio of Neelima’s age to her mother’s age = 3/30 = 1/10 = 1 : 10
Now, Neelima is 12 years old.
Age of Neelima is 12 years, after 12 – 3 = 9 years.
After 9 years, age of mother = 30 + 9 = 39 years
∴ Ratio of Neelima’s age to her mother’s age = 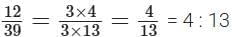
Remark: It must be noted that ratios 14 : 13 are not in proportion.
The rule is that when a fixed number k is added (or subtracted) from a ratio a : b, then the new ratio a + k : b + k may or may not be in proportion with the original ratio a : b.
In other words, a : b :: a + k : b + k may not be true.
Example 7: Fill in the missing numbers for the following ratios that are proportional to 14 : 21.
(i) ____ : 42
(ii) 6 : ____
(iii) 2 : ____
What factor should we multiply 14 by to get 6? Can it be an integer? Or should it be a fraction? (Page 164)
Ans:
The given ratio is 14 : 21.
(i) The ratio is ____ : 42.
Let the missing number be x.
14 : 21 :: x : 42
⇒ 14/21 = x/42
⇒ 2/3 = x/42
⇒ 3x = 2 × 42 = 84
⇒ x = 28
∴ The missing number is 28.
(ii) The ratio is 6 : ____
Let the missing number be x.
∴ 14 : 21 :: 6 : x
⇒ 14/21 = 6/x
⇒ 2/3 = 6/4x
⇒ 2x = 3 × 6 = 18
⇒ x = 9
∴ The missing number is 9.
(iii) The ratio is 2 : ____
Let the missing number be x.
∴ 14 : 21 :: 2 : x
⇒ 14/21 = 2/x
⇒ 2/3 = 2/x
⇒ 2x = 6
⇒ x = 3
∴ The missing number is 3.
Second Part: Ratios under consideration are 14 : 21 and 6 : ____
Now, 6/14 =3/7 and 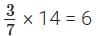
∴ 14 should be multiplied by 3/7 to get 6.
∴ Required factor = 3/7
∴ Missing term in the ratio 6 : ____ is 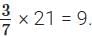
∴ The ratio 6 : ____ is 6 : 9.
The factor here is 3/7 and this is a fraction.
Example 8: Filter coffee is a beverage made by mixing coffee decoction with milk. Manjunath usually mixes 15 mL of coffee decoction with 35 mL of milk to make one cup of filter coffee in his coffee shop. In this case, we can say that the ratio of coffee decoction to milk is 15 : 35. If customers want ‘stronger’ filter coffee. Manjunath mixes 20 mL of the decoction with 30 mL of milk. The ratio here is 20 : 30. Why is this coffee stronger? (i) And when they want ‘lighter’ filter coffee, he mixes 10 mL of coffee and 40 mL of milk, making the ratio 10 : 40. Why is this coffee lighter?
(i) And when they want ‘lighter’ filter coffee, he mixes 10 mL of coffee and 40 mL of milk, making the ratio 10 : 40. Why is this coffee lighter?
(ii) The following table shows the different ratios in which Manjunath mixes coffee decoction with milk. Write in the last column if the coffee is stronger or lighter than the regular coffee.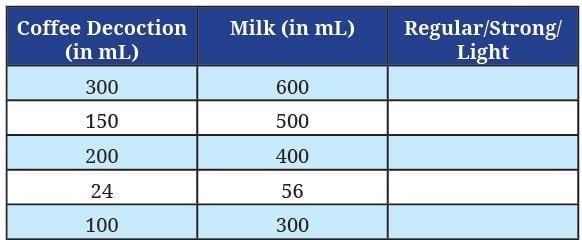 Ans:
Ans:
In one cup of regular filter coffee: Coffee decoction = 15 mL
Milk = 35 mL
∴ Ratio of coffee decoction to milk = 15 : 35 = 3 : 7
Here, 3 + 7 = 10
∴ Coffee decoction in 10 mL filter coffee = 3 mL
∴ Coffee decoction in 100 mL filter coffee =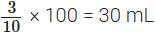
In one cup of stronger filter coffee:
Coffee decoction = 20 mL
Milk = 30 mL
∴ Ratio of coffee decoction to milk = 20 : 30 = 2 : 3
Here, 2 + 3 = 5.
∴ Coffee decoction in 5 mL filter coffee = 2 mL
∴ Coffee decoction in 100 mL filter coffee 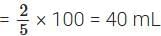
Since 40 mL > 30 mL, the latter coffee is stronger.
(i) In a cup of lighter filter coffee:
Coffee decoction = 10 mL
Milk = 40 mL
∴ Ratio of coffee decoction to milk = 10 : 40 = 1 : 4
Here, 1 + 4 = 5.
∴ Coffee decoction in 5 mL filter coffee = 1 mL
∴ Coffee decoction in 100 mL filter coffee 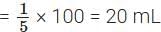
Since 20 mL < 30 mL, the third type of filter coffee is lighter.
(ii) 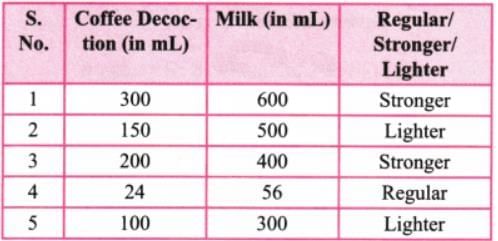
S.No.1. Here 300 + 600 = 900
∴ Coffee decoction in 900 mL filter coffee = 300
∴ Coffee decoction in 100 mL filter coffee = 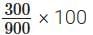
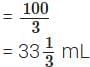
Since 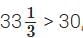 this filter coffee is stronger.
this filter coffee is stronger.
S.No.2. Here 150 + 500 = 650
∴ Coffee decoction in 650 mL filter coffee = 150
∴ Coffee decoction in 100 mL filter coffee = 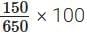
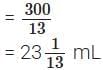
Since 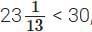 this filter coffee is lighter.
this filter coffee is lighter.
S.No. 3. Here 200 + 400 = 600
∴ Coffee decoction in 600 mL filter coffee = 200
∴ Coffee decoction in 100 mL filter coffee = 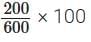

Since 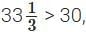 this filter coffee is stronger.
this filter coffee is stronger.
S.No. 4. Here 24 + 56 = 80
∴ Coffee decoction in 80 mL filter coffee = 24 mL
∴ Coffee decoction in 100 mL filter coffee 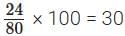
Since 30 = 30, this filter coffee is regular.
S.No. 5. Here 100 + 300 = 400
∴ Coffee decoction in 400 mL filter coffee = 100 mL
∴ Coffee decoction in 100 mL filter coffee = 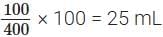
Since 25 < 30, this filter coffee is lighter.
Figure it Out
Q1. Circle the following statements of proportion that are true.
(i) 4 : 7 :: 12 : 21
(ii) 8 : 3 :: 24 : 6
(iii) 7 : 12 :: 12 : 7
(iv) 21 : 6 :: 35 : 10
(v) 12 : 18 :: 28 : 12
(vi) 24 : 8 :: 9 : 3
Ans:
(i) 4 : 7 :: 12 : 21.
This is true if 4/7 = 12/21
or if 4/7 = 4/7, which is true.
∴ The given statement is true.
(ii) 8 : 3 :: 24 : 6.
This is true if 8/3 = 24/6
or if 8/3 = 4 , which is false.
∴ The given statement is not true.
(iii) 7 : 12 :: 12 : 7.
This is true if 7/12 = 12/7, which is false.
∴ The given statement is not true.
(iv) 21 : 6 :: 35 : 10.
This is true if 21/6 = 35/10
or if 7/2 = 7/2, which is true.
∴ The given statement is true.
(v) 12 : 18 :: 28 : 12.
This is true if 12/18 = 28/12
or if 2/3 = 7/3
or 2 = 7, which is false.
∴ The given statement is not true.
(vi) 24 : 8 :: 9 : 3.
This is true if 24/8 = 9/3
Or if 3 = 3, which is true.
∴ The given statement is true.
Q2. Give 3 ratios that are proportional to 4 : 9.
______ : ______ ______ : ______ ______ : ______
Ans:
The given ratio is 4 : 9.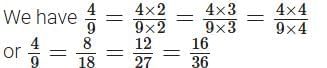
∴ 4 : 9 :: 8 : 18, 4 : 9 :: 12 : 27, and 4 : 9 :: 16 : 36
∴ Ratios 8 : 18, 12 : 27 and 16 : 36 are proportional to the given ratio 4 : 9.
Q3. Fill in the missing numbers for these ratios that are proportional to 18 : 24.
3 : ______, 12 : ______, 20 : ______, 27 : ______
Ans: 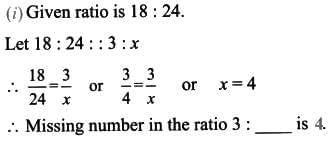

Q4. Look at the following rectangles. Which rectangles are similar to each other? You can verify this by measuring the width and height using a scale and comparing their ratios.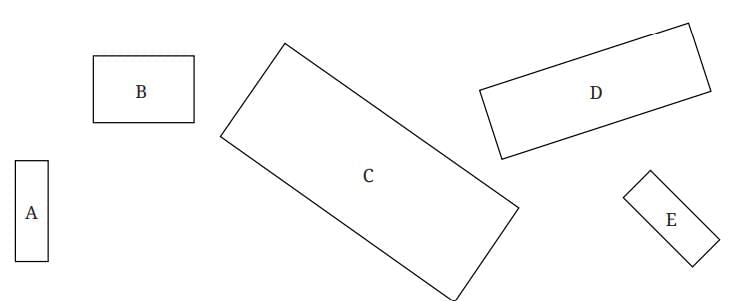 Ans:
Ans:
Using a scale, we measure the width and height of given rectangles.
Here, the ratio ‘Width : Height’ for given rectangles A, B, C, D, and E are respectively 1 : 3, 3 : 2, 9 : 4, 7 : 2 and 3 : 1.
These ratios are all distinct. The ratios of A and E are 1 : 3 and 3 : 1 respectively.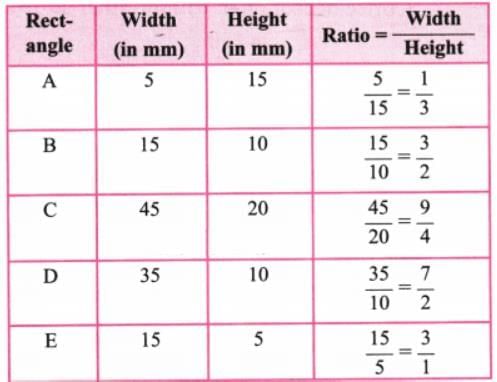 ∴ For A and E, one side is 3 times the other side.
∴ For A and E, one side is 3 times the other side.
∴ Only rectangles A and E are similar.
Q5. Look at the following rectangle. Can you draw a smaller rectangle and a bigger rectangle with the same width to height ratio in your notebooks? Compare your rectangles with your classmates’ drawings. Are all of them the same? If they are different from yours, can you think why? Are they wrong? Ans:
Ans:
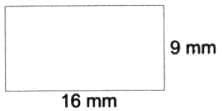
For the given rectangle;
Width = 32 mm and height = 18 mm
∴ Ratio is 32 : 18.
We shall draw smaller and bigger rectangles and similar to the given rectangle by considering different ‘factors of change’.
Let the factor of change be 1/2.
∴ New width = 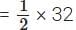 = 16 mm
= 16 mm
and New height =  = 9 mm
= 9 mm
A new, similar rectangle is shown in the figure.
Let ‘factor of change’ be 2.
∴ New width = 2 × 32 = 64 mm and new height = 2 × 18 = 36 mm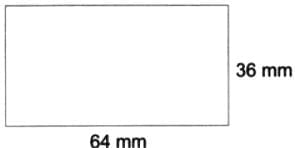 A new, similar rectangle is shown in the figure. The rectangles drawn by other classmates are all different, but they are all similar to the given rectangle.
A new, similar rectangle is shown in the figure. The rectangles drawn by other classmates are all different, but they are all similar to the given rectangle.
Q6. The following figure shows a small portion of a long brick wall with patterns made using coloured bricks. Each wall continues this pattern throughout the wall. What is the ratio of grey bricks to coloured bricks? Try to give the ratios in their simplest form.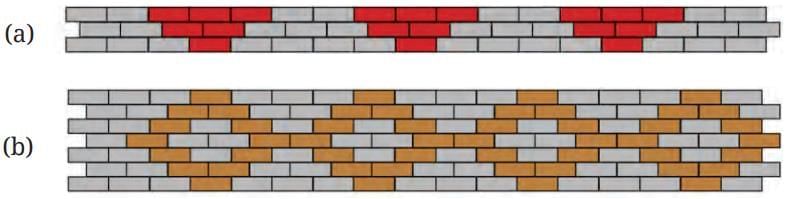
Ans:
(a) We consider one set of patterns in the given wall.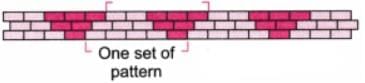
Number of grey bricks in one set of pattern = 2 + 3 + 4 = 9
Number of coloured bricks in one set of pattern = 3 + 2 + 1 = 6
∴ Ratio of grey bricks to coloured bricks = 9 : 6
We have 9 : 6 = 3 : 2
∴ Ratio in the simplest form = 3 : 2
(b) We use one set of patterns on the given wall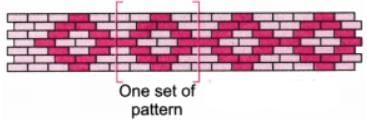 Number of grey bricks in one set of pattern
Number of grey bricks in one set of pattern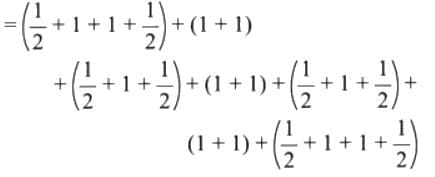 = 3 + 2 + 2 + 2 + 2 + 2 + 3
= 3 + 2 + 2 + 2 + 2 + 2 + 3
= 16
Number of coloured bricks in one set of pattern = 1 + (1 + 1) + (1 + 1) + (1 + 1) + (1 + 1) + (1 + 1) + 1
= 1 + 2 + 2 + 2 + 2 + 2 + 1
= 12
∴ Ratio of grey bricks to coloured bricks = 16 : 12
We have 16 : 12 = 4 : 3
∴ Ratio in the simplest form = 4 : 3.
Page 167
Q7. Let us draw some human figures. Measure your friend’s body—the lengths of their head, torso, arms, and legs. Write the ratios as mentioned below—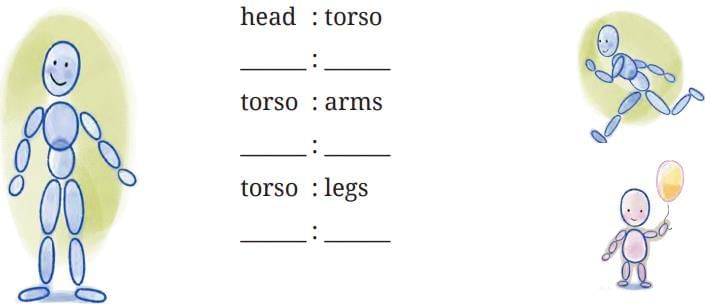
Now, draw a figure with head, torso, arms, and legs with equivalent ratios as above.
Ans: My friend’s body measurements:
(i) Head = 22 cm
(ii) Torso (neck to hip) = 50 cm
(iii) Arms (shoulder to fingertip) = 60 cm
(iv) Legs (hip to foot) = 80 cm
1. Head : Torso = 22 : 50
Simplify by dividing both by 2 → 11 : 25.
2. Torso : Arms = 50 : 60
Simplify by dividing both by 10 → 5 : 6.
3. Torso : Legs = 50 : 80
Simplify by dividing both by 10 → 5 : 8.
So the ratios are:
- Head : Torso = 11 : 25
- Torso : Arms = 5 : 6
- Torso : Legs = 5 : 8
Example 8: For the mid-day meal in a school with 120 students, the cook usually makes 15 kg of rice. On a rainy day, only 80 students came to school. How many kilograms of rice should the cook make so that the food is not wasted?
The ratio of the number of students to the amount of rice needs to be proportional. So, 120 : 15 :: 80 : ?
What is the factor of change in the first term?
Ans:
For 120 students, the rice required is 15 kg.
Let x kg of rice be required for 80 students.
∴ Ratios 120 : 15 and 80 : x are in proportion.
∴ 120 : 15 :: 80 : x
⇒ 120/15 = 80/x
⇒ x = 10
∴ 10 kg of rice is required.
Also, factor of change in the first term = 80/120 = 2/3
Alternative Method:
Factor of change in second term = x/15
Since the quality of food is the same, we have 2/3 = x/15
⇒ 3x = 30
⇒ x = 10
∴ 10 kg of rice is required.
Example 9: (i) A car travels 90 km in 150 minutes. If it continues at the same speed, what distance will it cover in 4 hours?
If it continues at the same speed, the ratio of the time taken should be proportional to the ratio of the distance covered.
(ii) 150 : 90 :: 4 : x
Is this the right way to formulate the question?
(iii) How can you find the distance covered in 240 minutes?
Ans:
(i) We have, 4 hours = 4 × 60 = 240 minutes
In 150 minutes, the distance covered = 90 km
Let x km be covered in 4 hours, i.e., in 240 minutes.
∴ The ratios 150 : 90 and 240 : x are in proportion.
∴ 150 : 90 :: 240 : x
(ii) Since units must be the same in comparing ratios, the given proportion 150 : 90 :: 4 : ? is meaningless.
We have 4 hours = 240 minutes
∴ The proportion 150 : 90 :: 240 : ? is correct.
(iii) We have 150 : 90 :: 240 : x
⇒ 150/90 = 240x
⇒ 5/3 = 240/x
⇒ 5x = 3 × 240
⇒ x = 144
∴ Distance covered in 4 hours = 144 km.
Example 10: A small farmer in Himachal Pradesh sells each 200 g packet of tea for ₹ 200. A large estate in Meghalaya sells each 1 kg packet of tea for ₹ 800. Are the weight-to-price ratios in both places proportional? Which tea is more expensive? Why? (Page 169)
Ans:
We have 1 kg = 1000 g
In Himachal Pradesh, 200 g of tea costs ₹ 200.
∴ Ratio of weight to price in Himachal Prdesh = 200 : 200 = 1 : 1
In Meghalaya, 1000 g tea costs ₹ 800.
∴ Ratio of weight to price in Meghalaya = 1000 : 800 = 5 : 4
The ratios 1 : 1 and 5 : 4 are not proportional, because 1/1 ≠ 5/4
Price of 200 g tea in Himachal Pradesh = ₹ 200
Price of 1000 g tea in Himachal Pradesh = 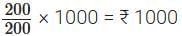
Since 1000 > 800, tea is more expensive in Himachal Pradesh.
Page 170-171
Q1. The Earth travels approximately 940 million kilometres around the Sun in a year. How many kilometres will it travel in a week?
Ans:
We know that:
1 million = 10 lakh = 10,00,000
and 1 year = 365/7 weeks.
940 million kilometres, i.e., 940 × 10,00,000 kilometres, are travelled by the Earth in 1 year, i.e., in 365/7 weeks.
Let the Earth travel x kilometres in 1 week
∴ The ratios 940 × 10,00,000 : 365/7 and x : 1 are in proportion.
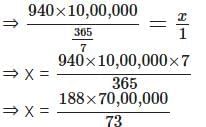
⇒ x = 1,80,27,397 (nearly)
∴ In 1 week, Earth travels nearly 1,80,27,397 kilometres around the Sun.
Q2. A mason is building a house in the shape shown in the diagram. He needs to construct both the outer walls and the inner wall that separates two rooms. To build a wall of 10-feet, he requires approximately 1450 bricks. How many bricks would he need to build the house? Assume all walls are of the same height and thickness.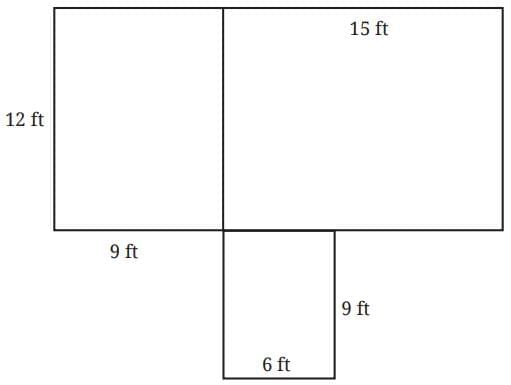 Ans:
Ans:
Number of bricks required for a 10 ft wall =1450
∴ Ratio of length of wall to number of bricks = 10 : 1450
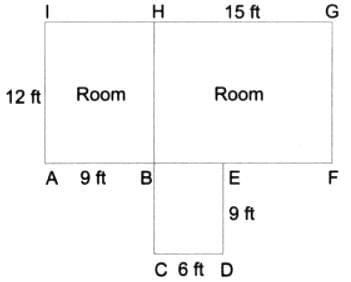 Total length of walls = AI + CH + DE + FG + IG + AF + CD
Total length of walls = AI + CH + DE + FG + IG + AF + CD
= 12 + (9 + 12) + 9 + 12 + (9 + 15) + (9 + 15) + 6
= 108 ft
Let x bricks be required for a 108 ft long wall.
∴ Ratio of length of wall to number of bricks = 108 : x
These ratios are in proportion.
∴ 10 : 1450 :: 108 : x
⇒ 10/1450 = 108x
⇒ 1/145 = 108x
⇒ x = 145 × 108 = 15,660
∴ Number of required bricks = 15,660.
Q: Puneeth’s father went from Lucknow to Kanpur in 2 hours by riding his motorcycle at a speed of 50 km/h. If he drives at 75 km/h, how long will it take him to reach Kanpur? Can we form this problem as a proportion 50 : 2 :: 75 : ____
Would it take Puneeth’s father more time or less time to reach Kanpur? Think about it.
Ans:
Time taken at the speed of 50 km/h = 2 hours
∴ Distance = Speed × Time
= 50 × 2
= 100 km
At speed of 75 km/h, time taken = 100/75 = 4/3 hours
∴ Ratio of speed to time in both cases are 50 : 2 and 75 : 4/3
Here, 50/2 = 25 and 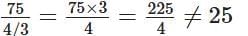
∴ The ratios 50 : 2 and 75 : 4/3 are not in proportion.
∴ We cannot write 50 : 2 :: 75 : 4/3.
At a speed of 75 km/h, Puneeth’s father will take 4/3 hours to reach Kanpur, which is less than 2 hours.
Example 11: Prashanti and Bhuvan started a food cart business near their school. Prashanti invested ₹ 75,000 and Bhuvan invested ₹ 25,000. At the end of the first month, they gained a profit of ₹ 4,000. They decided that they would share the profit in the same ratio as their investment. What is each person’s share of the profit?
Ans:
Investment of Prashanti = ₹ 75,000
Investment of Bhuvan = ₹ 25,000
∴ Ratio of investment = 75000 : 25000 = 3 : 1
Total profit = ₹ 4,000
∴ Share of Prashanti =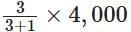
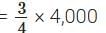
= ₹ 3,000
∴ Share of Bhuvan = 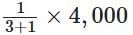
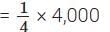
= ₹ 1,000
Verification: ₹ 3,000 + ₹ 1,000 = ₹ 4,000, the total profit.
Example 12: A mixture of 40 kg contains sand and cement in the ratio of 3 : 1. How much cement should be added to the mixture to make the ratio of sand to cement 5 : 2?
Ans:
Ratio of sand and cement = 3 : 1
Weight of mixture = 40 kg
∴ Weight of sand in mixture = 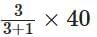
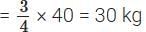
Weight of cement in the mixture = 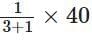
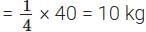
Let the weight of cement in the new mixture be x kg, so that the new ratio is 5 : 2.
∴ Ratios 30 : x and 5 : 2 are in proportion.
⇒ 30/x = 5/2
⇒ 5x = 60
⇒ x = 12
Weight of cement added = 12 kg – 10 kg = 2 kg
Page 175
Q1. Divide ₹4,500 into two parts in the ratio 2 : 3.
Ans:
Given ratio = 2 : 3
Amount to be divided = ₹ 4,500
∴ First part = 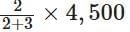
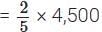
= 2 × 900
= ₹ 1,800
∴ Second part = 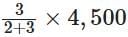
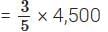
= 3 × 900
= ₹ 2,700
∴ Two parts are ₹ 1,800 and ₹ 2,700.
Verification:
1,800 : 2,700 = 1,800/2,700 = 18/27 = 2/3 = 2 : 3 and 1,800 + 2,700 = 4,500.
Q2: In a science lab, acid and water are mixed in the ratio of 1 : 5 to make a solution. In a bottle that has 240 mL of the solution, how much acid and water does the solution contain?
Ans:
Ratio of acid and water = 1 : 5
Quantity of solution = 240 mL
∴ Quantity of acid = 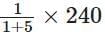
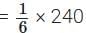
= 40 mL
∴ Quantity of water = 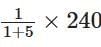
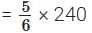
= 200 mL
∴ Quantities of acid and water in the solution are 40 mL and 200 mL.
Verification:
40 : 200 = 40/200 = 1/5 = 1 : 5 and 40 + 200 = 240.
Q3. Blue and yellow paints are mixed in the ratio of 3 : 5 to produce green paint. To produce 40 mL of green paint, how much of these two colours are needed? To make the paint a lighter shade of green, I added 20 mL of yellow to the mixture. What is the new ratio of blue and yellow in the paint?
Ans: Ratio of Blue and yellow paints in mixture = 3 : 5
To produce 40 mL of green paint, quantity of Blue pain needed = 3/(3 + 5) × 40 mL = 3/8 × 40 mL = 15 mL
∴ Quantity of yellow pain needed = 5/8 × 40 mL = 25mL
Now, add 20 mL of yellow to the mixture.
Then, the ratio of blue and yellow in the new mixture =15 : (25 + 20) = 15 : 45 = 1 : 3
Q4. To make soft idlis, you need to mix rice and urad dal in the ratio of 2 : 1. If you need 6 cups of this mixture to make idlis tomorrow morning, how many cups of rice and urad dal will you need?
Ans: Required ratio of rice and urad = 2 : 1 and total quantity of mixture = 6 cups
∴ Amount of rice required = 2/(2 + 1) × 6 = 2/3 × 6 = 4 cups
∴ Amount of urad required = 1/(2 + 1) × 6 = 1/3 × 6 = 2 cups
Q5. I have one bucket of orange paint that I made by mixing red and yellow paints in the ratio of 3 : 5. I added another bucket of yellow paint to this mixture. What is the ratio of red paint to yellow paint in the new mixture?
Ans:
Let the capacity of one bucket be x L.
Ratio of red paint and yellow paint = 3 : 5
∴ Quantity of red paint in the bucket =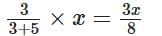
∴ Quantity of yellow paint in the bucket =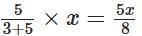
One bucket of yellow paint is added to the mixture.
∴ New quantity of red paint in the mixture = 3x/8
∴ New quantity of yellow paint in the mixture = 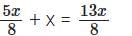
∴ New ratio of red paint and yellow paint in the mixture = 3x/8:13x/8 = 3 : 13
Page 176-177
Q1. Anagh mixes 600 mL of orange juice with 900 mL of apple juice to make a fruit drink. Write the ratio of orange juice to apple juice in its simplest form.
Ans:
Quantity of orange juice = 600 mL
Quantity of apple juice = 900 mL
∴ Ratio of orange juice to apple juice = 600 : 900
Ratio in the simplest form = 600 : 900 = 2 : 3
Q2. Last year, we hired 3 buses for the school trip. We had a total of 162 students and teachers who went on that trip and all the buses were full. This year we have 204 students. How many buses will we need? Will all the buses be full?
Ans:
Number of buses for 162 students and teachers = 3
Since the buses were full, the capacity of 1 bus = 162/3 = 54
∴ Ratio of number of seats to the number of buses is 54 : 1.
We have
54 : 1 = 2(54) : 2(1) = 108 : 2
54 : 1 = 3(54) : 3(1) = 162 : 3
54 : 1 = 4(54) : 4(1) = 216 : 4
∴ Capacity of 4 buses = 216
∴ For 204 students, we shall need 4 buses.
Since 216 – 204 = 12, we have 12 vacant seats in the buses.
Q3. The area of Delhi is 1,484 sq. km and the area of Mumbai is 550 sq. km. The population of Delhi is approximately 30 million and that of Mumbai is 20 million people. Which city is more crowded? Why do you say so?
Ans:
Area of Delhi = 1,484 sq.km
Population of Delhi = 30 million
Area of Mumbai = 550 sq. km
Population of Mumbai = 20 million
∴ Ratio of area to population for Delhi = 1484 : 30
∴ Ratio of area to population for Mumbai = 550 : 20
Factor of change of area = 550/1484 = 0.371 (nearly)
Factor of change of population = 20/30 = 0.667 (nearly)
Since 0.667 > 0.371, Mumbai is more crowded than Delhi.
Alternative Method:
Ratio of area to population for Delhi = 1484 : 30
Let the density of Delhi and Mumbai be the same, and there be x people in Mumbai.
∴ The ratios 1,484 : 30 and 550 : x are in proportion.
∴ 1,484/30 = 550/x
⇒ 1484x = 30 × 550 = 16,500
⇒ x = 16500/1484 = 11.118
There should be 11.118 million people in Mumbai. But the population of Mumbai is 20 million.
∴ Mumbai is more crowded than Delhi.
Q4. A crane of height 155 cm has its neck and the rest of its body in the ratio 4 : 6. For your height, if your neck and the rest of the body also had this ratio, how tall would your neck be? Ans:
Ans:
The ratio of the height of the neck and the height of the rest of the body of a crane is 4 : 6.
My height is 65 inches, i.e., 165 cm.
Let the ratio of the height of my neck and the height of the rest of my body also be 4 : 6.
∴ Height of my neck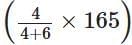 cm = 66 cm
cm = 66 cm
Q5. Let us try an ancient problem from Lilavati. At that time weights were measured in a unit named palas and niskas was a unit of money. “If 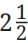 palas of saffron costs 3/7 niskas, O expert businessman! tell me quickly what quantity of saffron can be bought for 9 niskas?”
palas of saffron costs 3/7 niskas, O expert businessman! tell me quickly what quantity of saffron can be bought for 9 niskas?”
Ans:
Here, the unit of weight in palas and the unit of money are niskas.
Cost of 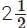 palas of saffron = 37 niskas
palas of saffron = 37 niskas
∴ Ratio of weight to price is 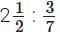
or 5/2 : 3/7
or 35 : 6
Let x palas of saffron be bought for 9 niskas.
∴ Ratio of weight to price is x : 9.
These ratios are in proportion.
∴ 35 : 6 :: x : 9
⇒ 35/6 = x/9
⇒ 6x = 35 × 9
⇒ x = 52.5
∴ 52.5 palas of saffron can be bought for 9 niskas.
Q6. Harmain is a 1-year-old girl. Her elder brother is 5 years old. What will be Harmain’s age when the ratio of her age to her brother’s age is 1 : 2?
Ans:
The ages of Harmain and her brother are 1 year and 5 years.
Let x years, the ratio of their ages be 1 : 2.
Age of Harmain after x years = (1 + x) years.
Age of her brother after x years = (5 + x) years.
∴ After x years, ratio of their ages = 1 + x : 5 + x
The ratios are in proportion.
∴ 1 : 2 :: 1 + x : 5 + x
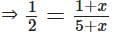
⇒ 5 + x = 2(1 + x)
⇒ 5 + x = 2 + 2x
⇒ 2x – x = 5 – 2
⇒ x = 3
∴ After 3 years, the age of Harmain = 1 + 3 = 4 years.
Verification:
After 3 years, age of her brother = 5 + 3 = 8 years
Also, the ratio of their ages = 4 : 8 = 1 : 2.
Q7. The mass of equal volumes of gold and water are in the ratio 37 : 2. If 1 litre of water is 1 kg in mass, what is the mass of 1 litre of gold?
Ans:
The ratio of masses of gold and water, when their volumes are the same, is 37 : 2.
Mass of 1 litre of water = 1 kg
Let the mass of 1 litre of gold = x kg
∴ With equal volumes, the ratio of masses of gold and water is x : 1.
These ratios are in proportion.
∴ 37 : 2 :: 1 : x
⇒ 37/2 = x/1
⇒ x = 372
Thus, the mass of 1 litre of gold is 37/2 kg.
Q8. It is good farming practice to apply 10 tonnes of cow manure for 1 acre of land. A farmer is planning to grow tomatoes in a plot of size 200 ft by 500 ft. How much manure should he buy?
Ans:
We have 1 ton = 1,000 kg
∴ 10 tonnes = 10 × 1,000 = 10,000 kg
Also, 1 acre = 43,560 sq. ft.
∴ Ratio of cow manure to area of land in kg and sq. ft. = 10,000 : 43,560
Size of plot = 200 ft. by 500 ft.
∴ Area of plot = 200 × 500 = 1,00,000 sq. ft.
Let cow manure be x kg.
∴ Ratio of cow manure to area of plot = x : 1,00,000
These ratios are in proportion.
∴ 10,000 : 43,560 :: x : 1,00,000
⇒ 43,560x = 10,000 × 1,00,000 = 1,00,00,00,000

⇒ x = 22956.84
∴ Required cow manure = 22956.84 kg = 22.95684 tonnes.
Q9. A tap takes 15 seconds to fill a mug of water. The volume of the mug is 500 mL. How much time does the same tap take to fill a bucket of water if the bucket has a 10-litre capacity?
Ans:
Time taken by the tap for 500 mL of water = 15 seconds
∴ Ratio of volume to time = 500 : 15
We know 1 litre = 1,000 mL
10 litre = 10 × 1,000 = 10,000 mL
Let the time taken to fill a bucket of 10,000 mL be x seconds.
∴ Ratio of volume to time = 10,000 : x
These ratios are proportional.
∴ 500 : 15 :: 10,000 : x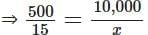
⇒ 500x = 1,50,000
⇒ x = 300
∴ Time to fill bucket = 300 seconds
= 300/60 minutes
= 5 minutes.
Q10. One acre of land costs ₹15,00,000. What is the cost of 2,400 square feet of the same land?
Ans:
We know that 1 acre = 43,560 square feet.
∴ Cost of 43,560 sq. ft. land = ₹ 15,00,000
∴ Ratio of area of land to cost = 43,560 : 15,00,000
Let the cost of 2,400 sq. ft. of land be ₹ x.
∴ Ratio of area of land to cost = 2,400 : x
These ratios are proportional.
∴ 43,560 : 15,00,000 :: 2,400 : x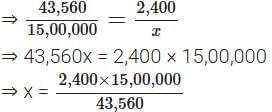
⇒ x = 82,664.63
∴ Cost of land = ₹ 82,664.63.
Q11. A tractor can plough the same area of a field 4 times faster than a pair of oxen. A farmer wants to plough his 20-acre field. A pair of oxen takes 6 hours to plough an acre of land. How much time would it take if the farmer used a pair of oxen to plough the field? How much time would it take him if he decides to use a tractor instead?
Ans:
Ratio of efficiency of a tractor to a pair of oxen = 4 : 1
Time taken by a pair of oxen to plough 1 acre of field = 6 hours
∴ Time taken by a tractor to plough 1 acre field = 6/4 = 1.5 hours
∴ Time taken by a pair of oxen to plough 20 20-acre field = 20 × 6 = 120 hours
∴ Time taken by a tractor to plough a 20-acre field = 20 × 1.5 = 30 hours
Q12. The ₹10 coin is an alloy of copper and nickel called ‘cupro-nickel’. Copper and nickel are mixed in a 3 : 1 ratio to get this alloy. The mass of the coin is 7.74 grams. If the cost of copper is ₹906 per kg and the cost of nickel is ₹1,341 per kg, what is the cost of these metals in a ₹10 coin?
Ans:
Ratio of copper and nickel in ₹ 10 coin = 3 : 1
Mass of one ₹ 10 coin = 7.74 grams
∴ Mass of copper in one ₹ 10 coin = 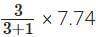
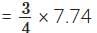
= 5.805 grams
Mass of nickel in one ₹ 10 coin = 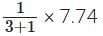
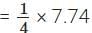
= 1.935 grams
Cost of 1 kg copper = ₹ 906
∴ Cost of 1000 grams of copper = ₹ 906
∴ Cost of 5.805 grams copper = 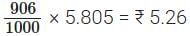
Cost of 1 kg nickel = ₹ 1341
∴ Cost of 1000 grams of nickel = ₹ 1341
∴ Cost of 1.935 grams nickel = 
∴ In one ₹ 10 coin, the cost of copper and the cost of nickel are respectively ₹ 5.26 and ₹ 2.59.
|
26 videos|133 docs|11 tests
|
FAQs on Proportional Reasoning-1 NCERT Solutions - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is proportional reasoning and how is it used in everyday life? |  |
| 2. How can I identify proportional relationships in a table of values? |  |
| 3. What are some common mistakes students make when solving proportional reasoning problems? |  |
| 4. Can you provide examples of real-world problems that involve proportional reasoning? |  |
| 5. What strategies can help improve my understanding of proportional reasoning? |  |















