Important Formulas: Fractions | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
Equivalent Fractions
Two fractions are equivalent if they represent the same value or proportion.
Example: 1/2 = 2/4 = 3/6
Rule: Multiply or divide both numerator and denominator by the same number to get an equivalent fraction.
Example: 3/5 × (2/2) = 6/10
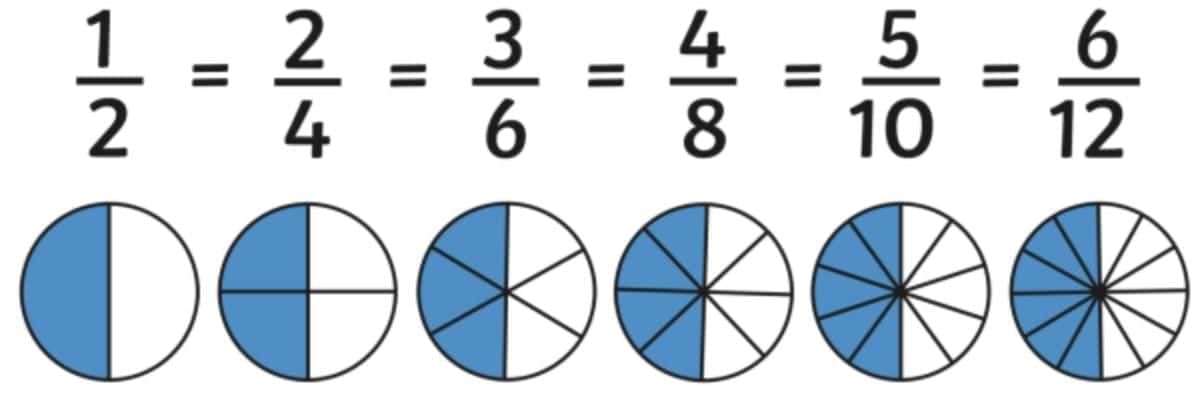
Simplest Form of a Fraction
A fraction is said to be in its simplest form when the numerator and denominator have no common factors except 1.
To simplify: Divide both numerator and denominator by their Greatest Common Divisor (GCD).
Example: 12/18 → divide numerator and denominator by 6 → 2/3
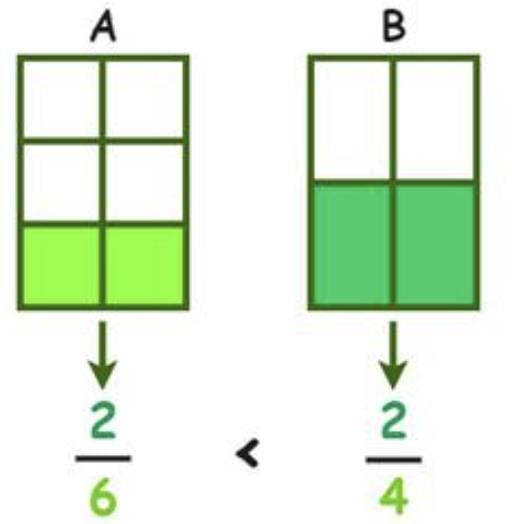
Comparing Fractions
(a) Same Denominator: Compare numerators directly.
Example: 3/7 and 5/7 → 5/7 is greater.
(b) Same Numerator: Compare denominators. Smaller denominator means larger fraction.
Example: 2/3 and 2/5 → 2/3 is greater.
(c) Different Denominators: Convert to equivalent fractions with a common denominator.
Example: Compare 3/4 and 5/6.
LCM of 4 and 6 is 12.
3/4 = 9/12, 5/6 = 10/12 → 10/12 is greater, so 5/6 is greater.
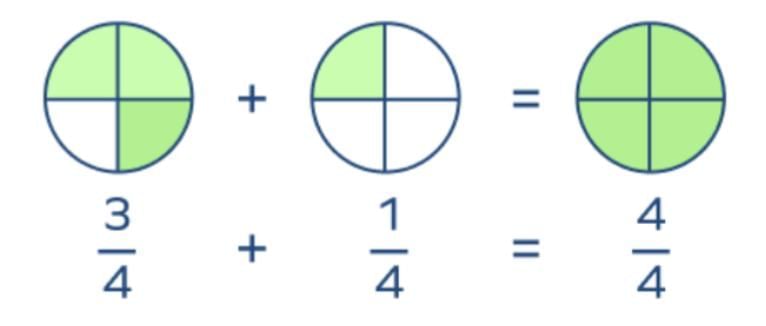
Addition of Fractions
(a) Same Denominator: Add numerators, keep the denominator.
Example: 2/7 + 3/7 = 5/7
Different Denominators:
Step 1: Find LCM of denominators.
Step 2: Convert fractions to equivalent fractions with same denominator.
Step 3: Add numerators, keep denominator.
Example: 2/3 + 5/6
LCM of 3 and 6 = 6
2/3 = 4/6
4/6 + 5/6 = 9/6 = 3/2= 1½
Subtraction of Fractions
Same process as addition, but subtract numerators.
Example: 5/6 – 1/4
Solution:
LCM of 6 and 4 = 12
5/6 = 10/12, 1/4 = 3/12
10/12 – 3/12 = 7/12
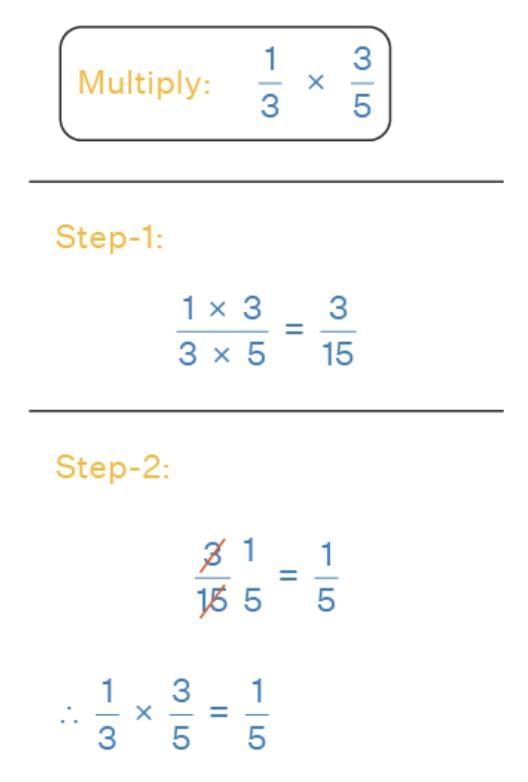
Multiplication of Fractions
Multiply numerators with numerators and denominators with denominators.
Example: 2/3 × 4/5 = (2×4)/(3×5) = 8/15
Simplify if possible.
Division of Fractions
Rule: Multiply the first fraction by the reciprocal (inverse) of the second fraction.
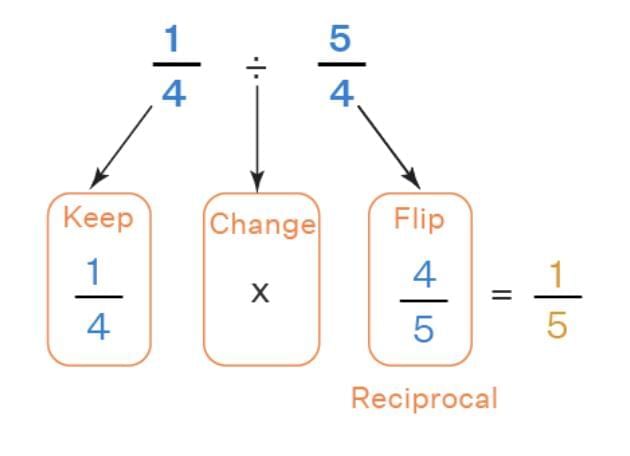
Example: 3/4 ÷ 2/5 = 3/4 × 5/2 = 15/8
Mixed Numbers and Improper Fractions
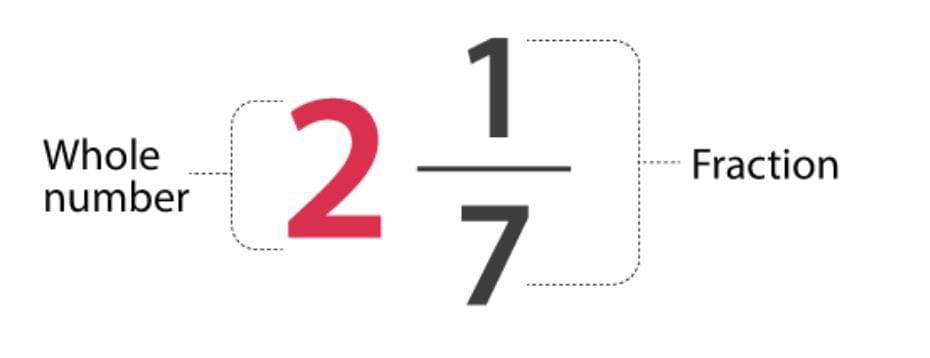
(a) Mixed Number → Improper Fraction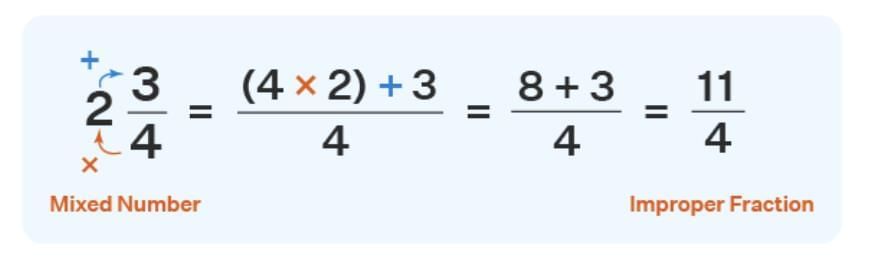
Formula: (Whole number × denominator) + numerator, all over denominator.
Example: 3 2/5 = (3×5 + 2)/5 = 17/5
(b) Improper Fraction → Mixed Number
Divide numerator by denominator.
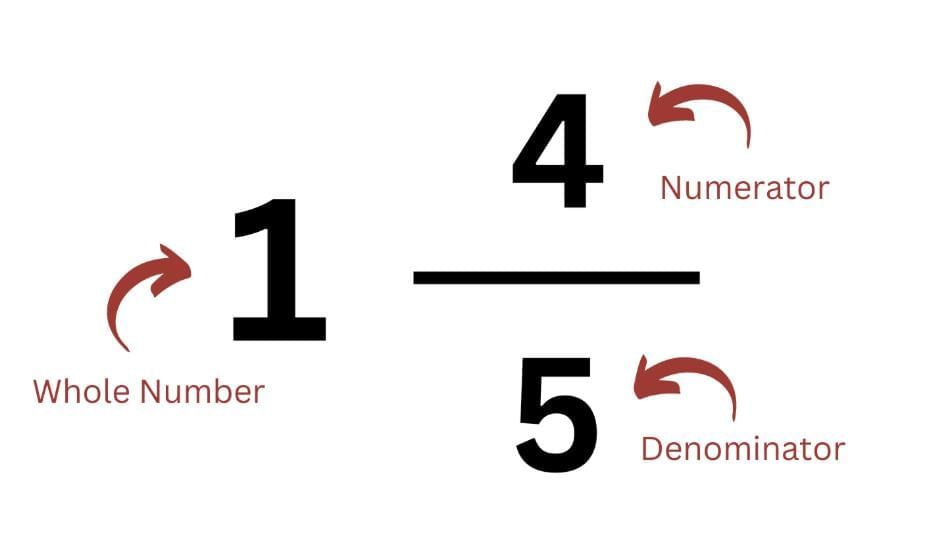
Example: 22/7 = 3 (whole) and remainder 1 → 3 1/7
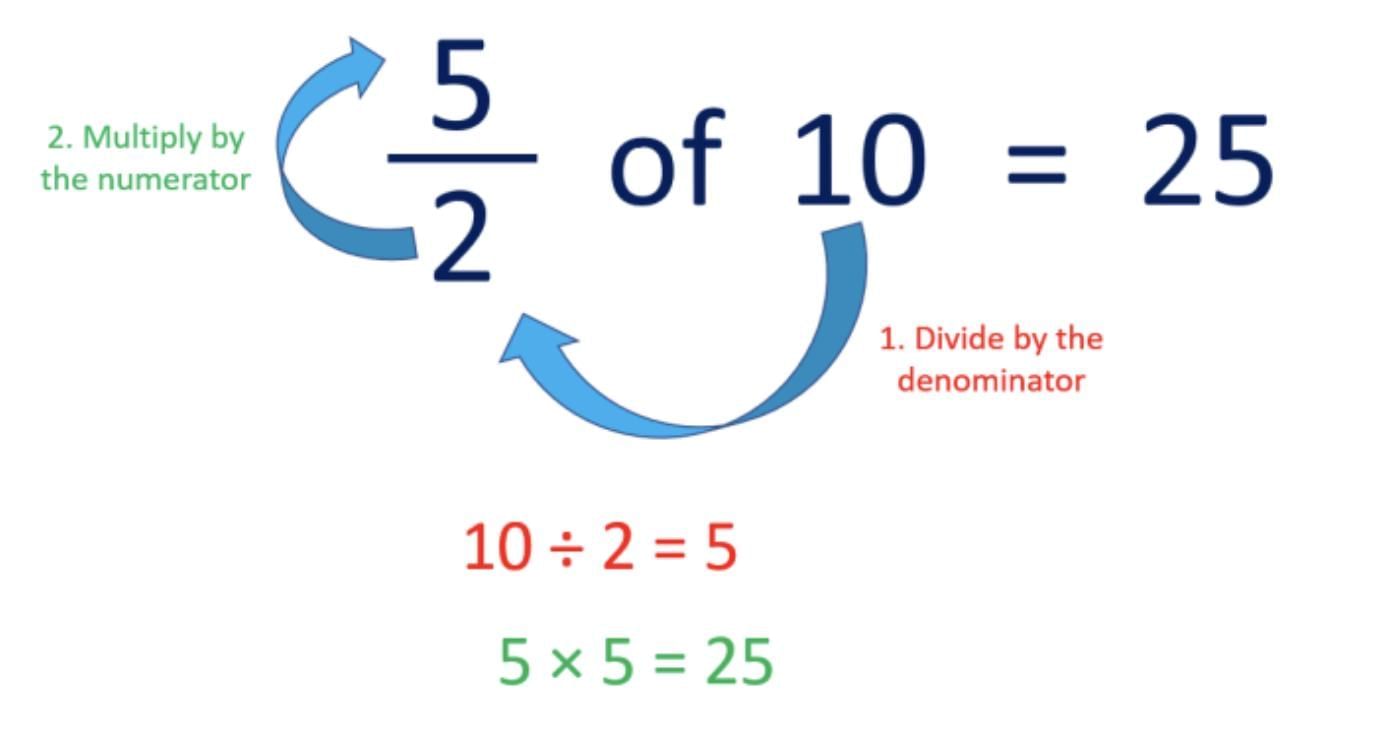
Fraction of a Number
Multiply the number with the fraction.
Example: 2/5 of 50 = (2/5) × 50 = 20
Rule of Signs in Fractions
Positive ÷ Positive = Positive
Negative ÷ Negative = Positive
Positive ÷ Negative = Negative
Negative ÷ Positive = Negative
Properties of Fractions
A fraction always represents a part of a whole.
If numerator < denominator → Proper fraction (value < 1).
If numerator > denominator → Improper fraction (value > 1).
If numerator = denominator → Value = 1.
Fractions can always be reduced to lowest terms.
|
35 videos|318 docs|7 tests
|
FAQs on Important Formulas: Fractions - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are equivalent fractions and how can they be identified? |  |
| 2. How do you simplify a fraction to its simplest form? |  |
| 3. What is the process for comparing two fractions? |  |
| 4. How do you add or subtract fractions with different denominators? |  |
| 5. What are mixed numbers and improper fractions, and how can they be converted from one to the other? |  |
















