Important Formulas: Animal Jumps | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
| Table of contents |

|
| Introduction |

|
| Factors |

|
| Common Factors |

|
| Prime and Composite Numbers |

|
| Multiples |

|
| Common Multiples |

|
| Divisibility Rules |

|

Introduction
Numbers follow special patterns.
Factors break numbers into smaller exact parts.
Multiples show how numbers grow bigger when multiplied.
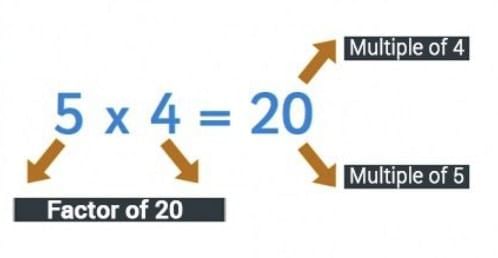
Learning factors and multiples makes it easier to understand divisibility, prime numbers, and patterns in mathematics.
Factors
A factor of a number divides it exactly without leaving a remainder.
If a × b = N, then both a and b are factors of N.
Examples
Factors of 8:
1 × 8 = 8, 2 × 4 = 8
∴ Factors = 1, 2, 4, 8
Rules
Every number has at least two factors: 1 and the number itself.
Factors are always less than or equal to the number.
Factors come in pairs (factor pairs).
Finding Factors
Start with 1 and the number itself.
Check each number in between.
If the division leaves no remainder, it is a factor.
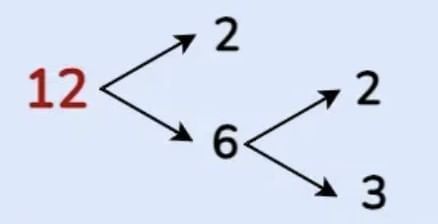
Common Factors
If two or more numbers share the same factor → common factor.
Example:
Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 18 = 1, 2, 3, 6, 9, 18
Common factors = 1, 2, 3, 6
Another Example:

- Common factors = 1, 2, 3, 6
Prime and Composite Numbers
Prime Numbers → Numbers with exactly two factors: 1 and itself.
Example: 13 (factors: 1, 13)
Composite Numbers → Numbers with more than two factors.
Example: 4 (factors: 1, 2, 4)
Special Case:
1 is neither prime nor composite.
Multiples
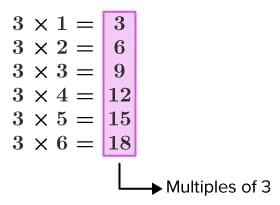
A multiple of a number = product of the number × any counting number.
Example: Multiples of 3:
3, 6, 9, 12, 15, 18, …
Rules
Every number is a multiple of 1.
The smallest multiple of a number is the number itself.
Multiples are infinite.
Every multiple is greater than or equal to the number.
Finding Multiples
Multiply the number by 1, 2, 3, 4, …
Common Multiples
When two or more numbers share a multiple → common multiple.
Example:
Multiples of 3 = 3, 6, 9, 12, 15, …
Multiples of 4 = 4, 8, 12, 16, …
Common multiples = 12, 24, 36, …
Another Example:
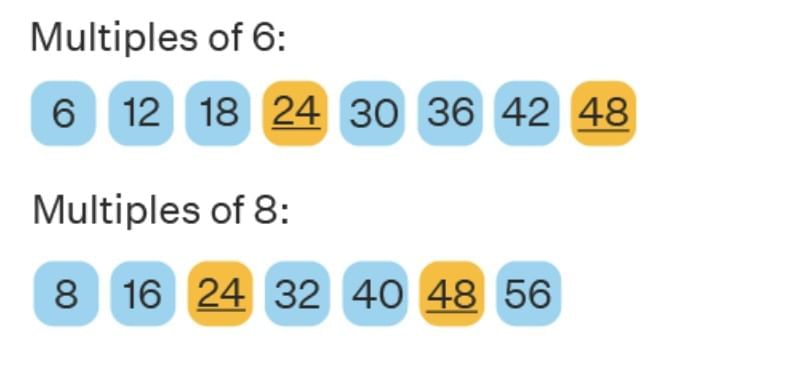
Common multiples = 24, 48, …
Divisibility Rules

Quick tests to check divisibility without long division:
By 2 → Last digit 0, 2, 4, 6, 8
By 3 → Sum of digits divisible by 3
By 4 → Last two digits divisible by 4
By 5 → Last digit 0 or 5
By 6 → Divisible by both 2 and 3
By 8 → Last three digits divisible by 8
By 9 → Sum of digits divisible by 9
By 10 → Last digit 0
By 11 → (Sum of odd place digits − sum of even place digits) divisible by 11
By 25 → Last two digits divisible by 25
|
35 videos|322 docs|7 tests
|
FAQs on Important Formulas: Animal Jumps - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are factors and how do they relate to numbers? |  |
| 2. How can I identify prime and composite numbers? |  |
| 3. What are multiples, and how do they differ from factors? |  |
| 4. What are common multiples and how are they useful? |  |
| 5. What are some basic divisibility rules to remember? |  |















