Class 8 Exam > Class 8 Notes > Mathematics Class 8- New NCERT (Ganita Prakash) > Word Problems: Proportional Reasoning-1
Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1: The monthly income of A and B is in the ratio 3 : 4. If B’s income is ₹28,000, find A’s income.
Solution:
Ratio of A : B = 3 : 4
B’s income = ₹28,000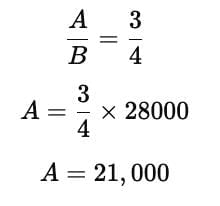
A’s income is ₹21,000.
Q2: A recipe requires flour and sugar in the ratio 5 : 2. If 1.4 kg sugar is used, how much flour is needed?
Solution:
Flour : Sugar = 5 : 2
Sugar = 1.4 kg
Q3: The ages of two friends are in the ratio 7 : 9. If the younger one is 21 years old, find the age of the elder.
Solution:
Ratio of ages = 7 : 9
Younger (7 parts) = 21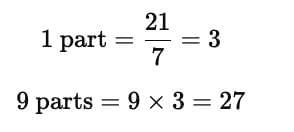
The elder friend is 27 years old.
Q3: Two numbers are in the ratio 4 : 5. If their sum is 180, find the numbers.
Solution:
Let numbers = 4x and 5x
Sum = 180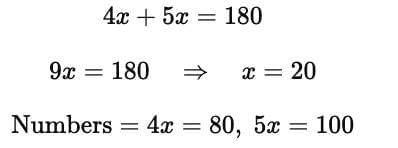
The numbers are 80 and 100.
Q4: If 8 workers can build a wall in 15 days, in how many days will 12 workers build the same wall (assuming work efficiency is same)?
Solution:
This is an inverse proportion problem.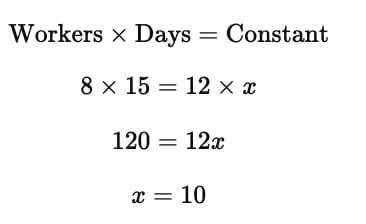
12 workers will build the wall in 10 days.
Q5: Ria and Tia share ₹840 in the ratio 4 : 3. Find each share.
Solution
Let Ria = 4x, Tia = 3x; total 4x + 3x = 840 ⇒ 7x = 840 ⇒ x = 120
Ria = 4x = ₹480, Tia = 3x = ₹360
Answer: ₹480 and ₹360
Q7: If 6 notebooks cost ₹162, how much will 14 notebooks cost?
Solution
Cost ∝ Quantity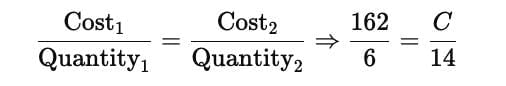
Q8: 
Q9: 
Q10:
The document Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) is a part of the Class 8 Course Mathematics Class 8- New NCERT (Ganita Prakash).
All you need of Class 8 at this link: Class 8
|
26 videos|133 docs|11 tests
|
FAQs on Word Problems: Proportional Reasoning-1 - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is proportional reasoning, and how is it applied in solving word problems? |  |
Ans. Proportional reasoning involves understanding and using ratios and proportions to solve problems. It helps in determining relationships between quantities. For instance, if a recipe requires 2 cups of flour for 4 servings, proportional reasoning allows one to calculate how much flour is needed for 10 servings by setting up a proportion: 2 cups/4 servings = x cups/10 servings. Solving this gives x = 5 cups.
| 2. How can I identify proportional relationships in word problems? | |
Ans. To identify proportional relationships, look for keywords that suggest a constant ratio, such as "for every," "per," or "in relation to." Additionally, check if altering one quantity consistently affects another in a predictable manner. For example, if a car travels 60 miles in 1 hour, it will travel 120 miles in 2 hours, indicating a proportional relationship.
| 3. What strategies can I use to solve word problems involving proportions? | |
Ans. Effective strategies include:
1. Setting up a proportion equation based on the relationship described in the problem.
2. Cross-multiplying to solve for the unknown variable.
3. Checking your answer by substituting it back into the original scenario to ensure it makes sense.
4. Using visual aids like tables or graphs to organize information.
| 4. Can you give an example of a real-life situation where proportional reasoning is useful? | |
Ans. A common real-life application of proportional reasoning is in cooking. For instance, if a dish requires 3 tablespoons of sugar for a certain number of servings, and you wish to double the recipe, you would need 6 tablespoons of sugar. This use of proportions helps maintain the flavor and consistency of the dish.
| 5. What common mistakes should I avoid when solving proportional word problems? | |
Ans. Common mistakes include:
1. Misinterpreting the relationship between quantities, leading to incorrect setups.
2. Forgetting to simplify ratios before solving, which can complicate calculations.
3. Not checking if the final answer makes sense in the context of the problem. Always ensure that the units match and that the solution aligns with the given information.
About this Document
4.61/5
Rating
Oct 09, 2025
Last updated
Related Exams
Document Description: Word Problems: Proportional Reasoning-1 for Class 8 2025 is part of Mathematics Class 8- New NCERT (Ganita Prakash) preparation.
The notes and questions for Word Problems: Proportional Reasoning-1 have been prepared according to the Class 8 exam syllabus. Information about Word Problems: Proportional Reasoning-1 covers topics
like and Word Problems: Proportional Reasoning-1 Example, for Class 8 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Word Problems: Proportional Reasoning-1.
Introduction of Word Problems: Proportional Reasoning-1 in English is available as part of our Mathematics Class 8- New NCERT (Ganita Prakash)
for Class 8 & Word Problems: Proportional Reasoning-1 in Hindi for Mathematics Class 8- New NCERT (Ganita Prakash) course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
Description
Full syllabus notes, lecture & questions for Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash) - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 8- New NCERT (Ganita Prakash) | Best notes, free PDF download
Information about Word Problems: Proportional Reasoning-1
In this doc you can find the meaning of Word Problems: Proportional Reasoning-1 defined & explained in the simplest way possible. Besides explaining types of
Word Problems: Proportional Reasoning-1 theory, EduRev gives you an ample number of questions to practice Word Problems: Proportional Reasoning-1 tests, examples and also practice Class 8
tests
Related Searches
Semester Notes
,Sample Paper
,Viva Questions
,Important questions
,Previous Year Questions with Solutions
,Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,Free
,video lectures
,mock tests for examination
,Objective type Questions
,past year papers
,study material
,Summary
,Extra Questions
,Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,MCQs
,shortcuts and tricks
,ppt
,Word Problems: Proportional Reasoning-1 | Mathematics Class 8- New NCERT (Ganita Prakash)
,Exam
,practice quizzes
;
Additional Information about Word Problems: Proportional Reasoning-1 for Class 8 Preparation
Word Problems: Proportional Reasoning-1 Free PDF Download
The Word Problems: Proportional Reasoning-1 is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Word Problems: Proportional Reasoning-1 now and kickstart your journey towards success in the Class 8 exam.
Importance of Word Problems: Proportional Reasoning-1
The importance of Word Problems: Proportional Reasoning-1 cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Word Problems: Proportional Reasoning-1 Notes
Word Problems: Proportional Reasoning-1 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Word Problems: Proportional Reasoning-1.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Word Problems: Proportional Reasoning-1 Notes on EduRev are your ultimate resource for success.
Word Problems: Proportional Reasoning-1 Class 8 Questions
The "Word Problems: Proportional Reasoning-1 Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Word Problems: Proportional Reasoning-1 on the App
Students of Class 8 can study Word Problems: Proportional Reasoning-1 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Word Problems: Proportional Reasoning-1,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Word Problems: Proportional Reasoning-1 is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup