Short Notes: A Square and A Cube | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
| Table of contents |

|
| Square Numbers |

|
| Square of Fractions and Decimal Numbers |

|
| Square Roots |

|
| Cubic Numbers |

|
| Taxicab Numbers |

|
| Cube Roots |

|
| Successive Differences of Powers |

|
Square Numbers
1. Understanding Squares
Definition: Area of a square = Side × Side.
Examples: 1² = 1, 2² = 4, 3² = 9, 4² = 16.
Squares of natural numbers = perfect squares.
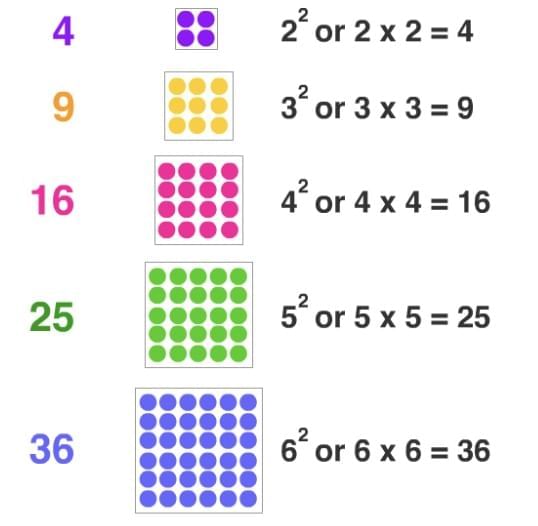
2. Notation
Square of n = n² (“n squared”).
Example: 2² = 4, 3² = 9.
Square of Fractions and Decimal Numbers
Fractions/decimals can also be squared: (2.5)² = 6.25.
1. Square of Fractions
The square of a fraction means multiplying the fraction by itself: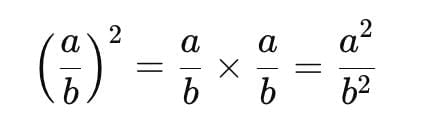
Steps to Square a Fraction
Step 1: Square the numerator – multiply the top number by itself.
Step 2: Square the denominator – multiply the bottom number by itself.
Step 3: Simplify if possible.
Examples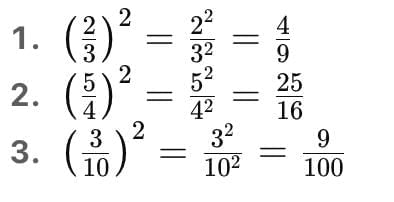
2. Square of Decimal Numbers
The square of a number is obtained by multiplying the number by itself.
Steps to Square a Decimal Number
Step 1: Ignore the decimal point
Treat the decimal number as a whole number (remove the decimal point temporarily).
Step 2: Square the number
Multiply the whole number by itself.
Step 3: Place the decimal
Count the total number of decimal places in the original number.
In the square, place the decimal point so that the number of decimal places is twice the original.
Examples
A) 0.3²
Ignore decimal and square → 3² = 9
Original decimal places = 1 → Square decimal places = 2
Answer → 0.09
B) 1.2²
Ignore decimal and square → 12² = 144
Original decimal places = 1 → Square decimal places = 2
Answer → 1.44
3. Patterns and Properties of Perfect Squares
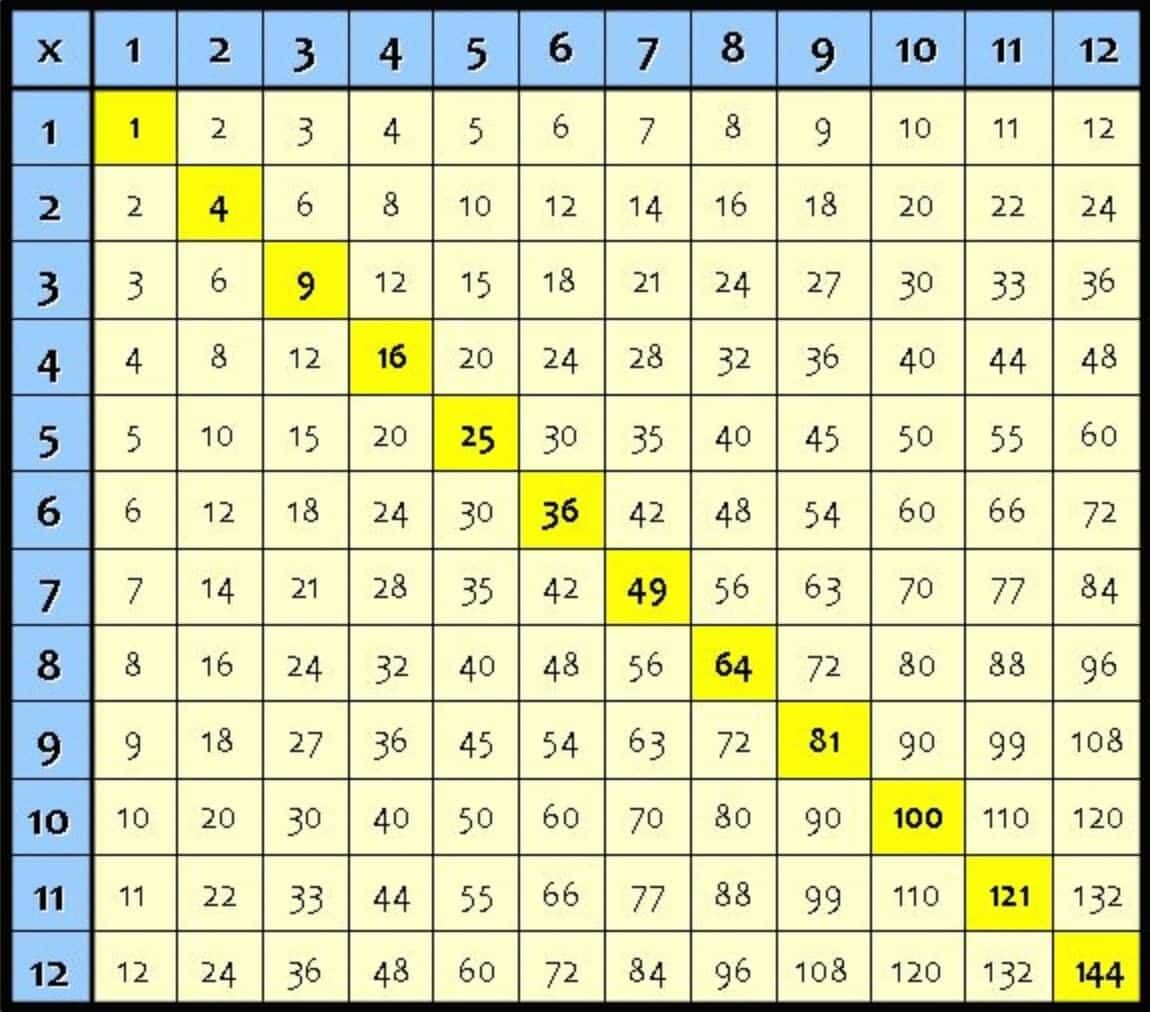
(a) Units Digit Rule
A square ends only in: 0, 1, 4, 5, 6, 9.
Never ends in: 2, 3, 7, 8.
Example: 16, 25, 49 are squares; but 23, 47 are not.
(b) Digits Pattern
Numbers ending in 1 or 9 → square ends in 1.
Numbers ending in 4 or 6 → square ends in 6.
Example: 19² = 361 (ends in 1).
(c) Zeros Rule
If number ends in n zeros, square ends in 2n zeros.
Example: 100² = 10,000 (2 zeros → 4 zeros).
(d) Parity (Even/Odd)
Square of even number = even.
Square of odd number = odd.
Example: 12² = 144 (even), 25² = 625 (odd).
(e) Odd Number Differences
Difference of consecutive squares = odd number.
2² – 1² = 3, 3² – 2² = 5, 4² – 3² = 7.
Sum of first n odd numbers = n².
(f) Perfect Square Test (Subtraction Rule)
Subtract consecutive odd numbers from n.
If result becomes 0 → number is a perfect square.
Example: 25 – 1 – 3 – 5 – 7 – 9 = 0 → 25 is a square.
(g) Finding Next Square
(n+1)² = n² + (2n+1).
Example: 35² = 1225 → 36² = 1225 + 71 = 1296.
(h) Numbers Between Squares
Between n² and (n+1)² → always 2n numbers.
Example: Between 4² = 16 and 5² = 25 → 8 numbers.
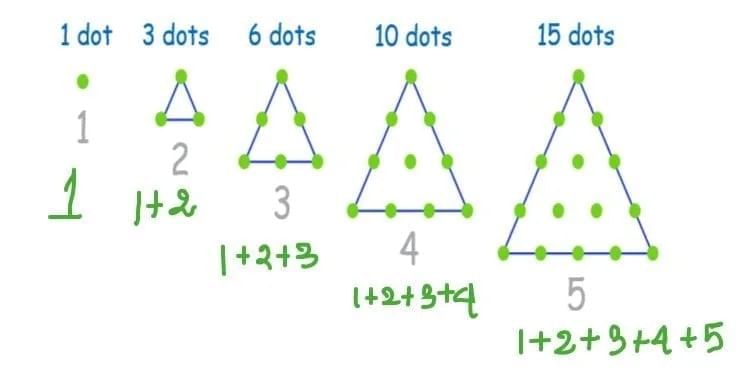
(i) Triangular Numbers Relation
Triangular numbers: 1, 3, 6, 10, 15, …
Sum of two consecutive triangular numbers = perfect square.
Square Roots
Definition
If y = x², then x = √y.
Every square root has ± values, but usually positive root is used.
Example: √49 = ±7.
Methods to Check/Find Square Roots
Listing Squares → compare with nearby perfect squares.
List squares of natural numbers:
1² = 1, 2² = 4, 3² = 9, 4² = 16, …
Compare the given number with the list of squares.
If it matches a square → the square root is the corresponding number.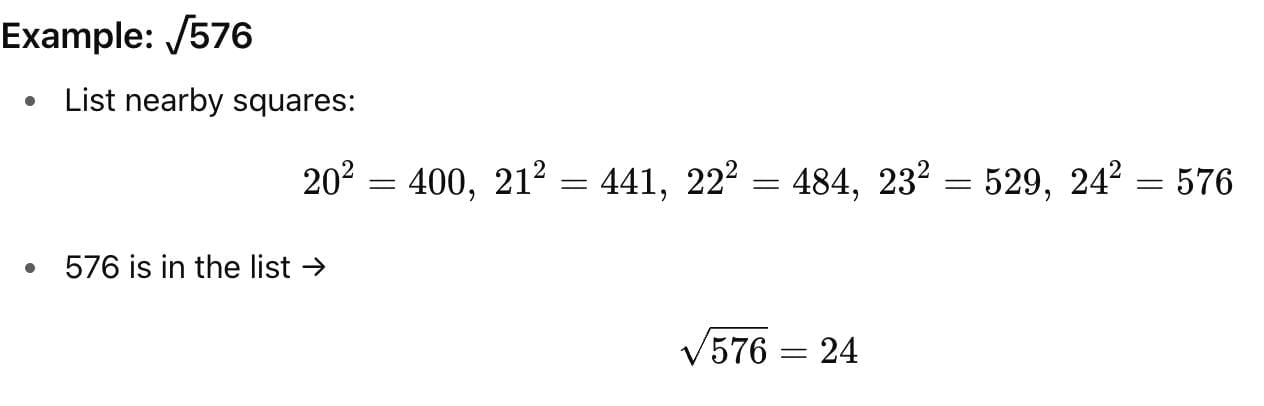 Quick Tip:
Quick Tip:
If the number is not a perfect square, it lies between the squares of two numbers → √n is between those two numbers.Successive Subtraction of Odd Numbers → subtract until 0.
– Start with the given number.
– Subtract 1, 3, 5, 7, 9… successively (odd numbers in order).
– Count how many subtractions you can do until the result becomes 0.
– The number of subtractions = the square root. Quick Tip:
Quick Tip:This method works only for perfect squares.
The sequence of odd numbers always starts from 1.
Prime Factorisation → group factors in pairs.
Example: 256 = 2⁸
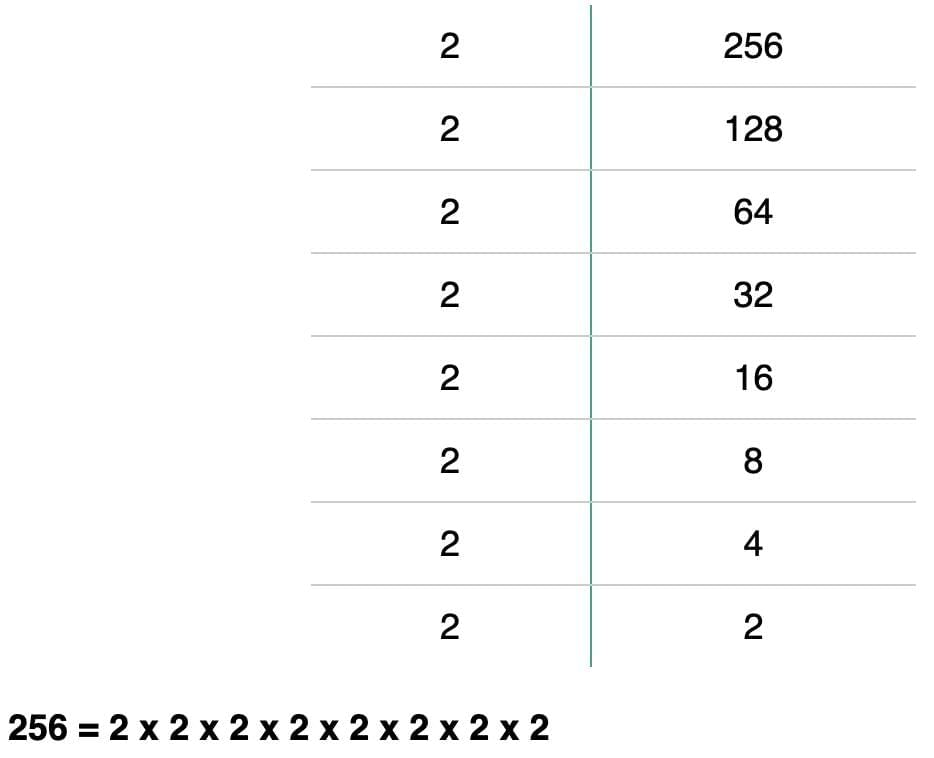 → √256 = 2⁴ = 16.
→ √256 = 2⁴ = 16.
Estimation → use nearby perfect squares.
– Identify perfect squares closest to the given number – one smaller, one larger.
– Conclude that the square root lies between the roots of these perfect squares.
– Refine by checking multiples to find the exact root (if it is a perfect square).
Quick Tip:For numbers not perfect squares, this method gives a good approximate value.
Works well with decimal approximations too.
For Non-Perfect Squares
When a number is not a perfect square, its square root can be estimated by comparing it with nearby perfect squares.
Steps:
Identify the perfect squares just below and above the number.
Conclude that the square root lies between the roots of these perfect squares.
Refine the estimate using linear approximation or trial and error.

Quick Tip:
This method gives a quick approximation.
For more precision, use long division or a calculator.
Cubic Numbers
Definition and Notation
Cube = n³ = n × n × n.
Represents volume of cube of side n.
Examples: 2³ = 8, 3³ = 27, 4³ = 64.
Properties
Cubes grow faster than squares.

Possible last digits of cubes → any digit (0–9).
Relation with Odd Numbers
n³ = sum of n consecutive odd numbers.
Example: 4³ = 13+15+17+19 = 64.
Taxicab Numbers
First discovered by Ramanujan (famous Hardy–Ramanujan number).
1729 = 1³+12³ = 9³+10³.
Smallest number expressible as sum of two cubes in two ways.
Other examples: 4104, 13832.

Cube Roots
Definition
If y = x³ → x = ³√y.
Example: ³√8 = 2.
Finding Cube Roots (Prime Factorisation)
Group factors into triplets.
Example: 3375
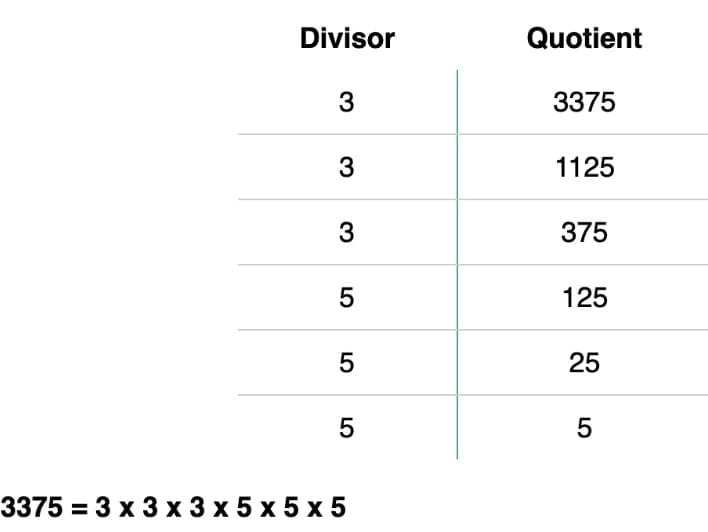 = (3×3×3)(5×5×5) → ³√3375 = 15.
= (3×3×3)(5×5×5) → ³√3375 = 15.Example: ³√8000 = 20.
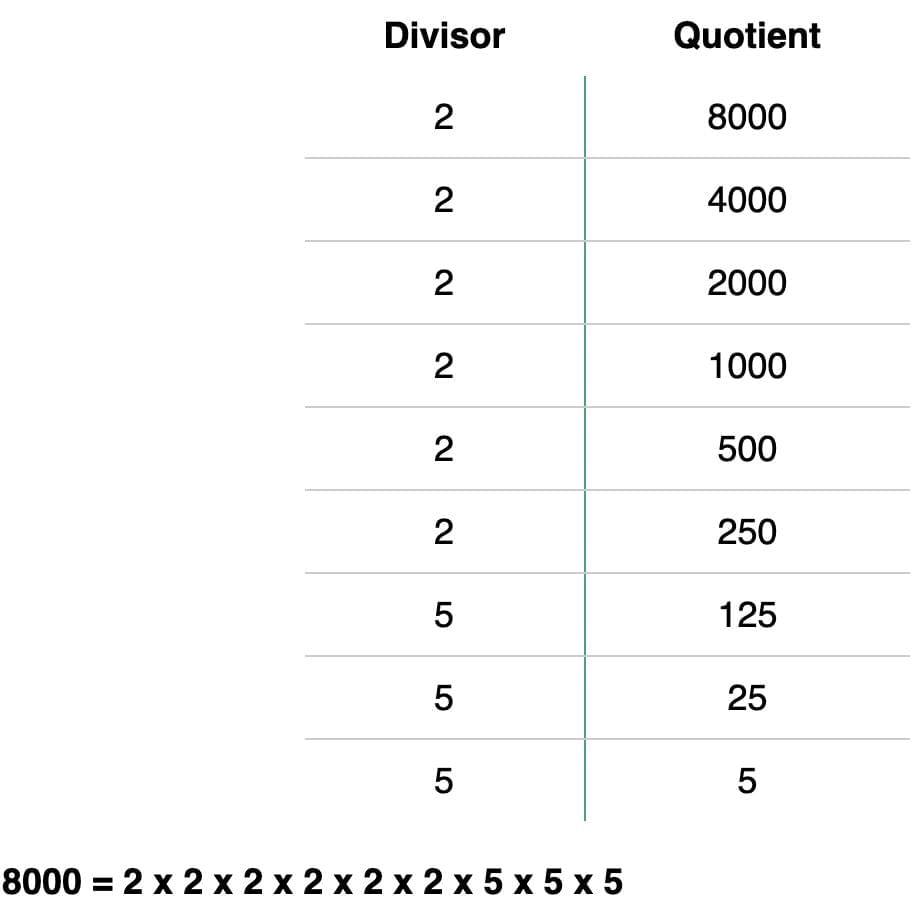 8000 = (2×2×2) (2×2×2) (5×5×5)= 2×2×2 = 20.
8000 = (2×2×2) (2×2×2) (5×5×5)= 2×2×2 = 20.
Successive Differences of Powers
When we list powers of natural numbers in order and calculate the successive differences, a pattern appears:
For squares (n²) → the second differences are constant.
For cubes (n³) → the third differences are constant.
General Rule: For nth powers, the differences become constant at the nth level.
1. Squares (n²)
Numbers:
1, 4, 9, 16, 25
First differences:
3, 5, 7, 9
Second differences:
2, 2, 2 (constant)
2. Cubes (n³)
Numbers:
1, 8, 27, 64, 125
First differences:
7, 19, 37, 61
Second differences:
12, 18, 24
Third differences:
6, 6 (constant)
General Rule
For numbers to the power 1 (linear) → first differences constant
For squares → second differences constant
For cubes → third differences constant
For nth powers → constant differences appear at nth level
|
13 videos|122 docs|11 tests
|
FAQs on Short Notes: A Square and A Cube - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is a square number and how is it calculated? |  |
| 2. How do you find the square of a fraction? |  |
| 3. Can you explain the process of squaring decimal numbers? |  |
| 4. What is a square root, and how can it be calculated? |  |
| 5. How do squares and cubes differ in mathematics? |  |




















