Short Notes: Power Play | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Exponential Notation
Definition: Shorthand for repeated multiplication of the same number.
Examples:
n² = n × n
n³ = n × n × n
n⁴ = n × n × n × n
Algebra:
a³ × b² = a × a × a × b × b
a² × b⁴ = a × a × b × b × b × b
Important Note: Addition is not exponent:
4 + 4 + 4 = 3 × 4 = 12
4 × 4 × 4 = 4³ = 64
Prime Factorization and Exponential Form
Prime factorization is expressing a number as a product of its prime numbers.
Exponential form is writing repeated prime factors using powers.
Steps to Express in Exponential Form
Find the prime factors of the number.
Group the same factors together.
Write each group as a power.
Combine to get the exponential form.
Example: Express 32,400 in exponential form
1. Prime Factorization:
32,400 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5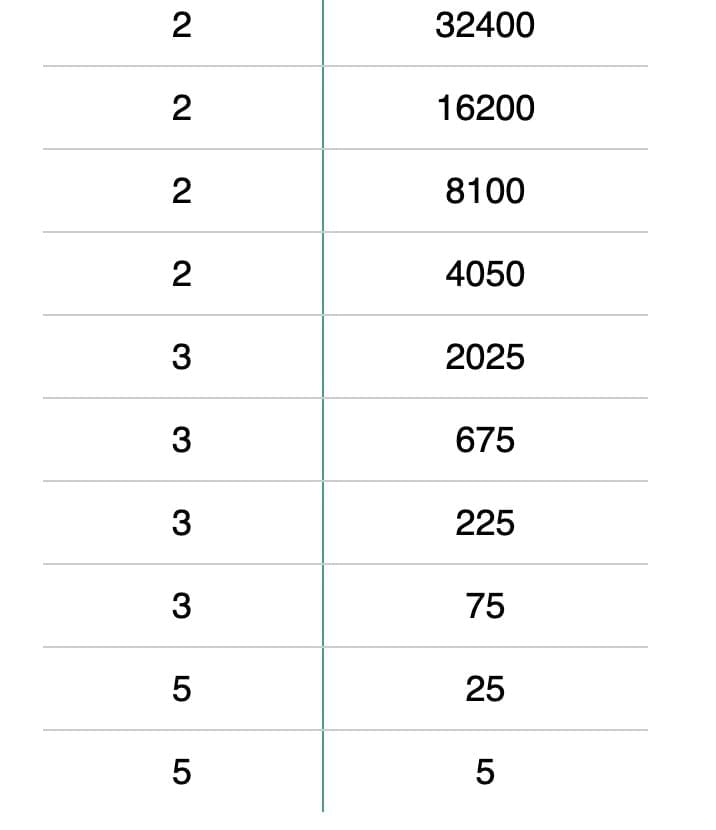
2. Group factors:
2 × 2 × 2 × 2 = 2⁴
3 × 3 × 3 × 3 = 3⁴
5 × 5 = 5²
3. Exponential Form:
32,400 = 2⁴ × 3⁴ × 5²
Quick Tip: Prime factorization is useful for finding HCF, LCM, and simplifying roots of numbers.
Laws of Exponents: Multiplication and Division of Powers
1. Multiplying Same Bases
Rule: Add the exponents
Formula: nᵃ × nᵇ = nᵃ⁺ᵇ
Example: p⁴ × p⁶ = p¹⁰
2. Power of a Power
Rule: Multiply the exponents
Formula: (nᵃ)ᵇ = nᵃ×ᵇ
Example: (2⁵)² = 2¹⁰
3. Dividing Powers with Same Base
Rule: Subtract the exponents (denominator from numerator)
Formula: nᵃ ÷ nᵇ = nᵃ⁻ᵇ, n ≠ 0
Example: 2⁴ ÷ 2³ = 2¹
4. Negative Powers
Rule: Reciprocal of the positive power
Formula: n⁻ᵃ = 1 ÷ nᵃ
Example: 3⁻² = 1 ÷ 3² = 1/9
5. Zero Exponent
Rule: Any non-zero number to the power 0 is 1
Formula: x⁰ = 1, x ≠ 0
Example: 7⁰ = 1
6. Multiplying Different Bases with Same Exponent
Rule: Multiply the bases, keep the exponent
Formula: mᵃ × nᵃ = (m × n)ᵃ
Example: 2³ × 5³ = (2 × 5)³ = 10³
7. Dividing Different Bases with Same Exponent
Rule: Divide the bases, keep the exponent
Formula: mᵃ ÷ nᵃ = (m ÷ n)ᵃ
Example: 8² ÷ 2² = (8 ÷ 2)² = 4²

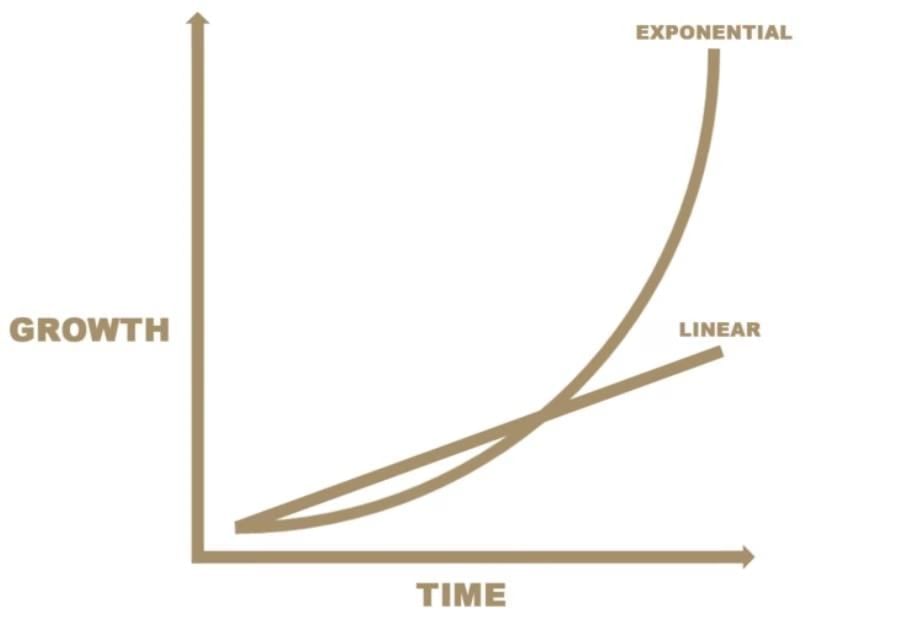
Linear vs. Exponential Growth
1. Linear Growth
Description: Adds a fixed amount per step.
Example:
Distance to the Moon: 384,400 km = 384,400,000 m
Step size: 20 cm = 0.2 m
Number of steps:
384,400,000 / 0.2 = 1,922,000,000 steps = 1.922 × 10⁹
2. Exponential Growth
Description: Multiplies by a fixed factor per step.
Example: Paper folding to the Moon:
Initial thickness: 0.001 cm
Number of folds: 46
Thickness:
T = 0.001 × 2⁴⁶ ≈ 7,036,874,841,600 cm ≈ 703,687.48 km
Powers of 10 and Scientific Notation
1. Expanded Form Using Powers of 10
For Whole Numbers:
Example: 47,561
Expanded form:
4 × 10⁴ + 7 × 10³ + 5 × 10² + 6 × 10¹ + 1 × 10⁰
For Decimals:
Example: 561.903
Expanded form:
5 × 10² + 6 × 10¹ + 1 × 10⁰ + 9 × 10⁻¹ + 0 × 10⁻² + 3 × 10⁻³
2. Scientific Notation
Any number can be written as: x × 10ʸ, where:
x = coefficient (usually between 1 and 10)
y = exponent (shows the scale of the number)
Examples:
5,900 → 5.9 × 10³
8,000,000 → 8 × 10⁶
Importance of Exponent: Determines scale; coefficient adjusts precision.

Importance of the Exponent
Exponent (y) determines the scale or magnitude of the number.
Coefficient (x) adjusts precision for significant digits.
Large Numbers in Nature
Human population (2025) = 8 × 10⁹
African elephants = 4 × 10⁵ → ~20,000 people per elephant
Grains of sand on Earth ≈ 10²¹
Stars in observable universe ≈ 2 × 10²³
Drops of water on Earth ≈ 2 × 10²⁵
Fun Fact:
10⁶ seconds ≈ 11.6 days
10⁹ seconds ≈ 31.7 years
|
20 videos|147 docs|11 tests
|
FAQs on Short Notes: Power Play - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What is exponential notation and how is it used in mathematics? |  |
| 2. How do you perform prime factorization and express it in exponential form? |  |
| 3. What are the laws of exponents for multiplication and division of powers? |  |
| 4. What is the difference between linear growth and exponential growth? |  |
| 5. How are powers of 10 used in scientific notation, and why is it important? |  |
















