Reema’s Curiosity
Ancient civilizations needed numbers to:
Count food, livestock, trade goods, ritual offerings.
Track days and seasons.
Modern numbers evolved from ancient Indian concepts:
Yajurveda Samhita lists numbers by powers of 10:
1 (eka), 10 (dasha), 100 (shata), 1000 (sahasra), 10,000 (āyuta), … up to 10¹².Indian numerals (0–9) developed ~2000 years ago.
First instance in Bakhshali manuscript (3rd century CE) with 0 as a dot.
Aryabhata (499 CE) explained calculations using the Indian system.
Transmission of Indian numerals:
To Arab world (~800 CE) via Al-Khwārizmī (On the Calculation with Hindu Numerals, 825 CE) and Al-Kindi (On the Use of Hindu Numerals, 830 CE).
To Europe (~1100 CE) and popularised by Fibonacci (~1200 CE).
Called Arabic numerals in Europe; properly Hindu or Hindu-Arabic numerals.
Key Quote:
"The ingenious method of expressing every number using ten symbols with place value emerged in India." — Laplace
Mechanism of Counting
Purpose: To determine the size of a collection of objects (e.g., counting cows).
Methods of Counting
Objects
Use sticks, pebbles, or other tokens.
Each object represents one counted item (one-to-one mapping).
Example: 5 cows → 5 sticks.

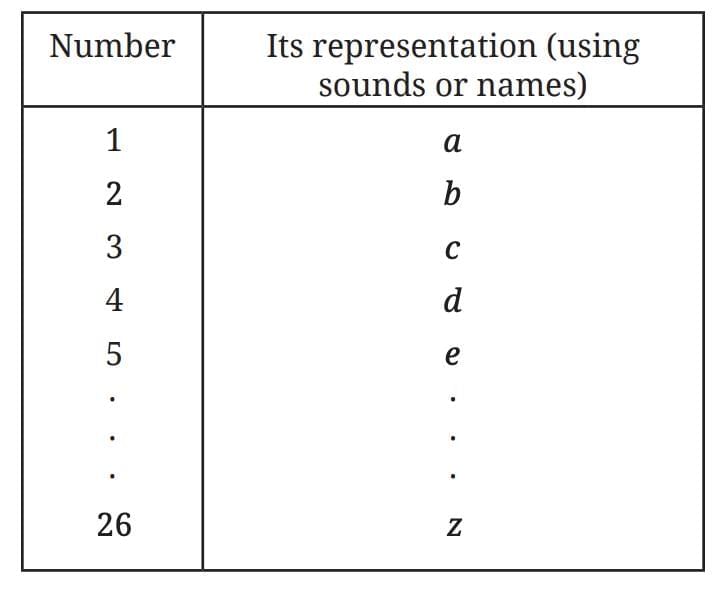
Sounds / Names
Map objects to spoken words, letters, or sounds.
Limited by the number of available symbols.
Example: “a, b, c…”
Written Symbols
Use a standard sequence of symbols to represent numbers.
This is an early form of written numbers.

Early Number Systems
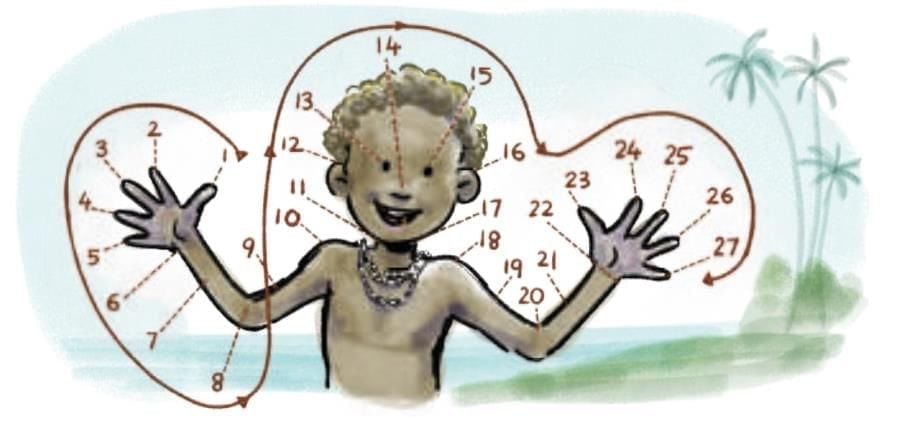
I. Body Parts
Hands, fingers, body parts used to count (e.g., Papua New Guinea).
II. Tally Marks
Marks on bones/walls (e.g., Ishango bone, 20,000–35,000 years ago; Lebombo bone, 44,000 years ago).

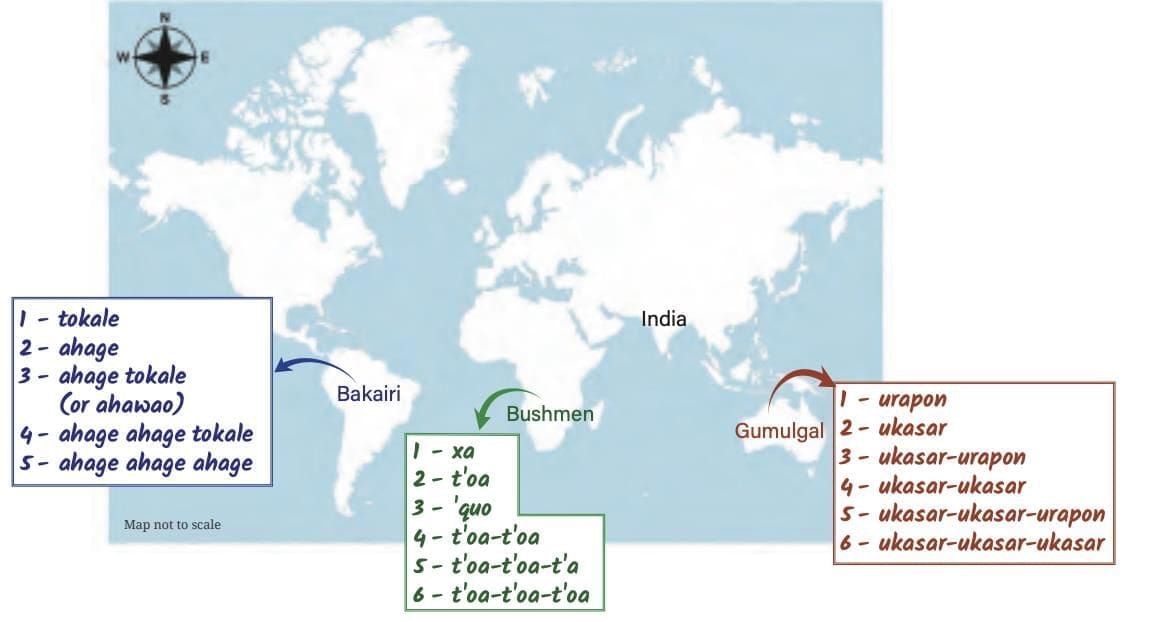
III. Counting in Groups
Example: Gumulgal (Australia) counted in 2s:
1 = urapon, 2 = ukasar, 3 = ukasar-urapon, 4 = ukasar-ukasar, …

Similar systems in South America & South Africa.
Advantage: Counting in groups reduces effort; precursor to grouping in larger systems (5s, 10s, 20s).
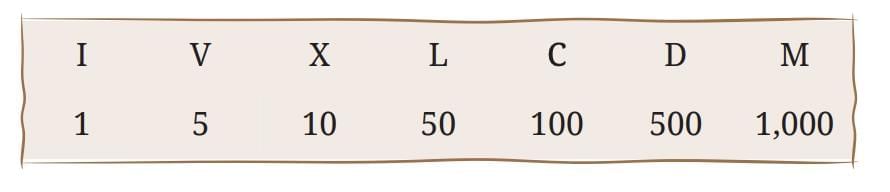
IV. Roman Numerals
Symbols: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).
Numbers represented by sums of landmark numbers (e.g., 27 = XXVII).
Efficiency: Better than tally marks but difficult for arithmetic operations.
Use of abacus for calculations.
Concept of Base
I. Egyptian Number System
Landmark numbers: 1, 10, 100, … (powers of 10, base-10 system).
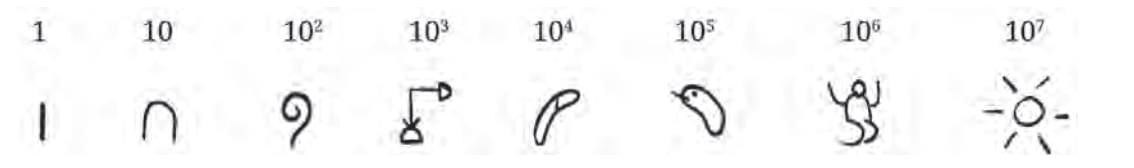
Representation: Group numbers by landmark numbers starting from the largest.
Shortcomings: Requires new symbols for higher powers of 10.
II. Base-n Systems
Landmark numbers: 1, n, n², n³, …
Example: Base-5 system → 1, 5, 25, 125, …
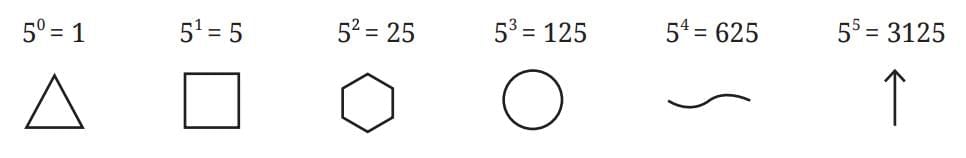
Advantages: Simplifies addition and multiplication; product of landmark numbers is another landmark number.
III. Abacus
Early calculation tool using base-10 grouping of numbers.
Counters on lines representing powers of 10.
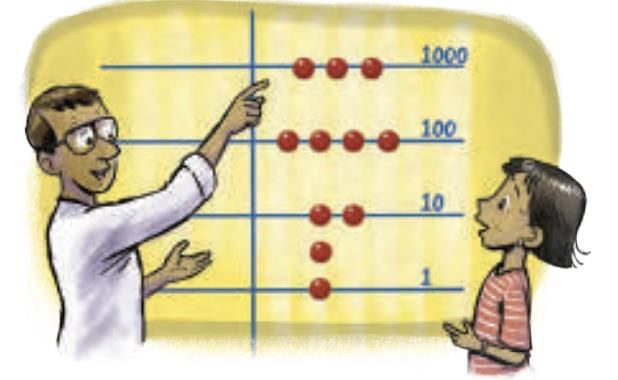
Place Value Representation
I. Mesopotamian Number System
Initially used symbols for landmark numbers.
Developed base-60 (sexagesimal) system.

Symbols: 1 and 10.
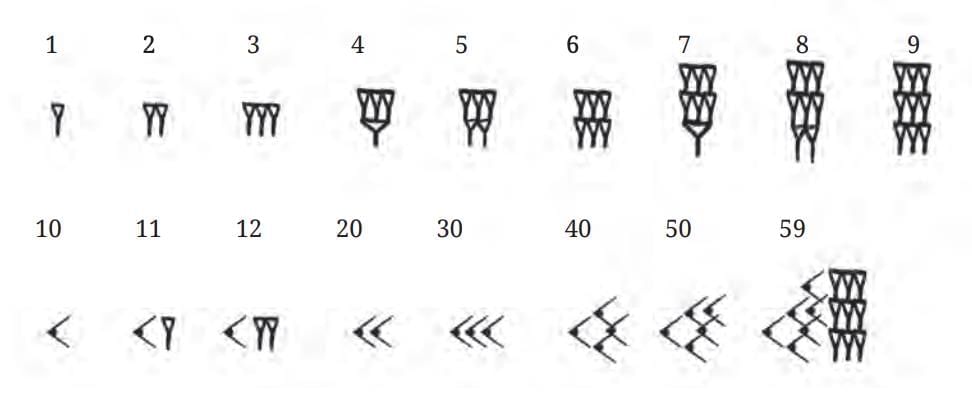
Numbers grouped by powers of 60 (e.g., 7530 = 2×3600 + 5×60 + 30).
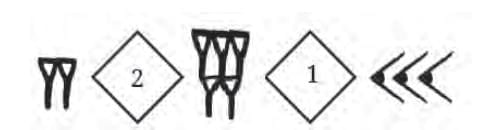
Positional system: Place of symbol determines value.
Placeholder symbol (like 0) introduced for blanks.
Influence seen in modern time measurement (60 min = 1 hour, 60 sec = 1 min).
II. Mayan Number System
Central America, 3rd–10th centuries CE.
Place value system with base-20, used placeholder for 0 (shell symbol).
Dots = 1, Bars = 5; numbers written vertically.

III. Chinese Number System
Type of System
Used rod numerals.
Decimal system (base-10).
In use from 3rd century AD.
Symbols
Separate symbols for 1–9.
Vertical position of the symbol indicates powers of 10.

Placeholders
Blank spaces used as placeholders to represent missing values.
This is similar to the Hindu number system.
Significance
Early use of positional notation.
Enabled representation of large numbers efficiently.
IV. Hindu Number System
Base-10 system
Also called the decimal system.
Uses place value to represent numbers.

Symbols / Digits
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Use of Zero (0)
Used both as a digit and as a number.
Introduced around 200 BCE.
Codified by Aryabhata and Brahmagupta.
Advantages
Allows unambiguous representation of numbers.
Facilitates arithmetic operations like addition, subtraction, multiplication, and division.
Significance
Foundation for modern mathematics including algebra, analysis, and computational methods.






















