Case Based Questions: Number Play | Mathematics for Class 6 PDF Download
Q1: Read the source and answer the question that follows
The concept of palindromic numbers involves numbers that read the same forwards and backwards. Examples of such numbers include 121, 1331, and 12321. These numbers are symmetrical and have interesting mathematical properties. Palindromes are not just visually appealing; they also exhibit unique behaviours when manipulated through certain mathematical processes. For instance, you can create a palindrome by reversing the digits of a number and adding it to itself until a palindromic number is obtained. This process often leads to surprising results and highlights the beauty of symmetry in numbers

Q1. What is the defining characteristic of a palindromic number?
(a) It is divisible by 10.
(b) It has no repeated digits.
(c) It reads the same forwards and backwards.
(d) It is always a prime number.
Ans. Option (c) is correct.
Explanation: A palindromic number reads the same forwards and backwards.
Q.2. Which of the following is an example of a palindromic number?
(a) 123
(b) 112
(c) 1331
(d) 245
Ans. Option (c) is correct.
Explanation: 1331 is a palindromic number because it reads the same forwards and backwards.
Q3. What happens when you reverse the digits of a number and add it to itself?
(a) The result is always a prime number.
(b) The result is always a multiple of 10.
(c) You may obtain a palindromic number.
(d) The result is always larger than the original number.
Ans. Option (c) is correct.
Explanation: Reversing the digits and adding it to the original number can lead to a palindromic number.
Q4. Describe a mathematical process that can result in a palindromic number.
Ans. To create a palindromic number, you can start with any number, reverse its digits, and then add the reversed number to the original number. Repeating this process often leads to a palindromic number. For example, starting with 56, reversing the digits gives 65. Adding 56 and 65 results in 121, which is a palindrome.
Q2: Read the source and answer the question that follows
Vikram and Anjali were solving a math puzzle together. They came across a 3x3 grid where they noticed that the numbers in each row, column, and diagonal all added up to the same total. "Look, Anjali! This is called a magic square!" Vikram said. "The sum of the numbers in each row, column, and diagonal is 15."Anjali was amazed. "So, every row, column, and diagonal in this grid gives the same sum? That's incredible!"
Vikram smiled and explained, "Yes, that's the magic of this square! It’s been used for thousands of years in various cultures and is a special type of puzzle."
They both started testing other grids, but only this one met the magic sum rule:
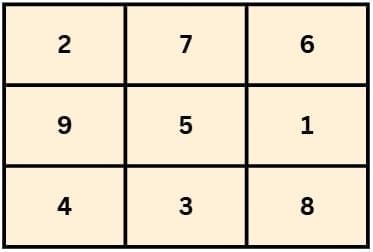
"Each row, column, and diagonal adds up to 15!" Anjali said, impressed.
Questions Based on the Story:
Q1. What is the defining feature of a magic square?
(a) The sum of numbers in each row, column, and diagonal is the same.
(b) The numbers are all prime numbers.
(c) The numbers are all even.
(d) The numbers follow a pattern of consecutive numbers.
Ans: (a) The sum of numbers in each row, column, and diagonal is the same.
Q2. In the magic square shown in the story, what is the magic sum?
(a) 10
(b) 15
(c) 20
(d) 25
Ans: (b) 15
Q3. If a grid does not follow the magic sum rule, what can we say about it?
(a) It is a valid magic square.
(b) It is a regular grid.
(c) It is not a magic square.
(d) It is a half-magic square.
Ans: (c) It is not a magic square.
Q4. Why is the magic square puzzle considered special?
Ans: It is special because the sum of the numbers in every row, every column, and both diagonals is the same, making it a unique and fascinating mathematical pattern.
Q3: Read the source and answer the question that follows
Ravi and Priya were sitting in their classroom when their teacher asked them to solve a number puzzle. The teacher gave them a set of numbers: 1, 3, 5, 7, and 9, and asked them to find out if it's possible to sum up five odd numbers to make 30.Ravi started adding the numbers:
3 + 5 + 7 + 9 = 24.
But no matter how much he tried, he couldn't make 30. Priya quickly explained, "The sum of an odd number of odd numbers will always be odd, and since 30 is an even number, it's impossible to sum five odd numbers to get 30."
Ravi was curious, so Priya continued, "When we add two odd numbers, the result is always even. But if we add an odd number of odd numbers, the result is always odd
Q1. What happens when you add two odd numbers?
(a) The result is always odd.
(b) The result is always even.
(c) The result is always zero.
(d) The result is always prime.
Ans: (b) The result is always even.
Q2. Can you sum five odd numbers to get 30?
(a) Yes, it is possible.
(b) No, it is not possible.
(c) Yes, but only when the numbers are large.
(d) It depends on the numbers chosen.
Ans: (b) No, it is not possible.
Q3. If you sum three odd numbers, what will the result be?
(a) Odd
(b) Even
(c) Prime
(d) Divisible by 5
Ans: (a) Odd
Q4. Explain why the sum of an odd number of odd numbers is always odd.
Ans: The sum of an odd number of odd numbers is always odd because when two odd numbers are added, the result is even, but adding another odd number makes the sum odd again.
|
52 videos|374 docs|23 tests
|
FAQs on Case Based Questions: Number Play - Mathematics for Class 6
| 1. What is the importance of number play in mathematics for Class 6 students? |  |
| 2. How can students improve their skills in number play? |  |
| 3. What are some effective games for practicing number play in Class 6? |  |
| 4. How do number patterns help in understanding mathematics better? |  |
| 5. What role does visualization play in number play for Class 6 students? |  |
















