Worksheet Solutions: गणित में पैटर्न | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

अधिगम पैटर्न

प्रश्न 1: खोए हुए संख्याओं को खोजें और प्रत्येक बॉक्स के लिए पैटर्न नियम का पता लगाएं।

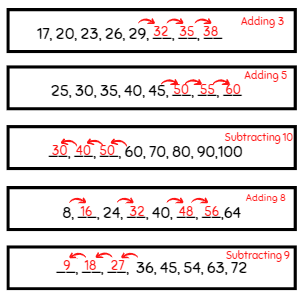
प्रश्न 2: यह पता करें कि दिए गए आरेख द्वारा किस प्रकार का पैटर्न दर्शाया गया है और उसके लिए संख्या पैटर्न लिखें।

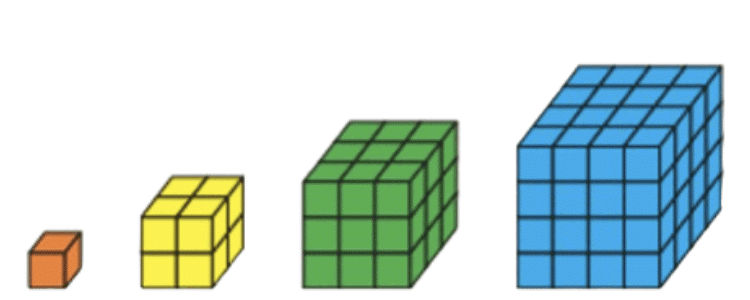
उत्तर: दर्शाया गया पैटर्न घन संख्याओं का है। संख्या पैटर्न है 1, 8, 27, 64, ... और इसी तरह।

प्रश्न 3: यह पता करें कि दिए गए आरेख द्वारा किस प्रकार का पैटर्न दर्शाया गया है और उसके लिए संख्या पैटर्न लिखें।

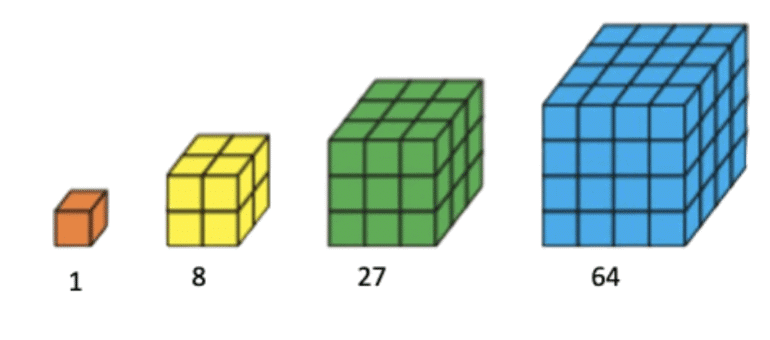
उत्तर: दर्शाया गया पैटर्न विषम संख्याओं का है। संख्या पैटर्न है 1, 3, 5, 7, 9, 11 ... और इसी तरह।

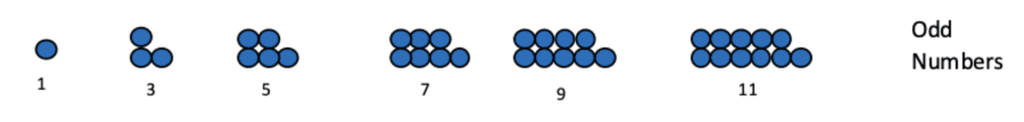
खाली स्थान भरें

प्रश्न 1: एक ________ बहुभुज वह आकृति है जिसमें सभी भुजाएँ और कोण समान होते हैं। उत्तर: नियमित

ज्यामिति में "नियमित" शब्द का अर्थ है कि बहुभुज की सभी भुजाएँ और कोण समान होते हैं।

प्रश्न 2: अनुक्रम 1, 8, 27, 64, ... ________ संख्याओं का प्रतिनिधित्व करता है। उत्तर: घन

ये संख्याएँ प्राकृतिक संख्याओं के घन हैं: 1³, 2³, 3³, 4³, .........

प्रश्न 3: ________ संख्याएँ ऐसे बिंदुओं के रूप में दर्शाई जा सकती हैं जो एक पूर्ण वर्ग बनाते हैं। उत्तर: वर्ग

वर्ग संख्याओं को बिंदुओं को एक ग्रिड में व्यवस्थित करके देखा जा सकता है जहाँ पंक्तियों की संख्या स्तंभों की संख्या के समान होती है।

प्रश्न 4: पैटर्न 2, 4, 6, 8, 10, ... ________ संख्याओं का अनुक्रम है। उत्तर: सम

यह अनुक्रम पिछले संख्या में 2 जोड़कर बनाया गया है, जिससे सम संख्याओं का अनुक्रम बनता है।

प्रश्न 5: ________ संख्याएँ हर बार समान मात्रा में बढ़ती हैं, और इस अनुक्रम को गिनती संख्याएँ कहा जाता है। उत्तर: प्राकृतिक

प्राकृतिक या गिनती संख्याएँ हर बार 1 से बढ़ती हैं: 1, 2, 3, 4, ...

सत्य या असत्य

प्रश्न 1: अनुक्रम 1, 4, 9, 16, 25, ... घन संख्याओं का उदाहरण है। उत्तर: असत्य

यह अनुक्रम वर्ग संख्याओं का उदाहरण है, न कि घन संख्याओं का।

प्रश्न 2: एक नियमित पंचकोण में समान भुजाएँ होती हैं लेकिन कोण भिन्न होते हैं। उत्तर: असत्य

एक नियमित पंचकोण में समान भुजाएँ और समान कोण दोनों होते हैं।

प्रश्न 3: विषम संख्याओं का अनुक्रम 1, 3, 5, 7, ... से शुरू होता है। उत्तर: सत्य

विषम संख्याओं का अनुक्रम 1 से शुरू होता है और प्रत्येक बार 2 से बढ़ता है।

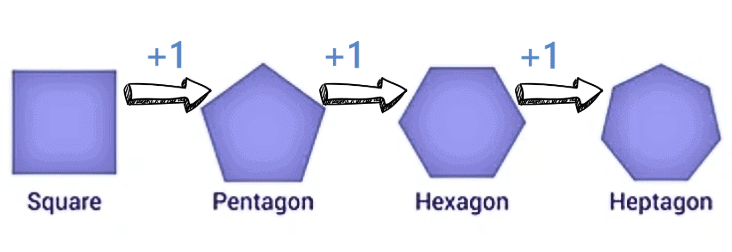
प्रश्न 4: एक आकृति अनुक्रम जो एक वर्ग से शुरू होता है और हर बार एक भुजा जोड़ता है, वह बढ़ते हुए भुजाओं वाली बहुभुजाएँ बनाएगा। उत्तर: सत्य

यह अनुक्रम एक वर्ग (4 भुजाएँ) से शुरू होगा, फिर एक पंचकोण (5 भुजाएँ), और इसी तरह, हर बार एक और भुजा जोड़ते हुए।

प्रश्न 5: संख्या 36 एक वर्ग संख्या और त्रिकोणीय संख्या दोनों हो सकती है। उत्तर: सत्य

संख्या 36 अद्वितीय है क्योंकि इसे एक वर्ग संख्या (6x6) और एक त्रिकोणीय संख्या के रूप में प्रदर्शित किया जा सकता है।

शब्द समस्या

प्रश्न 1: रिया किताबों को पिरामिड आकार में सजाने का काम कर रही है। पहली पंक्ति में 1 किताब है, दूसरी में 3, तीसरी में 6। यदि वह इस पैटर्न को जारी रखती है, तो पाँचवीं पंक्ति में कितनी किताबें होंगी?

उत्तर: प्रत्येक पंक्ति में किताबों की संख्या एक पैटर्न का पालन करती है:

• 1st row: 1
• 2nd row: 1 + 2 = 3
• 3rd row: 1 + 2 + 3 = 6
• 4th row: 1 + 2 + 3 + 4 = 10
• 5th row: 1 + 2 + 3 + 4 + 5 = 15

पाँचवीं पंक्ति में 15 किताबें होंगी।

प्रश्न 2: एक शहद का छत्ता हेक्सागोनल पैटर्न का अनुसरण करता है। यदि पहली पंक्ति में 1 कोशिका है, दूसरी में 7 कोशिकाएँ हैं, और तीसरी में 19 कोशिकाएँ हैं, तो चौथी पंक्ति में कितनी कोशिकाएँ होंगी?

उत्तर: कोशिकाओं की संख्या इस पैटर्न का पालन करती है:

• 1वीं पंक्ति = 12
• 2वीं पंक्ति = 1 + 6 = 7
• 3वीं पंक्ति = 7 + 12 = 19
• 4वीं पंक्ति = 19 + 18 = 37

चौथी पंक्ति में 37 कोशिकाएँ होंगी।

प्रश्न 3: एक स्कूल की सीढ़ी एक पैटर्न का पालन करती है: पहले कदम में 2 टाइलें हैं, दूसरे में 4, तीसरे में 6। 10वें कदम पर कितनी टाइलें होंगी?

उत्तर: प्रत्येक कदम में 2 टाइलें बढ़ती हैं। अनुक्रम इस प्रकार है:

• 1वां कदम = 2
• 2वां कदम = 4
• 3वां कदम = 6
• 4वां कदम = 8…
• 10वां कदम = 2 × 10 = 20

10वें कदम में 20 टाइलें होंगी।

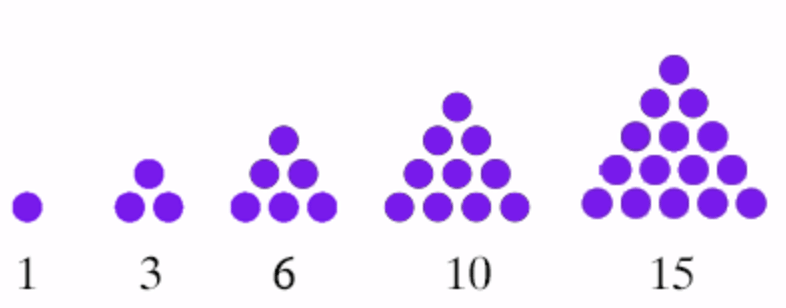
प्रश्न 4: त्रिकोणीय संख्याओं का चित्रात्मक प्रतिनिधित्व दें।

प्रश्न 5: 36 को त्रिकोणीय और वर्ग संख्याओं के रूप में प्रस्तुत करें।

उत्तर: (i) 36 को त्रिकोणीय संख्या के रूप में

(ii) 36 को वर्ग संख्या के रूप में